Другие семейства многогранников
Помимо описанных, есть и другие интересные группы многогранников.
Параллелепипеды
Кубы, четырехугольные призмы и призмы, все грани которых являются прямоугольниками, — все это частные случаи параллелепипедов, гранями которых являются попарно параллельные параллелограммы. Параллелепипеды очень популярны, так как их можно легко описать тремя векторами, выходящими из одной точки, а объем параллелепипеда рассчитывается как модуль смешанного произведения этих векторов. С помощью декартовых координат, задаваемых векторами, очень удобно проводить всевозможные вычисления, связанные с параллелепипедами.
Поликубы
Популярные фигуры полимино — это плоские фигуры, составленные из одинаковых квадратов, каждый из которых имеет по крайней мере одну общую сторону с другим. Эквивалентом полимино в пространстве являются поликубы, составленные из одинаковых кубов, каждый из которых имеет по крайней мере одну общую грань с другим. Ярким примером поликубов является с конструктор Lego. Аналогично поликубам можно построить политетраэдры, полиоктаэдры и т. д.
Многогранники, обладающие особыми свойствами
Особый интерес представляют описание и классификация семейств многогранников, обладающих каким-либо общим свойством, но необязательно всеми свойствами правильных многогранников. Так, изучаются выпуклые многогранники, все грани которых являются правильными многоугольниками (всего таких многогранников 92. их открыли Норман Джонсон и Виктор Залгаллер).
|
|
|
В этой группе насчитывается 14 многогранников, получаемых рассечением правильных многогранников и архимедовых тел, еще 15 получаются объединением правильных многогранников или архимедовых тел с 14 многогранниками из первой группы, 26 образуются путем объединения предыдущих многогранников с правильными призмам, 11 образуются при сочетании предыдущих с правильными антипризмами, а 8 являются особыми случаями расположения треугольников, квадратов, пятиугольников и шестиугольников в пространстве. Остальные многогранники этой группы представляют собой сочетания двух или трех многогранников, описанных выше.
Также существует группа многогранников, все грани которых равны, группа выпуклых многогранников, во всех вершинах которых сходится одинаковое число ребер, и многие другие. Например, если к правильной пятиугольной антипризме, приклеить к основанию правильную пятиугольную пирамиду: такой многогранник имеет десять граней в форме равносторонних треугольников и пятиугольное основание. Следовательно, это многоугольник с правильными гранями, однако в его вершинах сходится разное число ребер.
|
|
|
Зоноэдры
Зоноэдр — это выпуклый многогранник, каждая грань которого обладает той же симметрией, что и параллелограмм. Представьте себе многогранник, гранями которого являются, например, параллелограммы.
Трапецоэдры
Трапецоэдры образуются при соединении центров граней антипризм.
Ортогональные многогранники
Все их грани образуют между собой углы в 90°, а их ребра параллельны одной из трех осей декартовой системы координат. Среди выпуклых многогранников этому условию соответствуют только призмы, а среди невыпуклых — и многие другие фигуры (например, поликубы).
Производные многогранники
Соединив определенные точки любого многогранника, можно получить новый многогранник. Если мы рассечем исходный многогранник плоскостями, получим новый класс усеченных многогранников. Если разъединить грани многогранника и заполнить полученные пустоты треугольниками, образуются новые фигуры.
Неправильные многогранники
Если не заострять внимание только на правильных многогранниках, то перед нами откроется настоящая бездна. Мир невыпуклых многогранников скрывает еще больше тайн. Например, существуют многогранники с отверстиями: так, если рассматривать поликубы, то можно составить кольцо из семи и восьми маленьких кубиков, объединенных между собой. Есть и еще более сложные случаи — например, тела, в которых плоские многоугольные грани заменены пространственными многоугольниками или линейчатыми поверхностями либо к ним применены топологические деформации. На многочисленных интернет-сайтах, посвященных многогранникам, можно найти множество их классификаций и бесконечное число задач, ожидающих решения.
|
|
|
Три особых многогранника
Куб с шестью квадратными гранями, коробка, образованная шестью прямоугольниками, пирамида, число треугольных граней которой совпадает с числом основания, различные прямоугольные призмы — непросто найти такой многогранник, в котором хотя бы одна грань не будет повторяться как минимум трижды. Существует всего три вида таких фигур.
Удивительные пары
Трехмерное пространство может преподнести немало сюрпризов, и многогранники служат тому доказательством. Первый сюрприз заключается в том, что разные многогранники могут иметь одинаковые вершины, иными словами, положение вершин в пространстве не определяет конкретный многогранник. Эти два многогранника имеют семь совпадающих вершин, пять одинаковых граней и ребер, но при этом они не равны (один из них выпуклый, другой — нет).
|
|
|
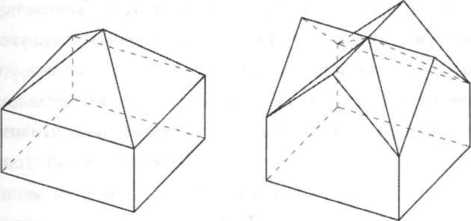Если перейти из плоскости в пространство и рассмотреть все плоскости, содержащие грани многогранника, то может ли случиться так, что одна и та же совокупность плоскостей будет определять одновременно несколько многогранников. Плоскости «пола», «стен» и «крыши» одинаковы, тем не менее определяемые ими многогранники заметно отличаются.
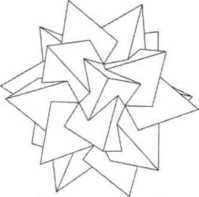
Согласно этим примерам, положение вершин и плоскостей граней не гарантирует равенства многогранников. А изменяя эти условия, мы можем получить весьма обычные фигуры.
Дата добавления: 2020-04-25; просмотров: 465; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!