Одноканальная система с градиентным алгоритмом адаптации
Цель работы: изучение свойств системы с алгоритмом адаптации, синтезированным по градиентному методу, анализ влияния темпа параметрических возмущений на качество процессов и величину управляющего воздействия.
Основные сведения
Градиентный алгоритм относится к базовым алгоритмам адаптации. Вектор градиента всегда направлен в сторону максимального локального роста функции. Следовательно, если вектор скорости настраиваемых параметров 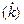 направить в сторону антиградиента
направить в сторону антиградиента 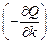 , то реализуется последовательный спуск в локальный минимум
, то реализуется последовательный спуск в локальный минимум
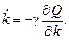 (3.1)
(3.1)
Проведем синтез адаптивной системы для одноканального линейного объекта управления
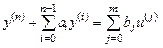 , (3.2)
, (3.2)
где u, y – управляющая и выходная переменные соответственно. Параметры объекта ai, bj точно не определены, но заданы (n + m + 1)-мер-ной областью возможных значений Wab. Операторная запись уравнения (3.2) имеет вид
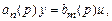 (3.3)
(3.3)
где an (p) = pn + an –1 pn –1 + …+ a0, bm (p) = bm pm + bm –1 pm -1 + … + b0,
pi = di / d ti – оператор i-кратного дифференцирования.
Цель управления зададим предельным соотношением
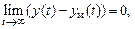 (3.4)
(3.4)
где yм(t) – эталонная траектория движения, которая удовлетворяет уравнению эталонной модели
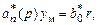 (3.5)
(3.5)
здесь 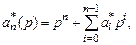 r – эталонное входное воздействие на систему. Оператор
r – эталонное входное воздействие на систему. Оператор 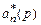 является устойчивым, т.е. корни уравнения
является устойчивым, т.е. корни уравнения 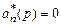 имеют отрицательную действительную часть.
имеют отрицательную действительную часть.
|
|
|
Для определения структуры «идеального» закона управления выполним преобразования уравнений (3.2) и (3.5). Вычтем из обеих частей уравнения (3.3) выражение (an (p) y):
0 = bm (p) u – an (p) y. (3.6)
Полагая y = yм, запишем уравнение (3.5)
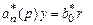 . (3.7)
. (3.7)
Прибавим к обеим частям уравнения (3.6) выражение ( 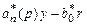 ):
):
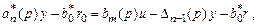 (3.8)
(3.8)
где 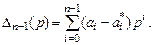 Далее вычтем из (3.8) уравнение (3.5):
Далее вычтем из (3.8) уравнение (3.5):
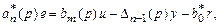 (3.9)
(3.9)
где e = y – yм. Пусть «идеальный» закон управления имеет вид
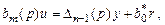 (3.10)
(3.10)
тогда
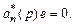 (3.11)
(3.11)
Так как полином 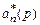 является устойчивым по условию, то e ® 0при t ® ¥, т.е. закон управления (3.10) позволяет обеспечить выполнение цели управления (3.4). Учитывая неизвестность коэффициентов поли-
является устойчивым по условию, то e ® 0при t ® ¥, т.е. закон управления (3.10) позволяет обеспечить выполнение цели управления (3.4). Учитывая неизвестность коэффициентов поли-
номов bm (p)и Dn-1(p), реальный закон управления запишем в виде
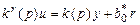 (3.12)
(3.12)
с операторами 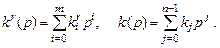
Если в процессе настройки коэффициентов регулятора (3.12) будет выполнено 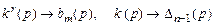 при t ® ¥, то e ®0, что показывает достижение поставленной цели управления.
при t ® ¥, то e ®0, что показывает достижение поставленной цели управления.
Для определения целевой функции введем новое рассогласование (s), которое возникает в результате замены yм на y в уравнении эталонной модели (3.5),
|
|
|
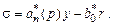 (3.13)
(3.13)
Если вычесть из (3.13) уравнение (3.5), то получим уравнение, описывающее связь между рассогласованиями e и s:
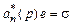 . (3.14)
. (3.14)
Из (3.14) следует, что если s ®0 при t® ¥, то в силу устойчивости 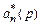 имеем e ®0при t ® ¥. Следовательно, будет выполнена поставленная цель. Это позволяет задать целевую функцию в виде
имеем e ®0при t ® ¥. Следовательно, будет выполнена поставленная цель. Это позволяет задать целевую функцию в виде
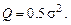 (3.15)
(3.15)
Выполним преобразования уравнения (3.13). Просуммируем уравнения объекта (3.8) и регулятора (3.12):
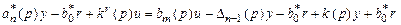 ,
,
приведем подобные и учтем (3.13):
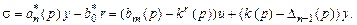 (3.16)
(3.16)
Введем обозначения для вектора неизвестных параметров
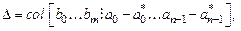
вектора настраиваемых параметров
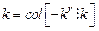
и вектора координатных переменных
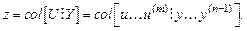
Уравнение для рассогласования (3.16) примет вид
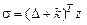 . (3.17)
. (3.17)
Алгоритм настройки коэффициентов согласно (3.1), (3.15), (3.17) имеет вид
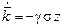 ,
,
или 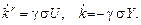
Методические указания
Объект управления имеет математическую модель вида
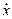 = A x + B u, y = C x, (3.18)
= A x + B u, y = C x, (3.18)
где 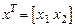 – вектор координат состояния, y – выходная переменная, u – управляющее воздействие, y, u Î
– вектор координат состояния, y – выходная переменная, u – управляющее воздействие, y, u Î 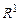 ; A, B, C – матрицы коэффициентов соответствующих размерностей;
; A, B, C – матрицы коэффициентов соответствующих размерностей;
|
|
|
A = 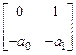 , B =
, B = 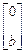 , C =
, C = 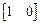 , (3.19)
, (3.19)
здесь 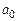 ,
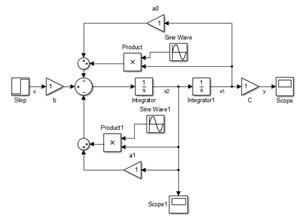
, 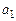 , b – неизвестные коэффициенты, которые могут быть как постоянными, так и переменными. Стационарный объект управления моделируется по схеме, изображенной на рис. 1.1, нестационарный – по схеме, представленной на рис. 1.2. Желаемое поведение системы описывают уравнения эталонной модели:
, b – неизвестные коэффициенты, которые могут быть как постоянными, так и переменными. Стационарный объект управления моделируется по схеме, изображенной на рис. 1.1, нестационарный – по схеме, представленной на рис. 1.2. Желаемое поведение системы описывают уравнения эталонной модели:
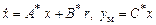 , (3.20)
, (3.20)
где r – входная переменная,
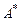 =
= 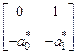 ,
, 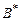 =
= 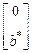 ,
, 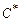 =
= 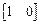 .
.
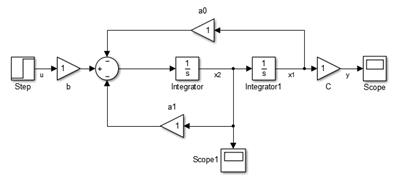
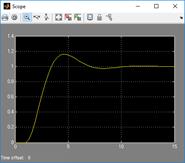
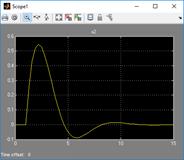
Рис. 1.1
\
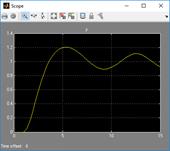
Рис. 1.2
Коэффициенты 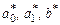 определяются по заданным показателям качества переходного процесса, приведенным в табл. 1.1, статическая ошибка работы системы допускается равной 5 %.
определяются по заданным показателям качества переходного процесса, приведенным в табл. 1.1, статическая ошибка работы системы допускается равной 5 %.
Закон управления формируется в виде
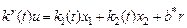 ,
,
или
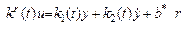 . (3.21)
. (3.21)
Т а б л и ц а 1.1
| № п/п | а0 | а1 | b |  s% s%
| t п |
| 1 | 2 | 3 | 2 | 0 | 2 |
| 2 | 1 | 4 | 1 | 10 | 4 |
| 3 | 4 | 2 | 4 | 20 | 5 |
| 4 | 4 | 1 | 4 | 0 | 4 |
| 5 | 0,1 | 0,5 | 0,1 | 30 | 10 |
| 6 | 2 | 10 | 2 | 0 | 2 |
| 7 | 10 | 2 | 10 | 0 | 5 |
| 8 | 0.5 | 1.5 | 0.5 | 5 | 3 |
Коэффициенты регулятора изменяются по градиентному алгоритму адаптации:
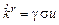 ,
,
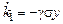 , (3.22)
, (3.22)
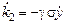 ,
,
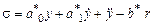 .
.
Структурная схема системы с градиентным алгоритмом адаптации (3.18)–(3.22) изображена на рис. 1.3. В данном случае предполагается «идеальное» измерение требуемых производных выходных переменных. Однако в большинстве реальных технических систем для оценки производных требуется введение наблюдателя состояния или фильтра оценки производных.
|
|
|
Уравнение асимптотического наблюдателя (идентификатора) имеет вид
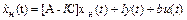
где
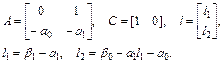
причем 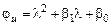 – желаемый характеристический многочлен наблюдателя, коэффициенты которого определяются, исходя из требо-
– желаемый характеристический многочлен наблюдателя, коэффициенты которого определяются, исходя из требо-
ваний к динамическим свойствам: 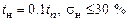 . Заметим, что
. Заметим, что
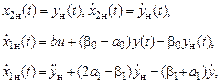
причем 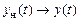 ,
, 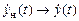 . Для старшей производной выходной переменной наблюдателя, которая является оценкой соответствующей производной выходной переменной системы, справедливо выражение
. Для старшей производной выходной переменной наблюдателя, которая является оценкой соответствующей производной выходной переменной системы, справедливо выражение
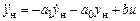 или
или 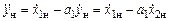 .
.
Структурная схема адаптивной системы с наблюдателем изображена на рис. 1.4.
Качество работы адаптивной системы оценить с помощью показателей: перерегулирование (s %), установившаяся ошибка ( 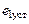 ),
),
s % = 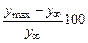 ,
, 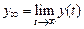 ,
, 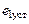 =
= 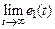 ,
,
где 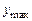 – максимальное значение выходной переменной. Оценкой быстродействия системы выбрано время переходного процесса (
– максимальное значение выходной переменной. Оценкой быстродействия системы выбрано время переходного процесса ( 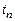 ), которое равно интервалу времени с начала работы системы до момента установления значения выходной переменной в диапазоне
), которое равно интервалу времени с начала работы системы до момента установления значения выходной переменной в диапазоне
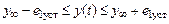 .
.
Моделирование адаптивной системы рекомендуется выполнять в среде MatLab, приложение Simulink.
Порядок выполнения работы
3.1. Определить элементы матриц 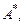
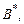
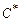 по заданным требованиям к качеству процессов (см. табл. 1.1).
по заданным требованиям к качеству процессов (см. табл. 1.1).
3.2. Выполнить моделирование стационарного (см. рис. 1.1) и нестационарного (рис. 1.2, 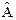 = 10,
= 10, 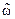 = 1) объектов, оценить устойчивость, определить показатели качества (σ %, t n).
= 1) объектов, оценить устойчивость, определить показатели качества (σ %, t n).
3.3. Собрать схему эталонной модели на интегрирующих элементах. Получить переходную характеристику (r =1(t), 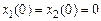 ). Определить показатели качества (σ %, t n).
). Определить показатели качества (σ %, t n).
3.4. Собрать схему адаптивной системы (3.18), (3.20)–(3.22). Параметры объекта управления приведены в табл. 1.1, схема моделирования объекта – рис. 1.1. Структурная схема адаптивной системы изображена на рис. 1.3.
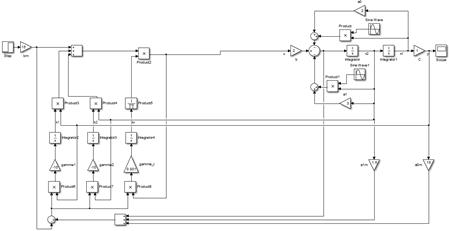
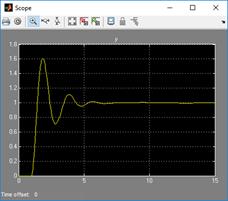
Рис. 1.3
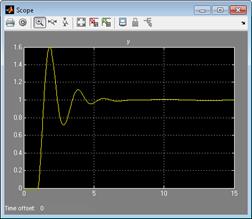
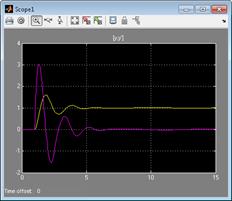
3.5. Получить графики переходной характеристики системы (y (t)), управляющего воздействия и процессов на выходе адаптора 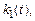
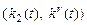 при r (t)=1(t), нулевых начальных условиях, кроме
при r (t)=1(t), нулевых начальных условиях, кроме 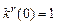 , γ = 10 в контурах настройки
, γ = 10 в контурах настройки 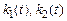 и
и 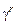 = 0.001 в контуре настройки
= 0.001 в контуре настройки 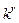 .
.
3.6. Определить показатели качества, сравнить их значения с заданными. Если качество процесса неудовлетворительное, то, изменяя γ, добиться достижения требуемых показателей.
3.7. Изменить начальные условия в объекте ( 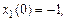
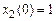 ), получить вид y (t),
), получить вид y (t), 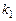 (t),
(t), 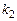 (t),
(t), 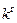 (t), u (t). Моделирование провести для различных значений g. Сравнить с результатами п. 3.5. Изобразить зависимость γ от x1(0) при γ r = 0.001 и x2(0) = 0.
(t), u (t). Моделирование провести для различных значений g. Сравнить с результатами п. 3.5. Изобразить зависимость γ от x1(0) при γ r = 0.001 и x2(0) = 0.
3.8. Изменить модель объекта управления (рис. 1.2), 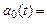
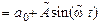 ,
, 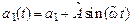 . Провести моделирование адаптивной системы при нулевых начальных условиях, кроме
. Провести моделирование адаптивной системы при нулевых начальных условиях, кроме 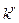 (0),
(0),
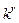 (0) = 1, и различных значениях
(0) = 1, и различных значениях 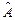 ,
, 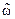 : а)
: а) 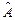 =1,
=1, 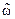 =1, б)
=1, б) 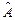 =1,
=1, 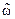 =10,
=10,
в) 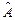 =10,
=10, 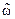 =1. Для улучшения процессов в системе изменить значе-
=1. Для улучшения процессов в системе изменить значе-
ния γ в 10 раз. Сравнить с результатами п. 3.5.
3.9 . Рассчитать параметры наблюдателя. Собрать схему системы
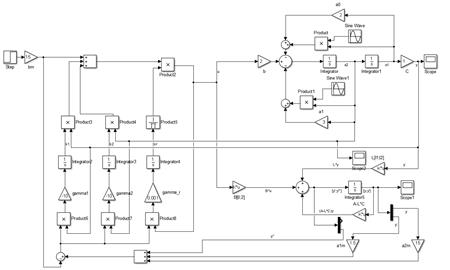
с наблюдателем (рис. 1.4). Повторить пп. 3.4, 3.8.
| |
Рис. 1.4
Содержание отчета
1. Цель работы.
2. Исходные данные.
4. Структурная схема адаптивной системы.
5. Расчет параметров адаптивного регулятора и наблюдателя.
6. Уравнения адаптивной системы с наблюдателем и вычисленными значениями параметров.
7. Графики процессов пп. 3.2–3.10, график зависимости umaxот a.
4.8. Выводы по работе.
Контрольные вопросы
1. Классификация адаптивных систем.
2. Виды эталонных моделей, способы реализации.
3. Блок-схемы беспоисковых систем с моделью.
4. Основные блоки системы с градиентным алгоритмом адаптации.
5. Влияние начальных условий в адапторе на свойства системы.
6. Уравнение адаптивного закона управления.
7. Влияние темпа параметрических возмущений на свойства системы.
8. Расчет асимптотического наблюдателя.
9. Определение вида алгоритма адаптации, использованного в лабораторной работе.
Лабораторная работа № 3
Дата добавления: 2020-04-08; просмотров: 175; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
