РАСЧЕТ СРЕДНЕЙ ДВИЖУЩЕЙ СИЛЫ МАССОПЕРЕДАЧИ. ЧИСЛО ЕДИНИЦ ПЕРЕНОСА. ВЫСОТА ЕДИНИЦЫ ПЕРЕНОСА.
Движущей силой массообменных процессов является разность между рабочей и равновесной концентрациями или наоборот. Это зависит от того, которая из указанных концентраций больше.
Движущую силу можно выражать через концентрацию распределяемого вещества в фазе G, т. е. через «Y» или в фазе «L», т. е. через «X» тогда формула. В этой связи уравнения массопередачи, записанные по фазам, имеют вид
dM=Ky•∆Y•dF•dt
dM=Kx•∆X•dF•dt
Индексы у коэффициента скорости процесса K показывают, какие концентрации приняты для выражения движущей силы. В общем случае ∆Y≠∆X и Ky≠Kx, но всегда выполняется равенство Ky•∆Y=Kx•∆X
В этой связи для всего процесса массообмена, протекающего в пределах изменения концентраций от начальных до конечных, должна быть определена средняя движущая сила по газовой фазе ∆Ym или жидкой –∆Xm
С учетом средней движущей силы процесса основное уравнение массопередачи для всей поверхности контакта фаз может быть записано в виде
; 
.
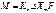При определении движущей силы возможны два случая:
– зависимость между равновесными концентрациями не линейна и определяется функциональной зависимостью самого общего вида типа Y*=f1(X);
– зависимость между равновесными концентрациями линейная – Y*=m(X)
(m– представляет собой постоянную величину).
Определим среднюю движущую силу по фазе G для случая перехода распределяемого компонента из газовой в жидкую фазу. Для элемента поверхности имеем
|
|
|
; 
.
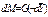Из сопоставления предыдущих равенств получим
для элементарной поверхности фазового контакта имеем
.
После интегрирования в пределах 0 –F и Yн-Yk получим
.
Изменим границы интегрирования с целью исключения отрицательного знака перед интегралом и вставим равенство для 
:
При выражении движущей силы для жидкой фазы получим аналогичное выражение:
При сравнении уравнений (1.9) и (1.10) с уравнениями (1.12) и (1.13) составим выражения для средних движущих сил по газовой и жидкой фазам:
,
.
Интегралы, стоящие в правой части равенств (1.14) и (1.15), называют числами единиц переноса – сокращенно ЧЕП.
Отсюда выражение для ЧЕП в газовой фазе имеет
а выражение для ЧЕП в жидкой фазе:
.Число единиц переноса, как следует из уравнений (1.14) и (1.15), можно определять по средней движущей силе процесса:
 |
,
.Физический смысл ЧЕП состоит в том, что эта величина характеризует изменение рабочей концентрации фазы, приходящееся на единицу движущей силы.
Числа единиц переноса выражаются интегралами, которые не могут быть решены аналитически, так как вид функции Y*=f1(X) или X*=f2(Y) в каждом конкретном случае различен. В связи с этим число единиц переноса noy и nox определяют методом графического или численного интегрирования.
|
|
|
При графическом интегрировании (рис. 1.5) задаются рядом значений y, промежуточных между величинами yн и ук.
Рис. 1.5. К расчету числа единиц переноса методом графического
интегрирования
Строят кривую зависимости 1/(y-y*) от y. Измеряют площадь, ограниченную крайними ординатами, соответствующими yk и yн, и осью абсцисс (площадь N, заштрихованная на рисунке). После этого находят величину искомого интеграла с учетом масштабов M1 и M2 осей ординат и абсцисс:
Аналогично, пользуясь графиком зависимости 1/(x-x*) от x, определяют величину nox.
Достаточно часто за основную характеристику аппарата принимают его высоту. Обозначим площадь поперечного сечения и высоту аппарата, соответственно f и H, тогда F=Hfσ. Из уравнения (1.11) после изменения пределов интегрирования и решения относительно высоты аппарата для газовой фазы получим
.
Комплекс 
имеет размерность длины [м] и физический смысл, состоящий в том, что он представляет собой высоту аппарата, эквивалентную единице переноса (ВЕП). Обозначим
, 
.
Тогда уравнения массопередачи по фазам можно записать следующим образом:
, 
.
Высота, эквивалентная единице переноса, по смыслу соответствует величине, обратной объемному коэффициенту массопередачи, а число единиц переноса – величине, обратной движущей силе процесса.
|
|
|
Чем выше интенсивность массопередачи в аппарате, тем меньше в нем величина ВЕП. Значения ВЕП определяются по эмпирическим формулам для различных типов аппаратов. Отметим также, что ВЕП используется только для расчета аппаратов с постоянным поперечным сечением рабочей части.
56) ОСНОВЫ ТЕХНОЛОГИЧЕСКОГО ПРОЕКТИРОВАНИЯ МАССООБМЕННЫХ АППАРАТОВ. РАСЧЕТ ДИАМЕТРА МАССООБМЕННЫХ АППАРАТОВ. РАСЧЕТ ДИАМЕТРА ПРОТИВОТОЧНЫХ КОЛОНН.
При технологическом расчете массообменных аппаратов должны бытьопределены их основные размеры: диаметр (для аппаратов цилиндрической формы), характеризующий производительность аппарата, и рабочая высота (длина), отражающая интенсивность протекающего в нем процесса.
Диаметр аппарата. Расчет диаметра аппарата производится по уравнению расхода:Q = Sw0,где Q — объемный расход фазы, скорость которой определяет площадь поперечного сечения аппарата, например газа — я процессе абсорбции, пара — в процессе ректификации и т. д.; w0 — фиктивная, или приведенная, скорость той же фазы, т. е. скорость, отнесенная к полному сечению аппарата; S — площадь поперечного сечения аппарата.
|
|
|
Для круглого поперечного сечения S = ПD2/4 и, следовательнооткуда диаметр аппарата. Выбор скорости необходимо осуществлять на основе следующих общих соображений. С увеличением скоростей потоков, как правило, возрастают коэффициенты массопередачи, а иногда и удельная поверхность контакта фаз (например при барботаже), в результате чего, уменьшается требуемый рабочий объем аппарата. Вместе с тем при увеличении скоростей потоков возрастает гидравлическое сопротивление аппарата, что приводит к увеличению расхода энергии на проведение процесса. Поэтому наиболее правильным является определение (на основе технико-экономических соображений) оптимальной скорости газа или пара. Технико-экономический расчет позволяет найти наивыгоднейший диаметр аппарата, при котором стоимость эксплуатации его будет наименьшей.
Однако на практике часто ограничиваются расчетом фиктивной скорости, исходя из максимального ее значения. Упрощенный подход к вычислению фиктивной скорости обусловлен тем, что во многих случаях ее предельное значение определяется наступлением «захлебывания» в против оточных аппаратах, или чрезмерным возрастанием брызгоуноса. В процессах массообмена, где повышенное гидравлическое сопротивление не имеет весьма существенного значения, например при ректификации или при абсорбции, проводимых под избыточным давлением,оптимальная скорость обычно близка к предельной и может быть, в первом приближении, принята равной скорости захлебывания, уменьшенной, например, на 10—20%.
В остальных случаях следует учитывать, что в массообменных аппаратах, по мере увеличения относительной скорости фаз, возникают различные гидродинамические режимы, отличающиеся последовательно повышающейся интенсивностью массопередачн. Поэтому выбор фиктивной скорости производят в соответствии с намечаемым гидродинамическим режимом работы аппарата, проверяя выбранную скорость по величине предельно допустимой. Указания по выбору фиктивных скоростей приведены ниже в главах, посвященных конкретным массообменным процессам.
Дата добавления: 2019-11-25; просмотров: 535; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!