Контрольные  вопросы и задания

1. Какие деформации возникают при кручении?

2. Какие гипотезы выполняются при деформации кручения?

3. Изменяются ли длина и диаметр вала после скручивания?

222                                                                                          Лекция 26

4. Какие внутренние силовые факторы возникают при кручении?

5. Что такое рациональное расположение колес на валу?

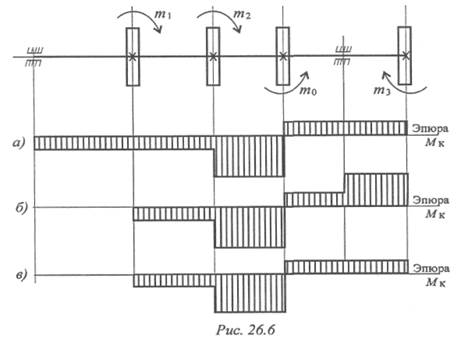
6. Для заданного вала (рис. 26.6) выбрать соответствующую
эпюру крутящих моментов (а, б, в). m 1 = 40Н•м; т 2 = 180Н•м;
m₀ = 280Н•м.

  

 

7. В каком порядке рациональнее расположить шкивы на валу
для уменьшения нагрузки на вал (рис. 26.7)?

 

     

                                                                                        Тема 2.5. Кручение                                                                                        223

ЛЕКЦИЯ 27

Тема 2.5. Кручение.

Напряжения и деформации

При кручении

Иметь представление о напряжении и деформациях при круче­нии, о моменте сопротивления при кручении.

Знать формулы для расчета напряжений в точке поперечного сечения, закон Гука при кручении.

Напряжения при кручении

Проводим на поверхности бру­са сетку из продольных и попе­речных линий и рассмотрим рису­нок, образовавшийся на поверхно­сти после деформации (рис. 27.1а). Поперечные окружности, оставаясь плоскими, поворачиваются на угол φ , продольные линии искривляют­ся, прямоугольники превращают­ся в параллелограммы. Рассмотрим элемент бруса 1234 после деформа­ции.

                                   

                     

При  выводе    формул    используем    закон    Гука    при    сдвиге    и    гипотезу

224                                                                       Лекция 27

плоских сечений и неискривления радиусов поперечных сечений.

При кручении возникает напряженное состояние, называемое «чистый сдвиг» (рис. 27.16).

При сдвиге на боковой поверхности элемента 1234 возникают касательные напряжения, равные по величине (рис. 27.1в), элемент деформируется (рис. 27.1г).

Материал подчиняется закону Гука. Касательное напряжение пропорционально углу сдвига.

Закон Гука при сдвиге τ = Gγ ,

G — модуль упругости при сдвиге, Н/мм²; γ -- угол сдвига, рад.

Напряжение в любой точке поперечного сечения

   Рассмотрим поперечное сечение круглого бруса. Под действием внешнего момента в каждой точке поперечного сечения возникают силы упругости dQ (рис. 27.2).

                                            

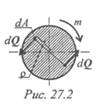
 где τ — касательное напряжение; dA — элементарная площадка.

  В силу симметрии сечения силы dQ образуют пары (см. лекцию 26).

Элементарный момент силы dQ относительно центра круга

       

где р — расстояние от точки до центра круга.

Суммарный момент сил упругости получаем сложением (интегрированием) элементарных моментов:

         

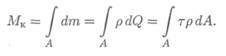
После преобразования получим формулу для определения напря­жений в точке поперечного сечения:

         

            Тема 2.5. Кручение                                                   225

При ρ = 0 τ_к = 0; касательное напряжение при кручении про­порционально расстоянию от точки до центра сечения. Полученный интеграл J_p (лекция 25) называется полярным моментом инерции сечения. J_p является геометрической характеристикой сечения при кручении. Она характеризует сопротивление сечения скручиванию.

Анализ полученной формулы для J_p показывает, что слои, рас­положенные дальше от центра, испытывают большие напряжения.

Эпюра распределения касательных напряжений при кручении (рис. 27.3)

   

---

Дата добавления: 2019-09-13; просмотров: 2454; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!