Внутренние силовые факторы при кручении.

Построение эпюр крутящих моментов

Иметь представление о деформациях при кручении, о внутрен них силовых факторах при кручении.

Уметь строить эпюры крутящих моментов.

Деформации при кручении

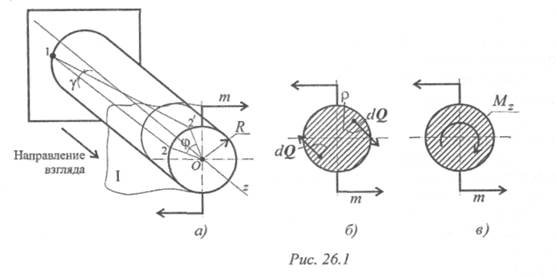
Кручение круглого бруса происходит при нагружении его парами сил с моментами в плоскостях, перпендикулярных продольной оси. При этом образующие бруса искривляются и разворачиваются на угол γ называемый углом сдвига (угол поворота образующей). Поперечные сечения разворачиваются на угол φ , называемый углом закручивания (угол поворота сечения, рис. 26.1).

Длина бруса и размеры поперечного сечения при кручении не изменяются.

Тема 2.5. Кручение. Внутренние силовые факторы при кручении 217

Связь между угловыми деформациями определяется соотношением

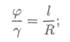l— длина бруса; R — радиус сечения.

Длина бруса значительно больше радиуса сечения, следовательно, φ » γ.

Угловые деформации при кручении рассчитываются в радианах.

Гипотезы при кручении

1. Выполняется гипотеза плоских сечений: поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.

2. Радиус, проведенный из центра поперечного сечения бруса, после деформации остается прямой линией (не искривляется).

3. Расстояние между поперечными сечениями после деформации не меняется. Ось бруса не искривляется, диаметры поперечных сечений не меняются.

Внутренние силовые факторы при кручении

Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — крутящий момент.

Внешними нагрузками также являются две противоположно направленные пары сил.

Рассмотрим внутренние силовые факторы при кручении круглого бруса (рис. 26.1).

Для этого рассечем брус плоскостью I и рассмотрим равновесие отсеченной части (рис. 26.1а). Сечение рассматриваем со стороны отброшенной части.

Внешний момент пары сил разворачивает участок бруса против часовой стрелки, внутренние силы упругости сопротивляются повороту. В каждой точке сечения возникает поперечная сила dQ (рис. 26.16). Каждая точка сечения имеет симметричную, где возникает поперечная сила, направленная в обратную сторону. Эти силы образуют пару с моментом dm = pdQ ; p — расстояние от точки

218 Лекция 26

до центра сечения. Сумма поперечных сил в сечении равна нулю: . ΣdQ = 0.

С помощью интегрирования получим суммарный момент сил упругости, называемый крутящим моментом:

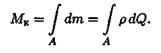
Практически крутящий момент определяется из условия равновесия отсеченной части бруса.

Крутящий момент в сечении равен сумме моментов внешних сил, действующих на отсеченную часть (рис. 26.1в):

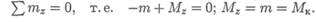
Эпюры крутящих моментов

Крутящие моменты могут меняться вдоль оси бруса. После определения величин моментов по сечениям строим график-эпюру крутящих моментов вдоль оси бруса.

Крутящий момент считаем положительным, если моменты внешних пар сил направлены по часовой стрелке, в этом случае момент внутренних сил упругости направлен против часовой стрелки (рис. 26.2).

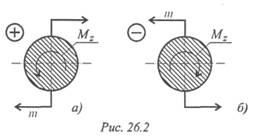
Порядок построения эпюры моментов аналогичен построению эпюр продольных сил. Ось эпюры параллельна оси бруса, значения моментов откладывают от оси вверх или вниз, масштаб построения выдерживать обязательно.

Примеры решения задач

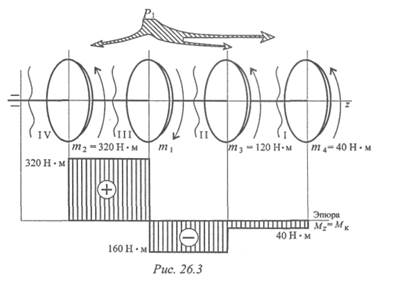
Пример 1. На распределительном валу (рис. 26.3) установлены четыре шкива, на вал через шкив 1 подается мощность 12 кВт, которая через шкивы 2, 3, 4 передается потребителю; мощности распределяются следующим образом: Р2 = 8 кВт , Рз = 3 кВт , Р4 = 1кВт ,

Тема 2.5. Кручение. Внутренние силовые факторы при кручении 219

вал вращается с постоянной скоростью ώ = 25 рад/с. Построить эпюру крутящих моментов на валу.

Решение

1. Определяем моменты пар сил на шкивах. Вращающий момент определяем из формулы мощности при вращательном движении

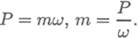
Момент на шкиве1 движущий, а моменты на шкивах 2, 3, 4 — моменты сопротивления механизмов, поэтому они имеют противоположное направление. Брус скручивается между движущим моментом и моментами сопротивления. При равновесии момент движущий равен сумме моментов сопротивления:

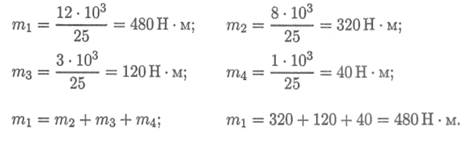
220 Лекция 26

2. Определяем крутящие моменты в поперечных сечениях бруса
с помощью метода сечений.

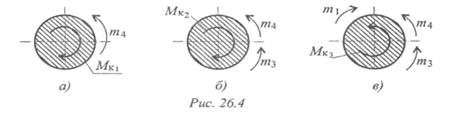
Сечение I (рис. 26.4а):

- m4 + М_К₁ = 0; М_К1 = m4; М_К ₁ = 40Н • м — крутящий момент отрицательный.

Сечение II (рис. 26.4b):

- m4 – т ₃ + М_К2 = 0; М_К2 = m4 + m3; М_К2 = 40 + 120 = 160Н•м — крутящий момент отрицательный.

Сечение III (рис. 26.4в):

- m4 – т ₃ + т 1 — М_кз = 0; -М_кз = m4 + т ₃ - т 1;

-М_кз = 40 + 120 - 480; М_Кз = 320 Н • м — крутящий момент положительный.

Сечение IV :

M_K ₄ = - m4 – т ₃ + т 1 – т ₂= 0.

3. Строим эпюру крутящих моментов. Заметим, что скачок на
эпюре всегда численно равен приложенному вращающему моменту.

Выбираем соответствующий масштаб.

Откладываем значения моментов, штрихуем эпюру поперек, обводим по контуру, записываем значения моментов (см. эпюру под схемой вала (рис. 26.3)). Максимальный крутящий момент на участке IIIМкз =320Н•м.

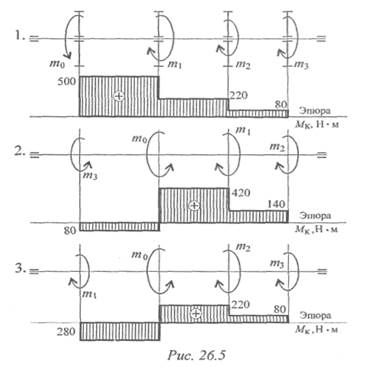
Пример 2. Выбрать рациональное расположение колес на валу (рис. 26.5). т 1= 280 Н • м; т₂ = 140 Н • м; т₃ = 80 Н • м.

Примечание. Меняя местами колеса (шкивы) на валу, можно изменять величины крутящих моментов. Рациональным расположением является такое, при котором крутящие моменты принимают минимальные из возможных значения.

m0 = т ₁ + т 2 + т ₃= 280 + 140 + 80 = 500 Н • M.

Тема 2.5. Кручение. Внутренние силовые факторы при кручении 221

Рассмотрим нагрузки на валу при различном расположении колес.

Из представленных вариантов наиболее рационально расположение шкивов в третьем случае, здесь значения крутящих моментов минимальны. Вывод: при установке шкивов желательно, чтобы мощность подавалась в середине вала и по возможности равномерно распределялась направо и налево.

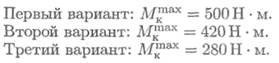
Дата добавления: 2019-09-13; просмотров: 693; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 35 36 37 38 394041 42 43 44 Следующая ⇒

Мы поможем в написании ваших работ!