Контрольные вопросы и задания

⇐ ПредыдущаяСтр 38 из 64Следующая ⇒

1. Какие внутренние силовые факторы возникают при сдвиге и
смятии?

2. Сформулируйте закон парности касательных напряжений.

3. Как обозначается деформация при сдвиге?

4. Запишите закон Гука при сдвиге.

5. Какой физический смысл у модуля упругости?

6. Укажите единицы измерения напряжений сдвига и смятия и
модуля упругости.

7. Как учесть количество деталей, использованных для передачи
нагрузки при расчетах на сдвиг и смятие?

8. Запишите условия прочности на сдвиг и смятие.

9. Почему при расчете на смятие цилиндрических деталей вместо боковой цилиндрической поверхности подставляют плоскость,
проходящую через диаметр?

10. Чем отличается расчет на прочность при сдвиге односрезной
заклепки от двухсрезной?

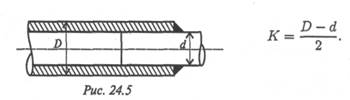
11. Запишите формулу для расчета сварного соединения.
Стержни круглого поперечного сечения сварены угловым швом
(рис. 24.5).

206 Лекция 24

12. Ответьте на вопросы тестового задания.

Тема 2.3. Практические расчеты на срез и смятие

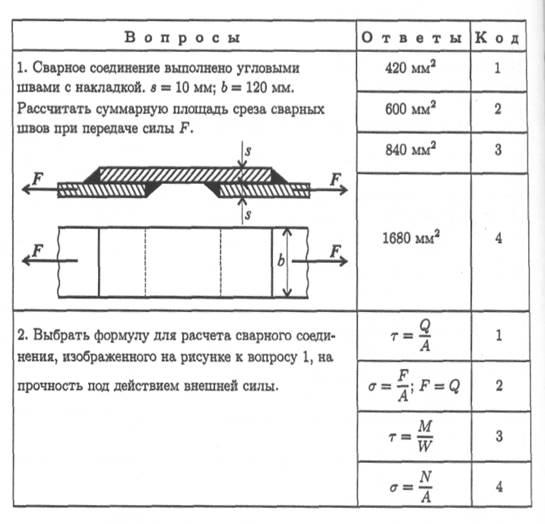
Тема 2.3. Практические расчеты на срез и смятие 207

208 Лекция 25

ЛЕКЦИЯ 25

Тема 2.4. Геометрические характеристики плоских сечений

Иметь представление о физическом смысле и порядке определения осевых, центробежных и полярных моментов инерции, о главных центральных осях и главных центральных моментах инерции.

Знать формулы моментов инерции простейших сечений, способы вычисления моментов инерции при параллельном переносе осей.

При растяжении, сжатии, смятии и сдвиге деталь сопротивляется деформации всем сечением одинаково. Здесь геометрической характеристикой сечения является площадь.

При кручении и изгибе сечение сопротивляется деформации не одинаково, при расчетах напряжений появляются другие геометрические характеристики сечения, влияющие на сопротивления сечения деформированию.

Статический момент площади сечения

Рассмотрим произвольное сечение (рис. 25.1).

Если разбить сечение на бесконечно малые площадки dA и умножить каждую площадку на расстояние до оси координат и проинтегрировать полученное выражение, получим статический момент площади сечения:

Для симметричного сечения статические моменты каждой половины площади равны по величине и имеют разный знак. Следовательно, статический момент относительно оси симметрии равен нулю.

Статический момент используется при определении положения

Тема 2.4. Геометрические характеристики плоских сечений 209

центра тяжести сечения:

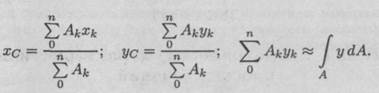
Формулы для определения положения центра тяжести можно записать в виде

Центробежный момент инерции

Центробежным моментом инерции сечения называется взятая по всей площади сумма произведений элементарных площадок на обе координаты:

Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Центробежный момент инерции относительно осей, проходящих через центр тяжести сечения, равен нулю.

Оси, относительно которых центробежный момент равен нулю, называются главными. Главные оси, проходящие через центр тяжести, называют главными центральными осями сечения.

Осевые моменты инерции

Осевым моментом инерции сечения относительно некоторой оси, лежащей в этой же плоскости, называется взятая по всей площади сумма произведений элементарных площадок на квадрат их расстояния до этой оси:

1) осевой момент инерции сечения относительно оси Ох

210 Лекция 25

Дата добавления: 2019-09-13; просмотров: 1774; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 33 34 35 36 373839 40 41 42 Следующая ⇒

Мы поможем в написании ваших работ!