Расчетно-графическая работа 2
Условие равновесия плоской системы сходящихся сил в аналитической форме
Задание. Определить реакции стержней АС иAD (рис. П1.3).
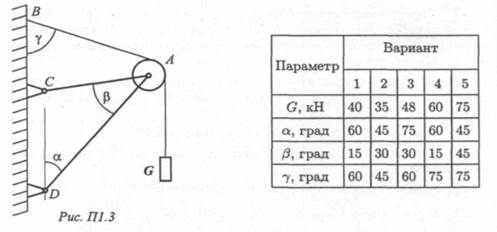
При защите работ ответить на вопросы карт с тестовыми заданиями.
Практическое занятие 1 135
Темы 1.1, 1.2. Статика.
Плоская сходящаяся система сил

136 Практическое занятие 1

 Практическое занятие 2 137
Практическое занятие 2 137
Практическое занятие 2
Тема 1.4. Плоская система произвольно
Расположенных сил
Знать теорему Пуансо о приведении силы к точке.
Уметь приводить произвольную плоскую систему сил к точке, определяя величины главного вектора и главного момента системы.
Знать три формы уравнений равновесия и уметь ими пользоваться при определении реакций в опорах балочных систем.
Основные формулы и предпосылки расчета
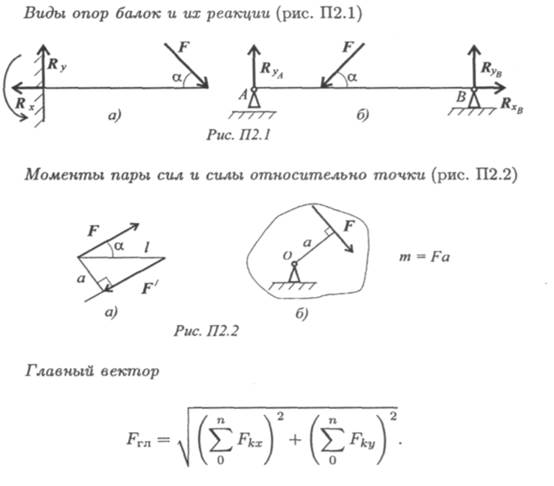
138 Практическое занятие 2
Главный момент
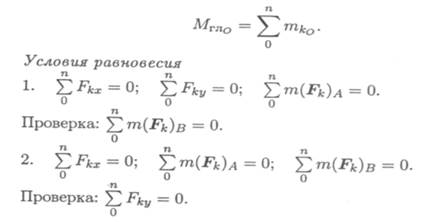
Упражнения при подготовке к самостоятельной
Работе
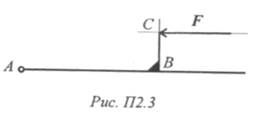
1. Перенести силу F в точку А, используя теорему Пуансон (рис. П2.3). F = 20 кН; АВ = 6 м; ВС = 2 м.
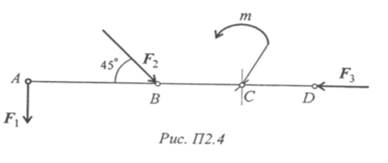
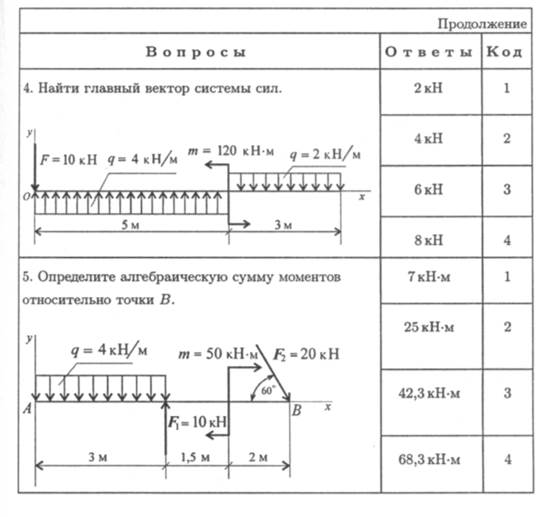
2. Привести систему сил к точке В, определить главный вектор
и главный момент системы сил (рис. П2.4). АВ = 2 м; ВС = 1,5 м;
CD = 1м. F 1 = 18 кН; F 2 = 10 кН; F3 = 30 кН; т = 36кН∙м.
Практическое занятие 2 139
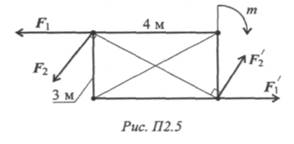
3. Система сил находится в равновесии. Определить величину
момента пары т (рис. П2.5). F 1 = F'1 = 10кН; F2 = F'2 = 20 кН.
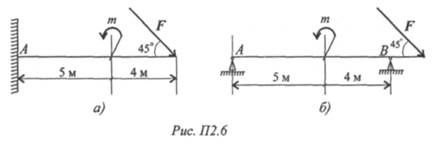
4. Нанести реакции в опорах балок 1 и 2 (рис. П2.6).
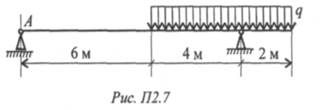
5. Определить величину реакции в опоре А. Приложена распределенная нагрузка интенсивностью q = 5кН/м (рис. П2.7).
6. Записать систему уравнений равновесия для определения реакций в опоре защемленной балки.
7. Записать систему уравнений равновесия для определения реакций в опорах двухопорной балки, закрепленной на двух шарнирах.
140 Практическое занятие 2
Расчетно-графическая работа 1
Определение реакций в опорах балочных систем под действием сосредоточенных сил и пар сил
Задание 1. Определить величины реакций в опоре защемленной балки. Провести проверку правильности решения.
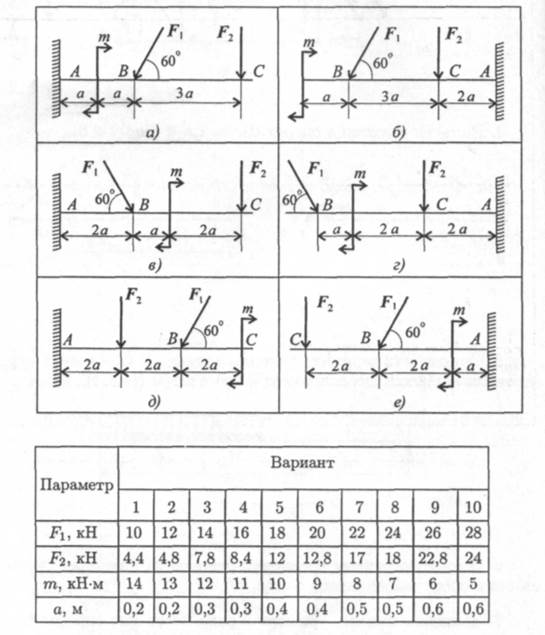
Практическое занятие 2 141
Задание 2. Определить величины реакций для балки с шарнирными опорами. Провести проверку правильности решения.
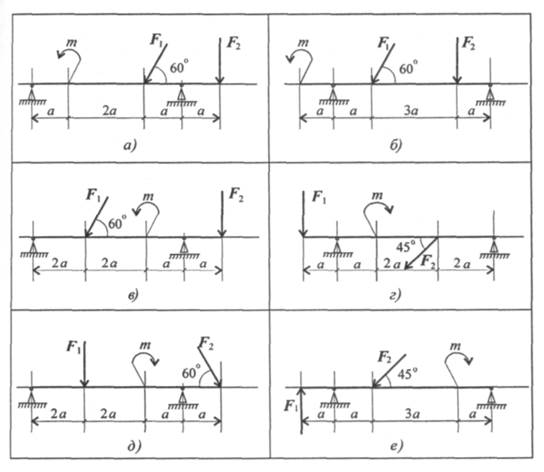
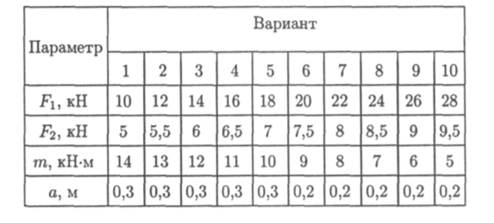
142 Практическое занятие 2
Расчетно-графическая работа 2
Определение величин реакций в опорах балочных систем под действием сосредоточенных и распределенных нагрузок
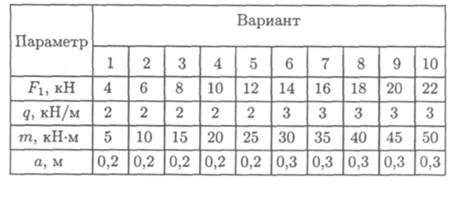
Задание 1. Определить величины реакций в заделке. Провести проверку правильности решения.
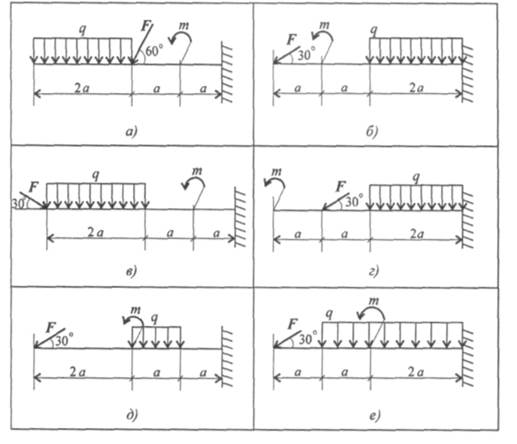
Практическое занятие 2 143
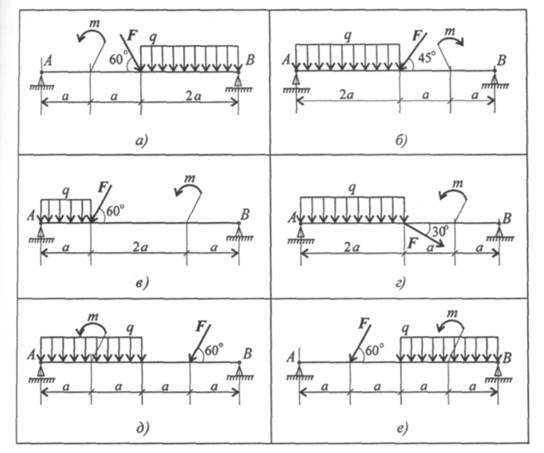
Задание 2. Определить величины реакций в шарнирных опорах балки. Провести проверку правильности решения.
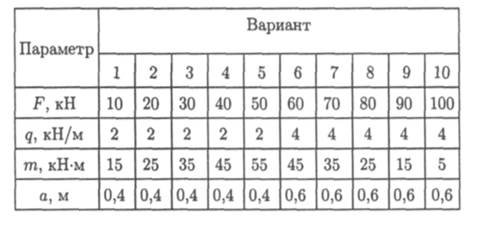
При защите работ ответить на вопросы карт с тестовыми заданиями.
144 Практическое занятие 2
Тема 1.4. Статика.
Произвольная плоская система сил

Практическое занятие 2 145
146 Практическое занятие 3
Практическое занятие 3
Тема 1.6. Центр тяжести
Знать методы определения центра тяжести тела и плоских сечений, формулы для определения положения ЦТ плоских сечений.
Уметь определять положение центра тяжести сложных геометрических фигур, определять положение центра тяжести фигур, составленных из стандартных профилей.
Основные формулы и предпосылки расчета
Центры тяжести простейших сечений (рис. П3.1)
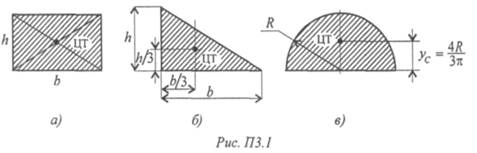
Геометрические характеристики стандартных прокатных профилей в Приложении 2.
Методы расчета:
1) метод симметрии;
2) метод разделения на простые части;
3) метод отрицательных площадей.
Координаты центров тяжести сложных и составных сечений:
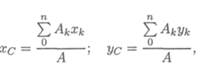
где Ak — площади частей сечения; xk; y k — координаты ЦТ частей cечения; А —
n
суммарная площадь сечения, А = ∑ Ак .
0
Практическое занятие 3 147
Дата добавления: 2019-09-13; просмотров: 2404; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
