Правила принудительного ранжирования
ВВЕДЕНИЕ
Первая стадия – это применение математических методов для анализа и обработки результатов экспериментов и наблюдений и установление простейших количественных закономерностей.
Вторая стадия заключалась в попытке моделирования процессов и явлений с помощью готового математического аппарата, разработанного ранее для других наук.
Третий этап математизации (современный этап) характеризуется разработкой специализированного математического аппарата для исследования и моделирования процессов и явлений.
«математическая статистика» – наука о случайных явлениях, включающая описание случайных явлений, проверку гипотез, изучение причинных зависимостей.
Основными разделами математической статистики считаются разделы описательной статистики, теория статистического вывода, планирование и анализ экспериментов.
Описательная статистикавключает в себя табулирование, представление и описание совокупностей данных. Эти данные могут быть либо количественными, как, например, измерения роста и веса, либо качественными, как, например, пол и тип личности. Описательная статистика упорядочивает и систематизирует имеющуюся информацию, облегчает понимание изучаемого явления.
Наиболее ярким примером статистического описания служат результаты переписи населения, представленные в виде соответствующих таблиц, графиков и показателей распределения населения по демографическим и социальным признакам.
|
|
|
Всякая большая группа испытуемых, относительно которых мы хотим провести исследование и собираемся делать выводы, называется генеральной совокупностью.
Выборка – это часть испытуемых, выделенная из генеральной совокупности для проведения эксперимента.
Теория статистического вывода – это формализованная система методов решения задач, в которой выводятся свойства генеральной совокупности данных путем исследования выборки.
Например, директор крупного концерна хочет определить долю сотрудников, которые положительно относятся к введению нового графика работы. Излишне было бы опрашивать каждого сотрудника, если бы можно было надежно определить такую долю по выборке минимальным объемом, скажем, в 100 человек. Но какова доля тех сотрудников, которые положительно отнеслись в этой выборке из 100 человек, по отношению к доле во всей совокупности сотрудников? Ответ можно получить благодаря теории статистического вывода. Таким образом, задача статистического вывода состоит в том, чтобы предсказать свойства всей совокупности, зная свойства только выборки из этой совокупности. Эти выводы делаются и производятся с помощью методов описательной статистики посредством описания как свойств выборок, так и совокупностей.
|
|
|
Планирование и анализ экспериментовпредставляет собой третью важную ветвь статистических методов, разработанную для обнаружения и проверки причинных связей между переменными.
К особенностям применения математических методов обработки в относятся следующие утверждения:
- чем ближе к реальности экспериментальные данные, тем надежнее результат математического исследования;
- при использовании математических методов для анализа и обработки результатов экспериментов и наблюдений большую часть успеха исследования составляют определение типа решаемой задачи и выбор метода решения;
- важную часть решения задачи занимает интерпретация полученного результата.
РАЗДЕЛ I
 |
ТЕМА 1
 |
ИЗМЕРЕНИЯ
ПРИЗНАКИ И ПЕРЕМЕННЫЕ
Существует множество определений «измерения», несколько отличающихся друг от друга. Общим во всех определениях является следующее: измерение – это приписывание числовых форм объектам или событиям в соответствии с определенными правилами (например, вес, рост, IQ). Измерить рост человека – значит приписать число расстоянию между макушкой человека и подошвой его ног, найденному с помощью линейки. Измерение коэффициента интеллектуальности человека – это присвоение числа характеру ответной реакции, возникающей у него на группу типовых задач.
|
|
|
Измеряемые явления называют признаками (переменными или наблюдениями). Такими явлениями могут быть решения задачи, показатель интеллектуальности, уровень тревожности, количество допущенных ошибок в тесте.
Переменные считаются случайными, т.к. нельзя определить заранее, какое значение они принимают.
Математическая обработка подразумевает оперирование с показателями переменных, полученных в исследованиях.
Показатель (уровень или наблюдаемое значение) – это количественная характеристика измеряемого явления. Значения признака определяются при помощи специальных шкал измерения.
ШКАЛЫ ИЗМЕРЕНИЯ
С. Стивенсом предложена классификация из 4 типов шкал измерения:
1) номинативная, или номинальная, или шкала наименований;
2) порядковая, или ординальная шкала;
3) интервальная, или шкала равных интервалов;
4) шкала равных отношений.
|
|
|
Номинативная шкала – это шкала, классифицирующая по названию: nomen (лат.) – имя, название. Название же не измеряется количественно, оно лишь позволяет один объект отличить от другого. Номинативная шкала – способ классификации объектов и субъектов, распределение их по ячейкам классификации.
Например, классификация объектов по следующим признакам:
§ пол (мужской, женский);
§ цвет глаз (голубой, зеленый и т.д.);
§ клинические диагнозы;
§ автомобильные номера;
§ номера на футболках.
Шкала, состоящая только из двух групп объектов, называется дихотомической, например: «иностранец – соотечественник»; «проголосовал «за» – проголосовал «против»»; «имеет братьев или сестер – единственный ребенок в семье» и т.п.
Единица измерения в номинативной шкале – количество наблюдений или частота, например, в группе 12 женщин и пять мужчин. Точнее, единица измерения – это одно наблюдение. В этой шкале используется лишь отличие классов, но ничего не утверждается относительно того, больше или меньше у объекта А измеряемого свойства в сравнении с объектом В.
Порядковая шкала – это шкала, классифицирующая по принципу «больше – меньше». Если в шкале наименований было безразлично, в каком порядке располагаются классы, то порядковая шкала подразумевает расположение объектов в каком-либо порядке или распределение на классы. К типичным примерам порядковой шкалы можно отнести военные ранги, школьные классы, шкалу человеческих ценностей.
В порядковой шкале должно быть не менее трех классов, например, «подходит для должности – подходит с оговорками – не подходит».
В порядковой шкале не известно истинное расстояние между классами. Чем больше в шкале классов, тем больше возможностей для математической обработки полученных данных и проверки статистических гипотез. Оптимальное количество классов – 12-15.
От классов легко перейти к числам, если условимся считать, что высший класс получает ранг 1, средний – ранг 2, низший – ранг 3, или наоборот. Присвоение каждому классу числового значения – ранга называется ранжированием.
Единица измерения в порядковой шкале – расстояние в 1 класс или 1 ранг, при этом расстояние между классами и рангами может быть разным. Из арифметических операций возможна проверка на соответствие и сравнение.
Интервальная шкала – это шкала, классифицирующая по принципу «больше на определенное количество единиц – меньше на определенное количество единиц». Каждое из возможных значений признака отстоит от другого на равном расстоянии. Например, шкала по Цельсию, шкала по Фаренгейту, исчисление лет по годам, шкалы в единицах стандартного отклонения, процентильные шкалы.
Числа, приписываемые в процессе интервального измерения, имеют свойства однозначности и упорядоченности. Число, присвоенное предмету, представляет собой количество единиц измерения, которое он имеет. Сегодня температура 16° по Цельсию, вчера была 13°. Сегодня на 3° теплее, чем вчера. Если завтра температура будет 22°, то вчера и сегодня имеют больше сходства с точки зрения температуры, чем вчера и завтра.
Основная особенность интервальных шкал, – что свойства предмета не пропадают, если результат измерения равен нулю; например, 0°С не обозначает отсутствие температуры.
Из арифметических операций возможна проверка на соответствие, сравнение и сложение.
Шкала равных отношений – это шкала, классифицирующая объекты и субъекты пропорционально степени выраженности измеряемого свойства. В шкалах отношений классы обозначаются числами, которые пропорциональны друг другу. Главное отличие шкалы равных отношений – наличие абсолютной точки отсчета, т.е. если результат измерения равен нулю, то это говорит об отсутствии измеряемого свойства.
Примером переменных, измеряемых в шкале равных отношений, могут являться абсолютная температура по Кельвину, рост, время, вес.
К переменным в этой шкале применимы все арифметические операции.
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Дайте определения следующим понятиям:
§ измерение, признаки и показатели в психологии;
§ номинативная шкала;
§ дихотомическая шкала;
§ порядковая шкала;
§ шкала отношений;
§ интервальная шкала.
2. Приведите примеры переменных и показателей в психологии.
3. В исследовании фиксировалась скорость решения новой задачи учащимися 1-го класса. Результаты исследования:
§ Верещагина – 4 минуты;
§ Голодов – 2 минуты;
§ Андреева – 3,5 минуты.
Выделите в этой ситуации признак и показатели.
4. Отнесите каждое из следующих измерений к одному из типов шкал:
§ метрическая система измерений расстояний;
§ числа, кодирующие темпераменты;
§ телефонные номера;
§ результаты контрольной работы по чтению (количество прочитанных слов в минуту);
§ числовая ось;
§ умение водить машину;
§ школьные оценки.
5. Перечислите, какие математические операции можно производить с показателями вышеперечисленных шкал.
6. Может ли показатель в какой-нибудь шкале отнести одновременно к двум классам.
7. Группу испытуемых разделили на два класса:
§ стаж работы до 10 лет;
§ стаж работы более 10 лет.
Можно ли отнести это разбиение к порядковой шкале?
8. К какому типу шкал относиться часто используемый в психологии семантический дифференциал Ч. Осгуда для измерения социальных установок, ценностных ориентацией и т.п.:
| -3 | -2 | -1 | 0 | +1 | +2 | +3 | |||||||||||||
|
|
|
|
|
|
| ||||||||||||||
| абсолютно не согласен |
| не знаю |
| абсолютно согласен | |||||||||||||||
ТЕМА 2
| |
ПРЕДСТАВЛЕНИЕ ДАННЫХ
Любой метод исследования, будь то наблюдение, опрос или анализ документов, позволяет получить разнообразную информацию об изучаемом объекте. Обработать и обобщить эту информацию – значит получить новые знания, сделать их доступными для других специалистов, использовать для выработки рекомендаций при принятии решений. С этой целью сведения, полученные в ходе исследования, нужно преобразовать в форму исходных данных для обработки.
Принципы упорядочения, преобразования и отображения эмпирических данных включают: во-первых, подготовку данных к статистической обработке (группировку, табулирование), во-вторых, графическое представление данных (в форме гистограмм, полигона и кумуляты), в-третьих, статистическую обработку данных.
ГРУППИРОВКА ДАННЫХ
Группировка – это объединение вариант в интервалы, границы которых устанавливаются произвольно и непременно указываются. Получаемая в итоге величина называется частотой появления признака. Группировка данных – это суммирование частоты появления признака или некоторых значений признаков в изучаемом массиве объектов по определенным позициям. Математический смысл обработки исходных данных при использовании метода группировки заключается в суммировании данных по частоте появлений некоторых значений.
Наиболее легким из известных методов обработки является метод простой группировки данных. Например, результаты тестирования студентов 1-го курса по философии распределились следующим образом:
1 – ответили на «отлично» – 10 чел.;
2 – ответили на «хорошо» – 34 чел.;
3 – ответили на «удовлетворительно» – 94 чел.;
4 – получили «неудовлетворительно» – 18 чел.;
5 – не участвовали в тестировании – 12 чел.
ТАБУЛИРОВАНИЕ ДАННЫХ
Наиболее распространенной формой группировки экспериментальных данных являются статистические таблицы. Таблицы бывают сложные и простые. К простым относятся таблицы, применяемые при альтернативной группировке, когда одна группа испытуемых противопоставляется другой; например, здоровые – больным, высокие люди – низким и т.п. Пример простой таблицы приведен ниже (см. таблицу 2.1). В ней представляются результаты обследования мануальной асимметрии у 110 учащихся 3-6-х классов.
Таблица 2.1
| Классы | Праворукие | Леворукие | Сумма |
| 3 и 4 | 43 | 6 | 49 |
| 5 и 6 | 44 | 17 | 61 |
| Сумма | 87 | 23 | 110 |
Усложнение таблицы рекомендуется использовать, когда измерение изучаемых признаков производится в номинативной или порядковой шкале.
Усложнение таблицы происходит за счет возрастания объема и степени дифференцированности представленной в них информации. К сложным таблицам относятся так называемые многопольные таблицы, которые могут использоваться при выяснении причинно-следственных отношений между варьирующими признаками. Примером сложной таблицы служит таблица 2.2, в которой представлены классические данные Ф.Гальтона, иллюстрирующие наличие положительной зависимости между ростом родителей и их детей. Таблица организована таким образом, что позволяет оценить частоту встречаемости в популяции однозначно фиксируемых соотношений роста родителей и роста ребенка.
Таблица 2.2
| Рост родителей | Рост детей в дюймах | Всего | |||||||
| 60,7 | 62,7 | 64,7 | 66,7 | 68,7 | 70,7 | 72,7 | 74,7 | ||
| 74 | 4 | 4 | |||||||
| 72 | 1 | 4 | 11 | 17 | 20 | 6 | 62 | ||
| 70 | 1 | 2 | 21 | 48 | 83 | 66 | 22 | 8 | 251 |
| 68 | 1 | 15 | 56 | 130 | 148 | 69 | 11 | 430 | |
| 66 | 1 | 15 | 19 | 56 | 41 | 11 | 1 | 144 | |
| 64 | 2 | 7 | 10 | 14 | 4 | 37 | |||
| Всего | 5 | 39 | 107 | 255 | 387 | 163 | 58 | 14 | 928 |
Правильно составленные таблицы – это большое подспорье в экспериментальной работе, позволяющее одновременно осуществлять разные варианты группировки полученных данных.
РАНГОВЫЙ ПОРЯДОК
Ранжирование – это расположение данных в порядке возрастания или убывания.
Ранжирование может быть простым и принудительным. При простом ранжировании количество рангов меньше количества ранжируемых признаков. Например, если разделить группу людей, претендующих на должность АФК, по признаку соответствия предъявляемым требованиям, ранг 1 получат претенденты, соответствующие предъявляемым требованиям, ранг 2 – претенденты частично соответствующие требованиям, ранг 3 – претенденты, не соответствующие требованиям.
В этих случаях не всегда можно все признаки уместить в несколько рангов. Признаки, имеющие один ранг, могут сильно отличаться.
Принудительное ранжирование используется в случае, когда количество рангов равно количеству признаков.
При принудительном ранжировании разные ранги могут искусственно преувеличивать расстояние между рангами. В разных группах один испытуемый может иметь ранг, отличный от того, какой он имел бы в другой группе.
Правила принудительного ранжирования
1) Наименьшему числовому значению начисляется ранг 1.
2) Наибольшему числовому значению – ранг, равный n – количеству ранжируемых величин.
3) Если несколько числовых значений равны, то им начисляется ранг, равный среднему значению из тех рангов, которые они получили бы, если бы не были равны.
4) Правильность начисления рангов проверяется формулой:
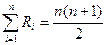, (2.1)
где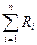 
– сумма всех рангов,
n – количество ранжируемых величин.
5) Не рекомендуется ранжировать более 20 величин, поскольку в этом случае ранжирование в целом окажется малоустойчивым.
6) При необходимости ранжирования достаточно большого числа объектов их следует объединять по какому-либо признаку в достаточно однородные классы, а затем уже ранжировать полученные классы.
Пример начисления рангов для результатов тестирования представлен в таблице 2.3.
Таблица 2.3
| Нумерация результатов (механическое ранжирование) | Фамилия | Результат | Ранг |
| 1 | Сорокин А. | 71 | 1 |
| 2 | Андрейченко Н. | 73 | 2 |
| 3 | Алексеев Л. | 75 | 4 |
| 4 | Иванов В. | 75 | 4 |
| 5 | Ростова А. | 75 | 4 |
| 6 | Липова О. | 84 | 6 |
| 7 | Кочеткова А. | 87 | 7 |
| 8 | Васильев Н. | 88 | 8,5 |
| 9 | Шепетов А. | 88 | 8,5 |
| 10 | Гроз И. | 90 | 10 |
| Сумма | 55 |
В примере встречаются три значения 75, в обычной нумерации они получили бы ранг 3, 4, 5. Таким образом, каждое из них получает ранг, равный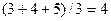 
.
Для проверки правильности начисления рангов найдем:
, 
.
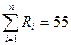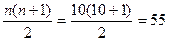РАСПРЕДЕЛЕНИЕ ЧАСТОТ
При описании общей картины результатов теста список студентов из таблицы можно сократить, классифицируя баллы по распределению частот, иногда называемому распределением.
Числа, показывающие, сколько раз варианты встречаются в данной совокупности, называются частотами, или весами вариант. Они обозначаются fi и имеют индекс « i», соответствующий номеру переменной.
Частость (относительная частота) – доля каждой частоты fi в общем объеме выборки n:
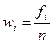. (2.2)
В таблице 2.4 приведен пример нахождения частоты и частости результатов тестирования из таблицы 2.3.
В случае большого диапазона разброса данных имеет смысл обобщение данных в виде группирования по интервалам. Правила выбора количества интервалов не существует, но предпочтительно группировать по 12-15 интервалам (классам).
Ширина интервалов (класса) должна быть одинаковой и равной
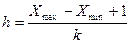, (2.3)
где h – ширина интервалов;
k – количество классов;
Xmax – максимальное значение из данных;
Xmin – минимальное значение из данных.
Таблица 2.4
| Баллы Х i | Частота fi | Частость wi |
| 71 | 1 | 0,1 |
| 73 | 1 | 0,1 |
| 75 | 3 | 0,3 |
| 84 | 1 | 0,1 |
| 87 | 1 | 0,1 |
| 88 | 2 | 0,2 |
| 90 | 1 | 0,1 |
| Сумма | 10 | 1,0 |
Количество классов выбирается таким образом, чтобы ширина была целым числом.
Задача 2.1
Данные из таблицы 2.4 необходимо разбить на интервалы, найти середины интервалов, а также частоту и частость в интервалах.
Максимальный балл равен 90 баллам, минимальный – 71. Ширина определяется по формуле (2.3):
.
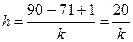Для того чтобы ширина была целым числом, количество интервалов должно быть или 4, или 5, или 10.
Найдем ширину интервалов при количестве интервалов, равном пяти:
.
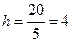Определение середины интервала состоит в усреднении зафиксированных границ интервала. Например, для первого интервала середина будет (74+71)/2=72,5. Занесем все вычисления в таблицу 2.5.
Таблица 2.5
| Интервал | Середина интервала | Частота | Относительная частота |
| 71-74 | 72,5 | 2 | 0,2 |
| 75-78 | 76,5 | 3 | 0,3 |
| 79-82 | 80,5 | ||
| 83-86 | 84,5 | 1 | 0,1 |
| 87-90 | 88,5 | 4 | 0,4 |
| Сумма | 10 | 1,0 |
СТАТИСТИЧЕСКИЕ РЯДЫ
Особую форму группировки данных представляют так называемые статистические ряды, или числовые значения признака, расположенного в определенном порядке.
В зависимости от того, какие признаки изучаются, статистические ряды делят на атрибутивные, вариационные, ряды динамики, регрессии, ряды ранжированных значений признаков и ряды накопленных частот. Наиболее часто в психологии используются вариационные ряды, ряды регрессии и ряды ранжированных значений признаков.
Вариационным рядом распределения называют двойной ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью в данной выборке. Например, результаты вступительного тестирования оказались следующими: 71, 75, 84, 75, 87, 84, 75, 88, 90, 88. Как видим, некоторые цифры попадаются в данном ряду по несколько раз. Следовательно, учитывая число повторений, данные ряда можно представить в более удобной, компактной форме:
| Варианты | xi | 73 | 71 | 75 | 87 | 84 | 88 | 90 | (2.4) |
| Частоты вариант | fi | 1 | 1 | 3 | 1 | 1 | 2 | 1 |
Это и есть вариационный ряд. Числа, показывающие, сколько раз отдельные варианты встречаются в данной совокупности, называются частотами, или весами, вариант. Они обозначаются строчной буквой латинского алфавита и имеют индекс «i», соответствующий номеру переменной в вариационном ряду.
Общая сумма частот вариационного ряда равна объему выборки, т.е.
.
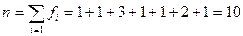Частоты можно выражать и в процентах. При этом общая сумма частот или объем выборки принимается за 100%. Процент каждой отдельной частоты или веса подсчитывается по формуле:
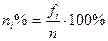. (2.5)
Процентное представление частот полезно в тех случаях, когда приходится сравнивать вариационные ряды, сильно различающиеся по объемам. Например, при тестировании школьной готовности детей города, поселка городского типа и села были обследованы выборки детей численностью 1000, 300 и 100 человек соответственно. Различие в объемах выборок очевидно. Поэтому сравнение результатов тестирования лучше проводить, используя проценты частот.
Приведенный выше ряд (2.4) можно представить по-другому. Если элементы ряда расположить в возрастающем порядке, то получится так называемый ранжированный вариационный ряд:
| Варианты | xi | 71 | 73 | 75 | 84 | 87 | 88 | 90 | (2.6) |
| Частоты вариант | fi | 1 | 1 | 3 | 1 | 1 | 2 | 1 |
Подобная форма представления (2.6) более предпочтительна, чем (2.4), поскольку лучше иллюстрирует закономерность варьирования признака.
Частоты, характеризующие ранжированный вариационный ряд, можно складывать или накапливать. Накопленные частоты получаются последовательным суммированием значений частот от первой частоты до последней.
В качестве примера вновь обратимся к ряду 2.6. Преобразуем его в ряд 2.7, в котором введем дополнительную строчку и назовем ее «кумуляты частот».
| Варианты | xi | 71 | 73 | 75 | 84 | 87 | 88 | 90 | |
| Частоты вариант | fi | 1 | 1 | 3 | 1 | 1 | 2 | 1 | (2.7) |
| Кумуляты частот | 1 | 2 | 5 | 6 | 7 | 9 | 10 |
ПОНЯТИЕ РАСПРЕДЕЛЕНИЯ
И ГИСТОГРАММЫ
В статистике под рядом распределенияпонимают распределение частот по вариантам. Измеренные величины признака в выборке варьируют в пределах от минимального до максимального значения. Этот предел разбивают на так называемые классовые интервалы, которые, в зависимости от конкретных данных, могут быть как равными по величине, так и неравными.
Существует четыре общих метода графического представления распределения частот: гистограмма, полигон распределения и сглаженная кривая, кумулятивный полигон.
Если по оси абсцисс – OX откладывать величины классовых интервалов, а по оси ординат – OY – величины частот, попадающих в данный классовый интервал, то получается так называемая гистограмма распределения частот. При этом над каждым классовым интервалом строится колонка или прямоугольник, площадь которого оказывается пропорциональной соответствующей частоте. Пример построения гистограммы представлен на рисунке 2.1.
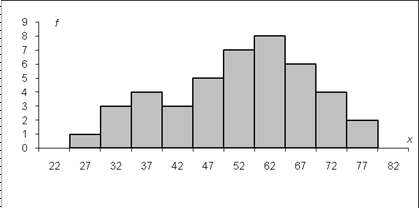
Рис.2.1. Гистограмма результатов тестирования 43 абитуриентов.
Гистограмма представляет собой графическое изображение данного частотного распределения. Виды распределения представлены на рисунке 2.2.
Построение полигона распределения во многом напоминает построение гистограммы. В гистограмме каждый столбец заканчивается горизонтальной линией, причем на высоте, соответствующей частоте в этом разряде. А в полигоне он заканчивается точкой над серединой своего разрядного интервала на той же высоте. Далее точки соединяются отрезками прямых (см. рисунок 2.3). – это и будет полигон распределения.
Если эти же точки соединить плавной линией – получим сглаженную кривую распределения (см. рисунок 2.4).
Если по оси OY откладывать кумуляты частот, то получим кумулятивный полигон (см. рисунок 2.5).
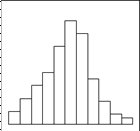
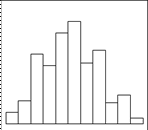
а) Обычный тип б) Гребенка
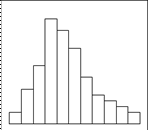
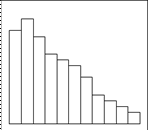
в) Положительно г) Распределение с
скошенное распределение обрывом слева
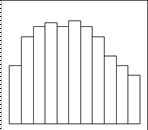
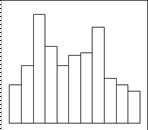
д) Плато е) Двухпиковый тип
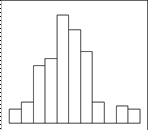
ж) Распределение с изолированным пиком
Рис. 2.2. Виды гистограмм.
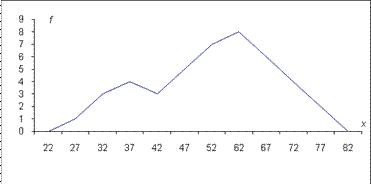
Рис.2.3. Полигон распределения,
представляющий результаты тестирования 43 абитуриентов.
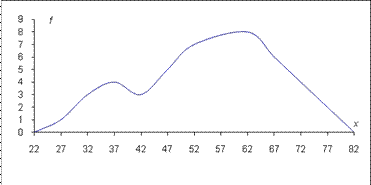
Рис.2.4. Кривая распределения результатов тестирования 43 абитуриентов.
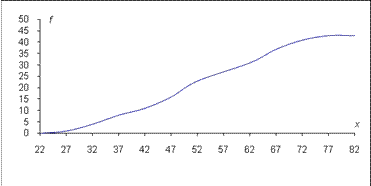
Рис.2.5. Кумулятивный полигон.
? ВОПРОСЫ И УПРАЖНЕНИЯ
1. Дайте определение следующим понятиям: группировка данных, ранжирование, ранг, частота, частость, статистический и вариационный ряды, распределение, гистограмма, полигон распределения и сглаженная кривая.
2. В исследовании
3. Эта задача – на построение группового распределения частот. Следующие данные представляют собой оценки 75 взрослых людей в тесте на определение коэффициента интеллектуальности Стенфорда-Бине:
| 141 | 104 | 101 | 130 | 148 |
| 92 | 87 | 115 | 96 | 91 |
| 100 | 133 | 124 | 123 | 92 |
| 132 | 118 | 98 | 107 | 101 |
| 97 | 124 | 118 | 107 | 146 |
| 110 | 111 | 138 | 129 | 121 |
| 106 | 135 | 97 | 108 | 108 |
| 107 | 110 | 101 | 105 | 129 |
| 105 | 110 | 116 | 123 | 113 |
| 83 | 127 | 112 | 105 | 114 |
| 127 | 114 | 113 | 139 | 106 |
| 95 | 105 | 95 | 106 | 105 |
В задаче:
· сгруппируйте результаты наблюдений;
· определите частоту и частость показателей;
· выберите интервал группирования разрядов;
· постройте распределение сгруппированных частот, полигон распределения и сглаженную кривую.
- Проведите ранжирование следующих результатов наблюдений: 10, 12, 11, 13, 12, 7, 8, 6, 11, 8, 12, 14, 11.
 |
ТЕМА 3
| |
МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ
Свойства совокупности данных можно представить в форме графиков или таблиц. Часто график или таблица говорят больше, чем мы хотим или должны знать, а передаваемая информация может оцениваться временем, потребным на сообщение. Поэтому обычно используется для описания совокупности данных только два-три свойства. Эти свойства (например, «значение», наиболее часто встречающееся среди результатов, или разброс значений) могут быть описаны показателями, известными как «статистики свертки», «методы оценки средних величин» или «меры центральной тенденции».
Термин «статистики» совокупности данных используется при описании выборочной совокупности данных. Если речь идет о генеральной совокупности, то ее показатели именуются «параметрами».
МОДА
Наиболее просто получаемой мерой центральной тенденции является мода. Мода – это значение во множестве наблюдений, которое встречается наиболее часто.
В совокупности значений (1, 2, 2, 7, 8, 8, 8, 10) модой является 8, потому что оно встречается чаще любого другого значения. Мода представляет собой наиболее частое значение (в данном примере 8), а не частоту этого значения (в примере равную 3).
Однако не всякая совокупность значений имеет единственную моду в строгом понимании этого определения, поэтому рабочее определение моды содержит особенности и соглашения.
1. В случае, когда все значения в группе встречаются одинаково часто, принято считать, что группа оценок не имеет моды. Так, в группе (0,2; 0,2; 2,3; 2,3; 4,1; 4,1) моды нет.
2. Когда два соседних значения имеют одинаковую частоту и они больше частоты любого другого значения, мода есть среднее этих двух значений. Итак, мода группы значений (0,1, 1, 2, 2, 2, 3, 3, 3, 4) равна 2,5.
3. Если два несмежных значения в группе имеют равные частоты и они больше частот любого значения, то существуют две моды. В группе значений (5, 7, 7, 7, 10, 11, 12, 12, 12, 17) модами являются и 7 и 12. В таком случае говорят, что группа оценок является бимодальной.
Замечание
Большие множества данных часто рассматриваются как бимодальные, когда они образуют полигон частот, похожий на спину бактриана – верблюда двугорбого, даже если частоты на двух вершинах не строго равны. Это незначительное искажение определения вполне оправданно, ибо термин «бимодальный» допустим и удобен для описания. Можно условиться различать большие и меньшие моды.
Наибольшей модой в группе называется единственное значение, которое удовлетворяет определению моды. Однако во всей группе может быть и несколько меньших мод. Эти меньшие моды представляют собой, в сущности, локальные вершины распределения частот.
Например, на рисунке 3.1 наибольшая мода наблюдается при значении 6, а меньшие – при 3,5 и 10.
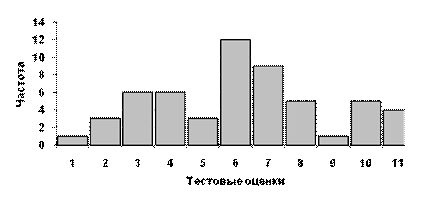
Рис. 3.1. Распределение частот тестовых оценок с наибольшей модой 6 и меньшими модами 3,5 и 10.
МЕДИАНА
Медиана (Md) – значение, которое делит упорядоченное множество данных пополам, так что одна половина значений оказывается больше медианы, а другая – меньше.
Вычисление медианы
1. Если данные содержат нечетное число различных значений, то медиана есть среднее значение для случая, когда они упорядочены. Например, в группе (17, 19, 21, 24, 27) медиана равна 21.
2. Если данные содержат четное число различных значений, то медиана есть точка, лежащая посредине между двумя центральными значениями, когда они упорядочены. В группе (3, 11, 16, 20) медиана вычисляется как (11+ 16)/2 = 13,5.
3. Если в данных есть объединенные классы, особенно в окрестности медианы, возможно, потребуется табулирование частот.
В таких случаях придется интерполировать внутри разряда значений.
Задача 3.1
Пусть, например, 36 значений, упорядоченных от 7,0 до 10,5, имеют следующее распределение:
| Значение | Частота | Накопленная частота |
| 10,5 | 2 | 36 |
| 10,0 | 3 | 34 |
| 9,5 | 2 | 31 |
| 9,0 | 6 | 29 |
| 8,5 | 10=5+5 | 23 |
 8,0
| 8 | 13 |
| 7,5 | 4 13 | 5 |
| 7,0 | 1 | 1 |
| n=36 |
Оценкой медианы будет величина n/2, равная 18-му значению снизу. Медиана будет находиться по формуле:
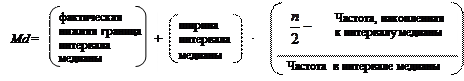
(3.1)
В задаче 3.1:
§ фактическая нижняя граница интервала равна 8,25;
§ ширина интервала медианы равна 0,5;
§ оценка медианы n/2 = 36/2 =18;
§ частота, накопленная к интервалу медианы, равна13;
§ частота в интервале медианы равна 10.
Подставляя найденные значения в формулу (3.1), получим:
Md = 8,25 + 0,5× (18-13) /10 = 8,5.
СРЕДНЕЕ
Третья мера – среднее выборочное, называемое иногда «средним», «арифметическим средним» или «математическим ожиданием».
Среднее выборочной совокупности п значений определяется как
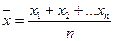
или:
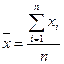. (3.2)
Если даны значения и частоты их повторения, то среднее значение определяется формулой:
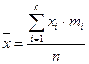. (3.3)
Найдем, например, среднее для значений из задачи 3.1:
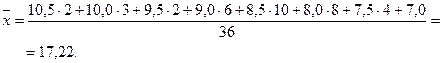
Если даны значения в интервале, тогда за xi берутся середины интервалов.
Соответствующим параметром генеральной совокупности будет средняя генеральной совокупности m, которая вычисляется по формуле (3.4), аналогичной формуле (3.2):
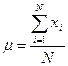, (3.4)
где N – численность или объем генеральной совокупности.
Свойства среднего
1) Сумма всех отклонений от среднего значения равна нулю:
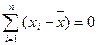. (3.5)
2) Если константу прибавить к каждому значению, то среднее увеличится ровно на эту константу:
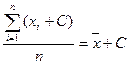. (3.6)
3) Если каждое значение умножить на константу с, то среднее увеличится в с раз:
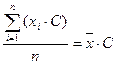. (3.7)
4) Сумма квадратов отношений значений от их среднего значения меньше суммы квадратов отклонений от любой другой точки:
. (3.8)
Дата добавления: 2019-09-13; просмотров: 490; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!