Закон Кулона – основной закон электростатики

Сила электрического взаимодействия двух покоящихся точечных зарядов в вакууме прямо пропорциональна произведению модулей этих зарядов и обратно пропорциональна квадрату расстояния между ними. Это сила притяжения, если заряды разноимённые, и отталкивания, если они одноимённые. Сила направлена вдоль прямой, проходящей через точечные заряды.

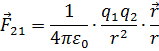
Здесь 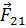 - сила, действующая на второй заряд со стороны первого,  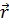– радиус-вектор, проведенный от первого заряда ко второму. По третьему закону Ньютона на первый заряд со стороны второго действует равная и противоположно направленная сила 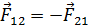. Коэффициент пропорциональности имеет вид  – электрическая постоянная системы СИ.

(Опр.) Напряжённостью электрического поля называется отношение силы, действующей на пробный (точечный) заряд, помещённый в данную точку поля, к величине этого пробного заряда q_пр:

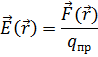
Выражение для напряжённости электрического поля, создаваемого в окружающем пространстве одиночным точечным зарядом, легко получить, исходя из определения напряжённости и из закона Кулона:

 

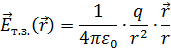
Принцип суперпозиции

Каждое электрическое воздействие на точечный заряд q_пр (назовём его пробным) со стороны каждого отдельного из группы зарядов q₁, q₂, …, q_i, …, q_n ≡ {q_i} описывается силой F ̄ _i – векторной величиной, которую можно найти по закону Кулона. Электрическое воздействие со стороны всей группы n зарядов даёт результирующая сила, равная векторной сумме всех сил F ̄ _i:

Так как 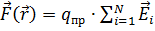 и , получим как следствие принцип суперпозиции для напряжённости электрического поля: .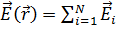

(Опр.) Линии, касательные к которым в каждой точке поля совпадают с направлением вектора напряжённости в данной точке, называются линиями напряжённости электрического поля.

Они помогают представить структуру электрического поля – его направление и величину в разных точках пространства. О величине судят при этом по «густоте» линий напряжённости в данной области пространства, т. е. по их количеству, отнесённому к площади «пронзаемой» поверхности.

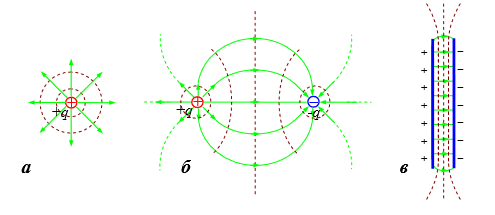На рисунке приведены картины силовых линий поля одиночного точечного заряда – a (для положительного они направлены радиально от заряда); системы из двух разноимённых, одинаковых по модулю зарядов – б; поля между двумя плоскопараллельными разноимённо заряженными пластинами – в.

(Опр.) Разностью потенциалов между точками электростатического поля 1 и 2 называется отношение работы поля по перемещению пробного заряда из точки 1 в точку 2 к величине этого заряда:

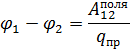
(Опр.) Для энергетической характеристики поля – потенциала – полезно также ввести систему «эквипотенциальных поверхностей». Это поверхности постоянного потенциала, которые характеризуют способность сил поля совершать работу при перемещении заряда.

Вдоль таких поверхностей работа, очевидно, вообще не совершается. Она максимальна по направлениям, по которым максимальна густота (плотность) расположения эквипотенциальных поверхностей. В этих местах максимальна и напряжённость поля. Нетрудно сообразить, какова и взаимная ориентация силовых линий и эквипотенциальных поверхностей в местах их пересечений: они взаимно перпендикулярны.

 

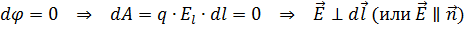
2. Теорема Гаусса. Применение теоремы при расчёте электроёмкости цилиндрического конденсатора.

(Опр.) Элементарным потоком dФ вектора E ̄ через элемент поверхности dS ̄ называется величина:

,

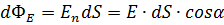где E_n – проекция вектора E ̄ на положительную нормаль n ̄ к элементу поверхности dS ̄.

Полный поток для поля всех заряженных частиц можно вычислить так:

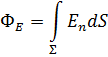
Теорема Гаусса

Поток вектора напряжённости электростатического поля Ф_Е в вакууме через любую замкнутую поверхность ∑ пропорционален суммарному заряду, расположенному внутри этой поверхности.

Коэффициент пропорциональности в системе СИ равен :

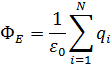
С учётом определения потока вектора напряжённости:

Здесь N – число частиц или тел с зарядами q_i в области пространства Ω, охваченной замкнутой поверхностью ∑. Замкнутая поверхность всегда ограничивает конечную область пространства!

Доказательство.

а) Сферическая поверхность охватывает точечный положительный заряд, расположенный в её центре.

В любой точке пространства вектор напряжённости имеет радиальное направление, а его величина обратно пропорциональна квадрату расстояния от точечного заряда источника поля. Для любого малого элемента сферической поверхности направления векторов E ̄ и dS ̄ совпадают.

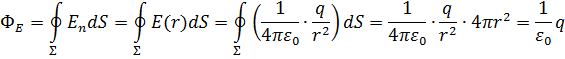
б) Cместим точечный заряд из центра всё той же сферической поверхности.

Для каждого малого элемента поверхности угол между векторами E ̄ и dS ̄ разный, также как разные значения принимает и модуль напряжённости. Вспомним, что поток через поверхность пропорционален числу силовых линий пересекающих эту поверхность. Это число не изменилось при смещении заряда из центра. Поэтому можно предполагать, что остаётся в силе и утверждение теоремы Гаусса.

Отношение 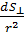 является мерой телесного угла dΩ.

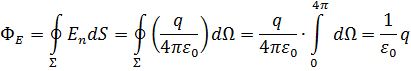
в) Замкнутая поверхность произвольной формы охватывает один точечный заряд.

Число силовых линий, пересекающих поверхность ∑, не изменяется даже в случае самых причудливых замкнутых поверхностей, охватывающих заряд q.

г) Один точечный заряд находится вне замкнутой поверхности произвольной формы.

Для каждой силовой линии число её пересечений с замкнутой поверхностью ∑ число пересечений «внутрь» всегда равно числу «выходов наружу». Поэтому точечный заряд не создаёт дополнительного потока через эту поверхность.

д) Система N точечных зарядов q₁, q₂, ..., q_i, ..., q_N находящихся как внутри, так и вне замкнутой поверхности ∑ произвольной формы.

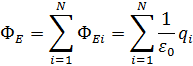
(Опр.) Конденсатором называется система, состоящая из двух проводников, между которыми возникает изолированное от внешних тел электрическое поле при сообщении проводникам равных по модулю и противоположных по знаку зарядов.

(Опр.) Электроёмкостью конденсатора называется отношение модуля заряда каждой из его обкладок к разности потенциалов между ними

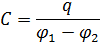
Пример. Расчёт электроёмкости цилиндрического конденсатора.

1. Цилиндрический конденсатор состоит из двух цилиндрических обкладок, разделённых тонким диэлектрическим зазором. Скажем, что на внутреннем электроде радиусом R₁ заряд + q, на внешнем электроде радиусом R₂ заряд - q.

Выберем замкнутую поверхность ∑ радиусом R, R₁ < R < R₂. Поток вектора напряжённости прямого кругового цилиндра равен: 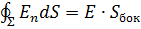. В соответствии с теоремой Гаусса:

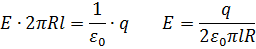
2. Разность потенциалов:

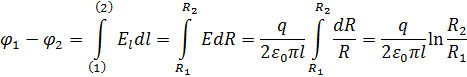
3. Электроёмкость «воздушного» плоского конденсатора (l – длина цилиндра):

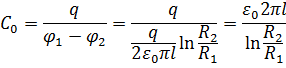
Электроёмкость конденсатора, заполненного однородным диэлектриком:

 

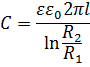
3. Теорема Гаусса. Пример расчёта электроёмкости плоского конденсатора.

(Опр.) Элементарным потоком dФ вектора E ̄ через элемент поверхности dS ̄ называется величина:

,

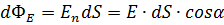где E_n – проекция вектора E ̄ на положительную нормаль n ̄ к элементу поверхности dS ̄.

Полный поток для поля всех заряженных частиц можно вычислить так:

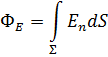
Теорема Гаусса

Поток вектора напряжённости электростатического поля Ф_Е в вакууме через любую замкнутую поверхность ∑ пропорционален суммарному заряду, расположенному внутри этой поверхности.

Коэффициент пропорциональности в системе СИ равен :

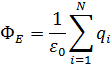
С учётом определения потока вектора напряжённости:

Здесь N – число частиц или тел с зарядами q_i в области пространства Ω, охваченной замкнутой поверхностью ∑. Замкнутая поверхность всегда ограничивает конечную область пространства!

Доказательство.

а) Сферическая поверхность охватывает точечный положительный заряд, расположенный в её центре.

В любой точке пространства вектор напряжённости имеет радиальное направление, а его величина обратно пропорциональна квадрату расстояния от точечного заряда источника поля. Для любого малого элемента сферической поверхности направления векторов E ̄ и dS ̄ совпадают.

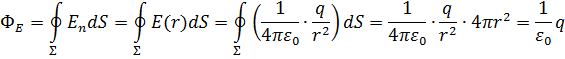
б) Cместим точечный заряд из центра всё той же сферической поверхности.

Для каждого малого элемента поверхности угол между векторами E ̄ и dS ̄ разный, также как разные значения принимает и модуль напряжённости. Вспомним, что поток через поверхность пропорционален числу силовых линий пересекающих эту поверхность. Это число не изменилось при смещении заряда из центра. Поэтому можно предполагать, что остаётся в силе и утверждение теоремы Гаусса.

Отношение 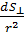 является мерой телесного угла dΩ.

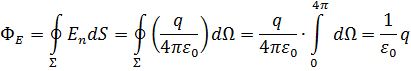
в) Замкнутая поверхность произвольной формы охватывает один точечный заряд.

Число силовых линий, пересекающих поверхность ∑, не изменяется даже в случае самых причудливых замкнутых поверхностей, охватывающих заряд q.

г) Один точечный заряд находится вне замкнутой поверхности произвольной формы.

Для каждой силовой линии число её пересечений с замкнутой поверхностью ∑ число пересечений «внутрь» всегда равно числу «выходов наружу». Поэтому точечный заряд не создаёт дополнительного потока через эту поверхность.

д) Система N точечных зарядов q₁, q₂, ..., q_i, ..., q_N находящихся как внутри, так и вне замкнутой поверхности ∑ произвольной формы.

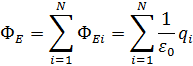
(Опр.) Конденсатором называется система, состоящая из двух проводников, между которыми возникает изолированное от внешних тел электрическое поле при сообщении проводникам равных по модулю и противоположных по знаку зарядов.

(Опр.) Электроёмкостью конденсатора называется отношение модуля заряда каждой из его обкладок к разности потенциалов между ними

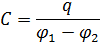
Пример. Расчёт электроёмкости плоского конденсатора.

1. Плоский конденсатор состоит из двух плоскопараллельных проводящих пластин, разделённых тонким диэлектрическим зазором. Рассмотрим одну из пластин, которую будем считать «бесконечной плоскостью»

Поток вектора напряжённости через выбранную нами замкнутую поверхность ∑ прямого кругового цилиндра равен: 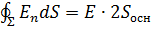. Заряд внутри поверхности равен 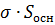, поверхностная плотность заряда 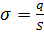. В соответствии с теоремой Гаусса:

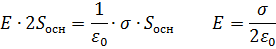
В случае плоского конденсатора силовые линии между пластинами напряжённости полей совпадают по направлению, а вне этой области направлены в противоположные стороны. Следовательно:

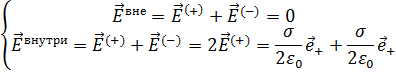
2. Траектория вдоль силовой линии по оси ОХ, от положительной обкладки до отрицательной.

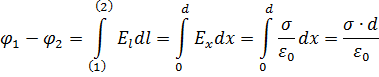
3. Электроёмкость «воздушного» плоского конденсатора (S – площадь обкладок конденсатора, d – расстояние между ними):

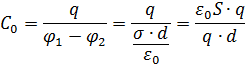
Электроёмкость конденсатора, заполненного однородным диэлектриком:

 

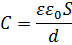
4. Теорема Гаусса. Пример применения теоремы – расчёт электроёмкости сферического конденсатора.

(Опр.) Элементарным потоком dФ вектора E ̄ через элемент поверхности dS ̄ называется величина:

,

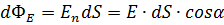где E_n – проекция вектора E ̄ на положительную нормаль n ̄ к элементу поверхности dS ̄.

Полный поток для поля всех заряженных частиц можно вычислить так:

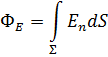
Теорема Гаусса

Поток вектора напряжённости электростатического поля Ф_Е в вакууме через любую замкнутую поверхность ∑ пропорционален суммарному заряду, расположенному внутри этой поверхности.

Коэффициент пропорциональности в системе СИ равен :

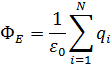
С учётом определения потока вектора напряжённости:

Здесь N – число частиц или тел с зарядами q_i в области пространства Ω, охваченной замкнутой поверхностью ∑. Замкнутая поверхность всегда ограничивает конечную область пространства!

Доказательство.

а) Сферическая поверхность охватывает точечный положительный заряд, расположенный в её центре.

В любой точке пространства вектор напряжённости имеет радиальное направление, а его величина обратно пропорциональна квадрату расстояния от точечного заряда источника поля. Для любого малого элемента сферической поверхности направления векторов E ̄ и dS ̄ совпадают.

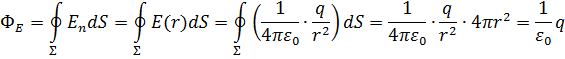
б) Cместим точечный заряд из центра всё той же сферической поверхности.

Для каждого малого элемента поверхности угол между векторами E ̄ и dS ̄ разный, также как разные значения принимает и модуль напряжённости. Вспомним, что поток через поверхность пропорционален числу силовых линий пересекающих эту поверхность. Это число не изменилось при смещении заряда из центра. Поэтому можно предполагать, что остаётся в силе и утверждение теоремы Гаусса.

Отношение 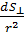 является мерой телесного угла dΩ.

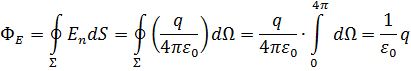
в) Замкнутая поверхность произвольной формы охватывает один точечный заряд.

Число силовых линий, пересекающих поверхность ∑, не изменяется даже в случае самых причудливых замкнутых поверхностей, охватывающих заряд q.

г) Один точечный заряд находится вне замкнутой поверхности произвольной формы.

Для каждой силовой линии число её пересечений с замкнутой поверхностью ∑ число пересечений «внутрь» всегда равно числу «выходов наружу». Поэтому точечный заряд не создаёт дополнительного потока через эту поверхность.

д) Система N точечных зарядов q₁, q₂, ..., q_i, ..., q_N находящихся как внутри, так и вне замкнутой поверхности ∑ произвольной формы.

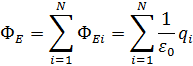
(Опр.) Конденсатором называется система, состоящая из двух проводников, между которыми возникает изолированное от внешних тел электрическое поле при сообщении проводникам равных по модулю и противоположных по знаку зарядов.

(Опр.) Электроёмкостью конденсатора называется отношение модуля заряда каждой из его обкладок к разности потенциалов между ними

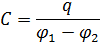
Пример. Расчёт электроёмкости сферического конденсатора.

1. Сферический конденсатор состоит из двух сферических обкладок, разделённых тонким диэлектрическим зазором. Скажем, что на внутреннем электроде радиусом R₁ заряд + q, на внешнем электроде радиусом R₂ заряд - q.

Выберем замкнутую поверхность ∑ радиусом R, R₁ < R < R₂. Поток вектора напряжённости сферы равен: 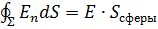. В соответствии с теоремой Гаусса:

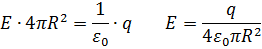
2. Разность потенциалов:

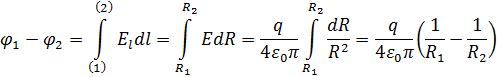
3. Электроёмкость «воздушного» плоского конденсатора:

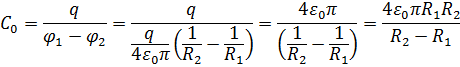
Электроёмкость конденсатора, заполненного однородным диэлектриком:

 

 

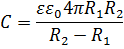
5. Теорема Гаусса. Пример применения – расчёт напряжённости и потенциала электрического поля плоского заряженного слоя.

(Опр.) Элементарным потоком dФ вектора E ̄ через элемент поверхности dS ̄ называется величина:

,

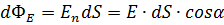где E_n – проекция вектора E ̄ на положительную нормаль n ̄ к элементу поверхности dS ̄.

Полный поток для поля всех заряженных частиц можно вычислить так:

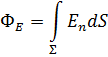
Теорема Гаусса

Поток вектора напряжённости электростатического поля Ф_Е в вакууме через любую замкнутую поверхность ∑ пропорционален суммарному заряду, расположенному внутри этой поверхности.

Коэффициент пропорциональности в системе СИ равен :

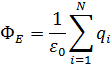
С учётом определения потока вектора напряжённости:

Здесь N – число частиц или тел с зарядами q_i в области пространства Ω, охваченной замкнутой поверхностью ∑. Замкнутая поверхность всегда ограничивает конечную область пространства!

Доказательство.

а) Сферическая поверхность охватывает точечный положительный заряд, расположенный в её центре.

В любой точке пространства вектор напряжённости имеет радиальное направление, а его величина обратно пропорциональна квадрату расстояния от точечного заряда источника поля. Для любого малого элемента сферической поверхности направления векторов E ̄ и dS ̄ совпадают.

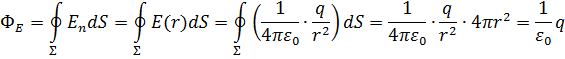
б) Cместим точечный заряд из центра всё той же сферической поверхности.

Для каждого малого элемента поверхности угол между векторами E ̄ и dS ̄ разный, также как разные значения принимает и модуль напряжённости. Вспомним, что поток через поверхность пропорционален числу силовых линий пересекающих эту поверхность. Это число не изменилось при смещении заряда из центра. Поэтому можно предполагать, что остаётся в силе и утверждение теоремы Гаусса.

Отношение 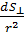 является мерой телесного угла dΩ.

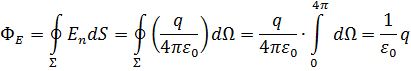
в) Замкнутая поверхность произвольной формы охватывает один точечный заряд.

Число силовых линий, пересекающих поверхность ∑, не изменяется даже в случае самых причудливых замкнутых поверхностей, охватывающих заряд q.

г) Один точечный заряд находится вне замкнутой поверхности произвольной формы.

Для каждой силовой линии число её пересечений с замкнутой поверхностью ∑ число пересечений «внутрь» всегда равно числу «выходов наружу». Поэтому точечный заряд не создаёт дополнительного потока через эту поверхность.

д) Система N точечных зарядов q₁, q₂, ..., q_i, ..., q_N находящихся как внутри, так и вне замкнутой поверхности ∑ произвольной формы.

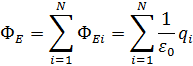
Пример. Расчёт напряжённости и потенциала электрического поля плоского заряженного слоя.

1. Рассмотрим плоский заряженный слой, которую будем считать «бесконечной плоскостью». Поток вектора напряжённости через выбранную нами замкнутую поверхность ∑ прямого кругового цилиндра равен: 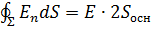. Заряд внутри поверхности равен 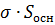, поверхностная плотность заряда 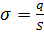. В соответствии с теоремой Гаусса:

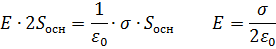
2. Траектория вдоль силовой линии по оси ОХ. Будем считать потенциал равным нулю там, где поле практически отсутствует. S – площадь слоя.

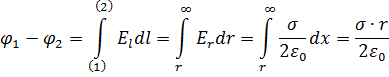
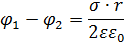
При наличии газообразной или жидкой однородной диэлектрической среды

6. Поле заряженного проводника. Связь поверхностной плотности заряда и напряжённости электрического поля у поверхности проводника.

1. Напряжённость электрического поля в проводниках равна нулю.

2. Потенциал всех точек проводящего тела одинаков.

Т.е. в условиях электростатики проводник является эквипотенциальным телом (φ = const, т.к. E ̄ = - grad φ , а E ̄ = 0).

3. Весь избыточный заряд проводника распределён по его поверхности.

Полный заряд любой макроскопической области внутри проводника равен нулю. Обоснуем, используя теорему Гаусса. Выберем замкнутую поверхность ∑ в виде поверхности, охватывающей всю внутреннюю область проводника за исключением тонкого приповерхностного слоя. Поскольку в любой точке внутри проводника E ̄ = 0, поток вектора напряжённости через выбранную поверхность также равен нулю: 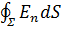. Согласно теореме Гаусса, поток пропорционален заряду внутри поверхности. Следовательно, полный заряд равен нулю, то есть внутри проводника разноимённые заряды скомпенсированы.

4. Вне проводника силовые линии электростатического поля вблизи от его поверхности перпендикулярны к ней.

Линии напряжённости всегда перпендикулярны эквипотенциальным поверхностям, которые они пересекают или подходят к ним, какой является поверхность проводника.

5. Напряжённость поля заряженного проводника вблизи поверхности пропорциональна поверхностной плотности заряда.

Напряжённость поля заряженного проводника вблизи его поверхности определяется поверхностной плотностью избыточного заряда σ. Выделим малый элемент поверхности dS ̄ заряженного проводника и применим теорему Гаусса. Поскольку элемент мал, то можно считать его плоским, а плотность заряда σ постоянной. Замкнутую поверхность ∑, охватывающую элемент, выберем в виде прямого цилиндра, основания которого перпендикулярны вектору dS ̄ – одно из них располагается вне тела на малом расстоянии от поверхности, а другое внутри. Поскольку вне проводника поле перпендикулярно поверхности, а внутри его просто нет, то поток вектора напряжённости вычисляется так: 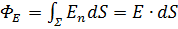. Полный заряд внутри поверхности ∑ равен произведению поверхностной плотности заряда σ на площадь поверхности элемента dS ̄. Поэтому по теореме Гаусса можем записать:

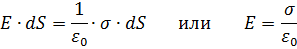
6. Плотность поверхностного заряда проводника зависит от её кривизны.

Заменим реальное проводящее тело произвольной формы (с различной кривизной поверхности) его грубой моделью. Пусть минимальная кривизна поверхности проводника характеризуется радиусом R ₁ , а максимальная R ₂ . Тогда наша модель будет состоять из двух проводящих шаров с радиусами R ₁ и R ₂ , соединённых тонкой проводящей проволокой. Если расположить шары далеко друг от друга, то можно считать, что избыточный заряд по их поверхности распределён равномерно. Запишем систему уравнений:

Подстановка первых двух соотношений в последнее равенство даёт:

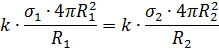
Откуда получаем:

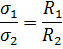
Поверхностная плотность заряда обратно пропорциональна радиусу кривизны поверхности:

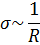
А также:

 

7. Электрический диполь. Поле диполя. «Элементарный диполь» во внешнем однородном и неоднородном электрическом поле.

(Опр.) Электрическим диполем называется система, состоящая из двух одинаковых по модулю и противоположных по знаку точечных зарядов q, находящихся на расстоянии l друг от друга.

Основной характеристикой диполя является его дипольный момент:

,

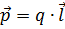где вектор l ̄, проведённый от отрицательного заряда к положительному, называется «плечом» диполя.

(Опр.) Элементарным диполем называется диполь микроскопических размеров.

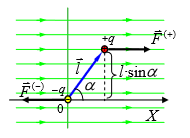· Однородное поле. Поскольку напряжённость такого поля одинакова во всех точках пространства, действующие на точечные заряды диполя q и -q силы F ̄⁽⁺⁾ и F ̄^(-) равны по величине и противоположны по направлению – результирующая сила равна нулю. Однако отличен от нуля момент этих сил, если только диполь не располагается вдоль силовых линий поля! Определим этот момент. Модуль момента сил относительно оси, перпендикулярной плоскости рисунка и проходящей через отрицательный заряд диполя:

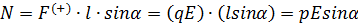
Вектор момента силы:

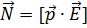
Итак, однородное электрическое поле оказывает на диполь ориентирующее действие, стремясь его повернуть, «выстраивая» вектор p̄ по направлению поля.

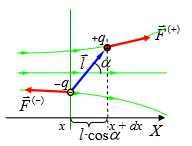· Неоднородное поле. В неоднородном поле помимо вращающего момента и сила, действующая на диполь, уже не равна нулю. Чтобы найти эту силу будем для начала считать, что поле изменяется лишь в одном направлении. Выберем в этом направлении координатную ось ОХ. Сложим проекции сил, действующих на каждый из точечных зарядов диполя:

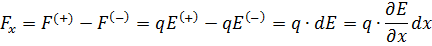
Здесь Е⁽⁺⁾ и Е^(-) – модуль напряжённости поля в месте нахождения +q и –q. Один заряд диполя смещён относительно другого вдоль оси ОХ на расстояние dx, равное lcosα. Проекцию силы можно записать в виде:

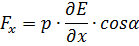
Если поле убывает в направлении оси ОХ, то знак проекции F_x отрицателен. Наоборот, если поле вдоль оси ОХ нарастает, то знак проекции положителен. В обоих случаях диполи втягиваются в область поля с большей напряжённостью!

В общем случае поле может изменяться при смещении в произвольном направлении, а его приращение равно

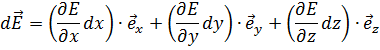
Действующая на диполь сила:

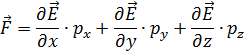
Общий вывод: Диполи ориентируются вдоль силовых линий и втягиваются в область поля с большей напряжённостью!

8. Проводники во внешнем электрическом поле. Свойства замкнутых проводящих оболочек (теоремы Фарадея).

При внесении проводника во внешнее электрическое поле в нём происходит перераспределение свободных заряженных частиц. Это явление называется «электростатической индукцией». В результате по поверхности оказывается распределён т.н. индуцированный заряд. На части поверхности проводящего тела находящейся ближе к положительно заряженным внешним телам концентрируются свободные электроны. На более удалённых частях поверхности возникает область, обеднённая этими частицами – т.е. они оказываются положительно заряженными.

Индуцированные заряды локализованы во внешнем поверхностном слое. Если удалить любую внутреннюю часть проводника, это никак не отразится на равновесии зарядов в проводнике и на электрическом поле внутри и вне него. То, что получается в этом случае, называется «проводящая оболочка».

---

Дата добавления: 2019-09-13; просмотров: 201; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!