Теорема об интегрировании по частям (доказать)
Задачи приводящие к понятию определенного интеграла. Понятие определенного интеграла, вычисление интеграла по определению. Необходимый признак интегрируемости (без док.)
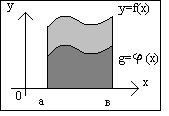
1) Задача о нахождении площади криволинейной трапеции.
Определение: криволинейная трапеция – плоская фигура ограниченная линиями 
, 
, 
, 
. 
-положительная и непрерывная на отрезке [a,b].
Разобьем промежуток [a;b] произвольно на n частей с длинами 
Получим n-криволинейную трапецию, основание 
, 
, 
.
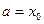построим прямоугольник с основанием и высотой 
.
, где (меняется от 1 до n)
(получим приближенное значение S криволинейной трапеции)
(Интегральная сумма)
2) Задача о вычислении длины пути по заданной скорости.
Пусть точка движется прямолинейно вдоль числовой оси 
, 
Смещение (.)-и за малые промежутки времени.
| Смещение
 ,
|
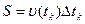1. Разобьем промежуток [a;b] произвольно на n частей с длинами
2. В каждом промежутке выберем точку (ξ) и вычислим значение функции в каждой из этих точек, получим значения (ξ)
3. Эти значения умножим на длины соответствующих промежутков , а полученные произведения сложим, получится сумма ∑:
которая называется интегральной суммой функции на данном промежутке
Определенным интеграломот функции у= на 
называется конечный предел соответствующей интегральной суммы при неограниченном увеличении числа разбиений промежутка на части (nàoo) и стремлении длин всех частичных промежутков к нулю (хi à0)
|
|
|
если предел конечен и не зависит от разбиений и выбора точки 
, где - подынтегральная функция.
-подынтегральное выражение.
а- нижний предел интегрирования.
в- верхний предел интегрирования.
d- длина наибольшего из отрезков разбиения.
Условие интегрируемости функций.
Необходимый признак интегрируемости функции. Если функция f(х) интегрируема на [a,b], то она ограничена на [a,b]. Следствие (достаточное условие интегрируемости):Если функция ограничена и непрерывна на [a,b], всюду кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке [a,b].
2. Свойства определенного интеграла. Теорема о среднем (без док.) Геометрический смысл. Среднее значение функции.
Основные свойства определенного интеграла.
Ø 
Ø 
Ø 
,где c-const, 
Ø Определенный интеграл от 
функций: 
Ø Адитивность определенногоинтеррала 
Ø Если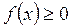 
, то 
Ø Монотонность определенного интеграла . если 
, то 
Ø Ограниченность. 
Ø Оценка определенного интеграла. Пусть f(х) интегрируема на [a,b], a<b, , 
|
|
|
Ø Теорема о среднем: Если f(х) непрерывна на [a,b], то существует точка 
, такая что 
, где 
-среднее значение.
3. Классы интегрируемых функций (три теоремы без док.)
Классы интегрируемых функций.
Теорема №1
Если определена на [a,в] и непрерывна, то интегрируема [a,в].
Теорема №2
Если функция монотонна и ограничена на [a,в], то интегрируема на [a,в].
Теорема №3
Если ограниченная функция на [a,в] имеет конечное число точек разрыва, то интегрируема на [a,в].
4. Теорема об определенном интеграле с переменным верхним пределом (доказать)
Теорема(Борроу): определенный интервал с переменным верхним пределом интегрирования от непрерывной функции f(x) на 
является первообразной для интегрируемой функции, т.е. 
Док-во: дадим аргументу х приращение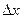 
,
тогда 
=>/ По Теореме о среднем / 
;
то 
т.д.
ГЕОМ.ИЛЛЮСТРАЦИЯ ТЕОРЕМЫ:
Приращение 
= 
= S криволинейной
трапеции с осями 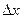, а производная 
=f(х)= длине отрезка х Х.
СЛЕДСТВИЕ: всякая непрерывная функция имеет первообразную.
5. Теорема Ньютона-Лейбница (доказать)
Теорема (Ньютона-Лейбница, формула) Если F(х)- есть какая-либо первообразная от непрерывной функции f(х), то справедлива формула: 
.
|
|
|
Док-во:
С одной стороны F(х) первообразная f(х). С другой стороны по Теореме об определенном интеграле с переменным верхним пределом, 
- первообразная f(х).
Но любые 2 первообразные от f(х) отличаются на постоянное слагаемое с=const.
Если х=а, то 
, но т.к. интеграл с одним пределом равен нулю, => 0=F(a)+C 
.
Если х=b,то 
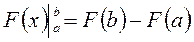,то 
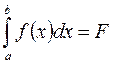т.д.
Замечание: Теорема справедлива и для кусочно-непрерывной функции
Теорема об интегрировании по частям (доказать)
Пусть U(x)и V(x) – имеют некоторые первообразные на [a,b], тогда 
Док-во: На [a,b] имеет место равенство (UV)’=U’V+UV’
(UV) – первообразная для непрерывной ф-ии (U’V+UV’), тогда по формуле Ньютона-Лейбница:
Дата добавления: 2019-09-13; просмотров: 321; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!