Геометрический смысл дифференциала.
 Из треугольника:
Из треугольника:  . Þ
. Þ  ,
,
где  — геометрический смысл производной.
— геометрический смысл производной.
Дифференциал – это приращение ординаты касательной, проведенной к кривой в точке касания x0.
Правила нахождения дифференциала.


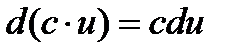

Применение дифференциала.
Приложение дифференциала к приближенным вычислениям.
Из рисунка видно, что приращение функции Dy и дифференциал dy связаны приближенным равенством Dy » dy. Поэтому с помощью дифференциала можно вычислять значения функции 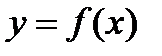 , если известно Dx (приращение):
, если известно Dx (приращение):  Þ
Þ  Þ
Þ  .
.
Пример: Вычислить приближенно  .
.
Введем функцию  . Значение x=1,004, берем значение
. Значение x=1,004, берем значение  .
.
 =
=  =1,
=1,  =1,004-1=0,004.
=1,004-1=0,004.
Вычислим дифференциал  =
=  =
=  =0,002,
=0,002,  =
=  =1+0,002=1,002.
=1+0,002=1,002.
Производные высших порядков.
Производная высших порядков.
Пусть функция 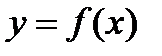 имеет производную в каждой точке некоторого интервала.
имеет производную в каждой точке некоторого интервала.  - также является функцией от x, следовательно, ее тоже можно продифференцировать.
- также является функцией от x, следовательно, ее тоже можно продифференцировать.  - производная второго порядка или вторая производная.
- производная второго порядка или вторая производная.  - производная третьего порядка или третья производная и т.д.
- производная третьего порядка или третья производная и т.д.  - производная n-порядка.
- производная n-порядка.
Обозначаются: y¢, y², y²¢, yIV или y(1), y(2), y(3), y(4)...
Пример:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Механический смысл второй производной.
Вторая производная есть ускорение a прямолинейного движения тела в данный момент времени, выражает зависимость пройденного пути от времени t, т.е. если  , то
, то  .
.
Уравнение касательной и нормали к кривой.
 Из пучка прямых, проходящих через точку
Из пучка прямых, проходящих через точку  , выберем одну прямую — касательную к графику функции:
, выберем одну прямую — касательную к графику функции:  . Из геометрического смысла производной угловой коэффициент касательной:
. Из геометрического смысла производной угловой коэффициент касательной:  .
.
Þ  .
.
Þ  – уравнение касательной.
– уравнение касательной.
Определение: Нормалью к кривой называется прямая, перпендикулярная к касательной, проведенной в точке касания с абсциссой x0.
Так как нормаль перпендикулярна к касательной, то угловой коэффициент нормали:  (из условия перпендикулярности прямых). Отсюда:
(из условия перпендикулярности прямых). Отсюда:  Þ
Þ 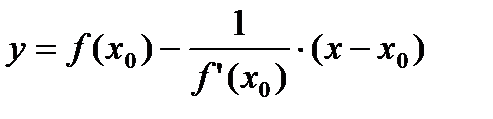 – уравнение нормали.
– уравнение нормали.
Пример: Составить уравнение касательной и нормали к графику функции  в точке с абсциссой равной 1.
в точке с абсциссой равной 1.
Ордината точки касания: 
Производная: 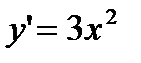 .
.
Найдем значение производной в точке x0: 
 ,
, 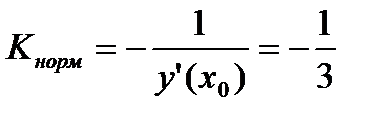
Уравнение касательной:  Þ
Þ 
Уравнение нормали:  Þ
Þ  .
.
Дата добавления: 2019-09-13; просмотров: 169; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
