Производная функции одной переменной.
 Определение: Пусть функция y=f(x) определена в точке x0 и некоторой ее окрестности. Дадим x0 приращение Dx так, чтобы точка
Определение: Пусть функция y=f(x) определена в точке x0 и некоторой ее окрестности. Дадим x0 приращение Dx так, чтобы точка  принадлежала указанной окрестности. Тогда функция получит приращение Dy.
принадлежала указанной окрестности. Тогда функция получит приращение Dy.  .
.
Если существует предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю, то он называется производной функции f(x) в точке x0.
 .
.
Обозначают производную  ,
,  , y',
, y',  ,
,  .
.
Замечание: Если изменить x0, то будет изменяться и производная функции в точке x0, следовательно, производная функции тоже является функцией.
Пример: Найти по определению производную функции y=x2.
Возьмем произвольную точку x, дадим приращение Dx, x®x+Dx. Функция получит приращение Dy:  =
=  =
= 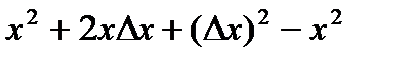 =
=  .
.
Рассмотрим предел  =
=  =
= 
Итак, производная  .
.
Связь между непрерывностью функции и существованием производной.
Теорема: Если функция имеет конечную производную в точке x0, то она непрерывна в этой точке.
Док-во:
По определению производной:  =
= 
Обозначим 
Тогда  .
.
По теореме о представлении функции, имеющей предел:
 , где
, где  ‒ б/м при
‒ б/м при  .
.



 при Δx→0.
при Δx→0.
По второму определению непрерывности, если б/м приращению аргумента соответствует б/м приращение функции, то  непрерывна в точке х0.
непрерывна в точке х0.
Ч.т.д.
Геометрический и физический смысл производной.
Геометрический смысл производной.
 На графике функции
На графике функции  возьмем точку М0 с координатами (x0,y0) и точку N с координатами (
возьмем точку М0 с координатами (x0,y0) и точку N с координатами (  ;
;  ). Проведем через эти точки секущую.
). Проведем через эти точки секущую.
|
|
|
| x0 |
x0+  x x
|
| y(x0+Dx) |
| y0=y(x0) |
 в точке M0(x0,y0) называется предельное положение секущей M0N, когда точка N стремится к точке M0 по графику.
в точке M0(x0,y0) называется предельное положение секущей M0N, когда точка N стремится к точке M0 по графику.
С одной стороны tga является угловым коэффициентом секущей, с другой стороны из прямоугольного треугольника:  .
.
 Когда точка N®M по графику, тогда приращение
Когда точка N®M по графику, тогда приращение
аргумента Dx®0, при этом угловой коэффициент
касательной  .
.
Переходя к пределу при  ,
,
получаем  .
.
Геометрический смысл производной заключается в следующем: производная функции в точке x0 равна угловому коэффициенту касательной, проведенной к графику функции в точке с абсциссой x0.
 .
.
Физический смысл производной.
Пусть материальная точка движется прямолинейно по закону S=S(t), где t ‒ время, S — координата точки на оси.
Физический смысл производной заключается в следующем: Производная – это мгновенная скорость изменения функции.
Vмгн=S'(t).
Правила вычисления производной.
1.  .
.
Док-во:
Дадим x приращение Dx,  . Тогда функция получит приращение Dy. Отсюда
. Тогда функция получит приращение Dy. Отсюда  . Так как
. Так как  , то
, то  . Þ (C)¢=0.
. Þ (C)¢=0.
Ч.т.д.
2. Если функции u и v имеют конечные производные, то производная суммы (разности) равна сумме (разности) производных:  .
.
|
|
|
Док-во:
Дадим x приращение Dx,  . Тогда функция
. Тогда функция  получит приращение
получит приращение  . Отсюда
. Отсюда  =
=  =
= 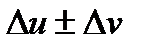 .
.
Þ  =
= 

 =
=  .
.
Ч.т.д.
3. Если функции u и v имеют конечные производные, то производная произведения находится по формуле:  .
.
Доказывается аналогично второму.
Следствие: Константу можно выносить за знак произведения:  .
.
4. Если функции u и v имеют конечные производные, то производная частного находится по формуле:  , где v¹0.
, где v¹0.
Таблица простейших производных.
| Степенные функции | |||

| 
| 
| 
|
| Показательные функции | Логарифмические функции | ||

| 
| 
| 
|
| Тригонометрические функции | |||

| 
| 
| 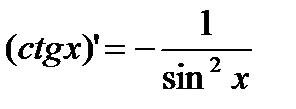
|
| Обратные тригонометрические функции | |||

| 
| 
| 
|
Дата добавления: 2019-09-13; просмотров: 161; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
