Задание 13. Вычисление длины дуги кривой, заданной параметрическими уравнениями.
Длина дуги кривой, заданной параметрическими уравнениями, вычисляется по формуле:
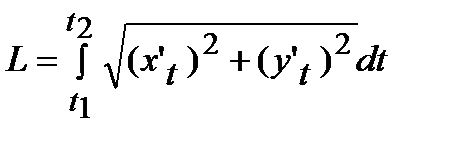 .
.
Замечание. При вычислении длины кривой, заданной параметрическими уравнениями, нижний предел интегрирования должен быть меньше верхнего предела интегрирования.
Пример. Вычислить длину дуги астроиды, заданной уравнениями:
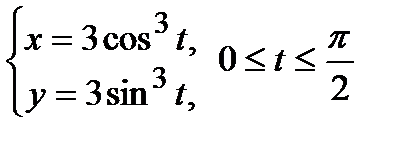 .
.
Решение.
Вычислим производные функций:
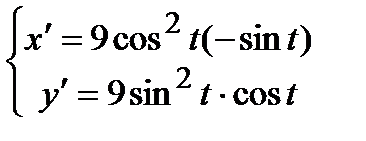 .
.
Вычислим подынтегральную функцию:
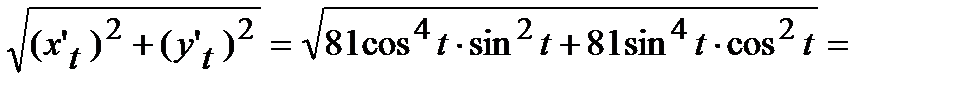
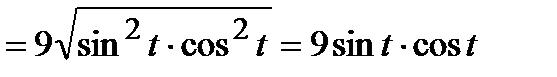 .
.
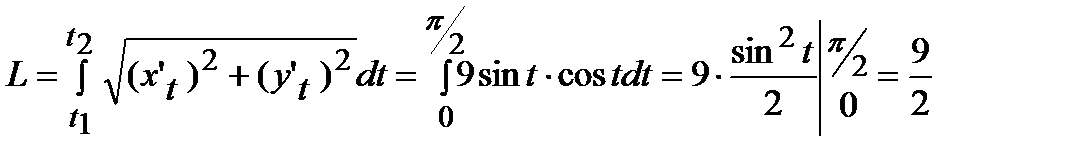 .
.
Следовательно, длина дуги 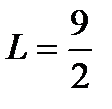 (ед.).
(ед.).
Задание 14. Вычисление объема тела, образованного вращением фигуры, ограниченной линиями в декартовых координатах.
Пусть дана криволинейная трапеция, ограниченная линиями 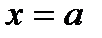 ,
, 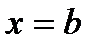 ,
, 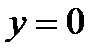 ,
, 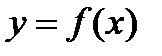 , где
, где 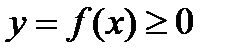 - непрерывная функция. Если ее вращать вокруг оси абсцисс, то получим тело вращения (рис.7), объем которого вычисляется по формуле:
- непрерывная функция. Если ее вращать вокруг оси абсцисс, то получим тело вращения (рис.7), объем которого вычисляется по формуле:
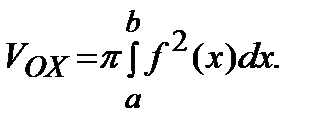
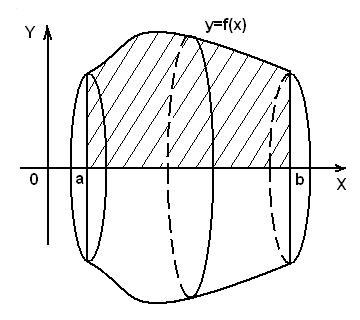
Рис.7
Если криволинейную трапецию, ограниченную линиями 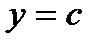 ,
, 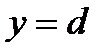 ,
, 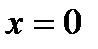 ,
, 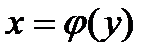 , где
, где 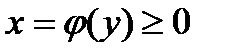 - непрерывная функция, вращать вокруг оси ординат, то получим тело вращения (рис.8), объем которого вычисляется по формуле:
- непрерывная функция, вращать вокруг оси ординат, то получим тело вращения (рис.8), объем которого вычисляется по формуле:
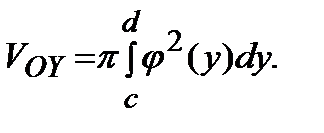
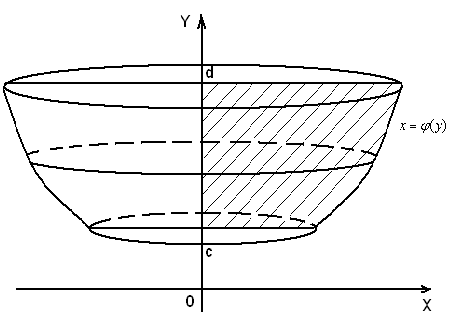
Рис.8
Пусть дана криволинейная трапеция, ограниченная линиями 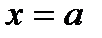 ,
, 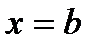 ,
, 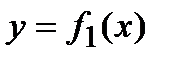 ,
, 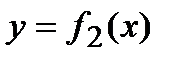 , где
, где 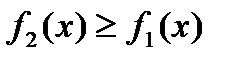 (рис.9), то объем полученного тела вращения вычисляется по формуле:
(рис.9), то объем полученного тела вращения вычисляется по формуле:
 .
.
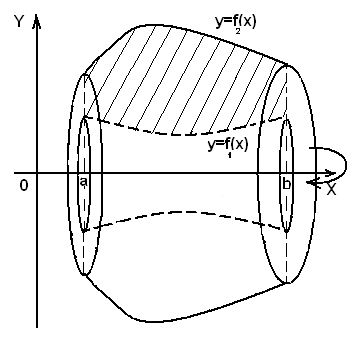
Рис.9
Пример. Криволинейная трапеция, ограниченная осью абсцисс и кривой 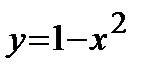 вращается вокруг оси
вращается вокруг оси 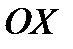 . Найти объем полученного тела вращения.
. Найти объем полученного тела вращения.
Решение. На рис.10 изображена криволинейная трапеция, которая вращается вокруг оси 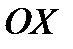 .
.
|
|
|
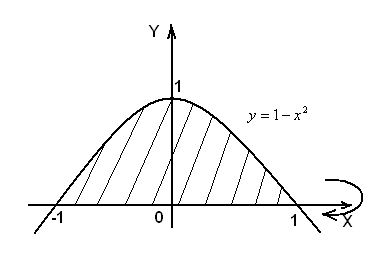
Рис.10
Точки пересечения кривой 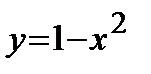 с осью
с осью 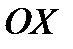 :
: 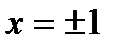 .
.
Следовательно, пределы интегрирования: 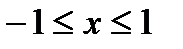 .
.
Искомый объем тела вращения:
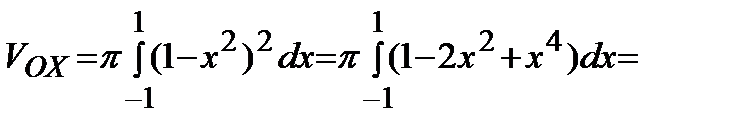
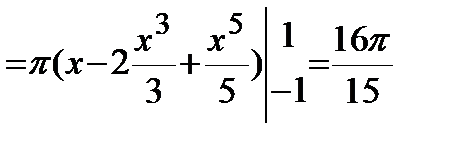 (куб.ед.).
(куб.ед.).
Пример. Криволинейная трапеция, ограниченная осью ординат и кривой  вращается вокруг оси
вращается вокруг оси 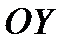 . Найти объем полученного тела вращения.
. Найти объем полученного тела вращения.
Решение. На рис.11 изображена криволинейная трапеция, которая вращается вокруг оси 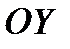 .
.
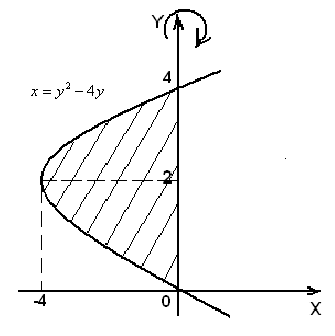
Рис.11
Кривая 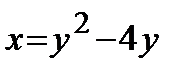 — это парабола с вершиной (-4;2), которая пересекает ось ординат в точках
— это парабола с вершиной (-4;2), которая пересекает ось ординат в точках 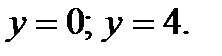
Следовательно, пределы интегрирования: 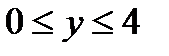 .
.
Искомый объем тела вращения:
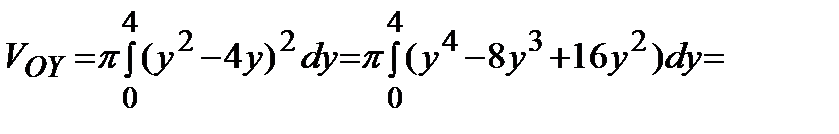
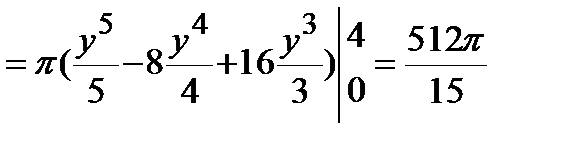 (куб. ед.).
(куб. ед.).
Пример. Фигура, ограниченная линиями 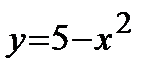 и
и 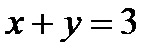 ,вращается вокруг
,вращается вокруг 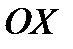 . Найти объем полученного тела вращения.
. Найти объем полученного тела вращения.
Решение. На рис.12 изображена фигура, которая вращается вокруг оси 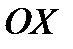 .
.
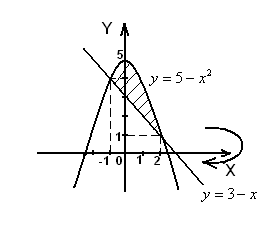
Рис.12
Точки пересечения параболы 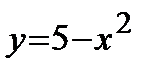 и прямой
и прямой 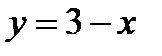
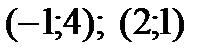 .
.
Следовательно, пределы интегрирования: 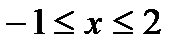 .
.
Искомый объем тела вращения вычислим по формуле:
 .
.
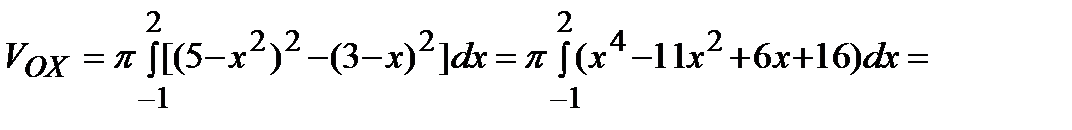
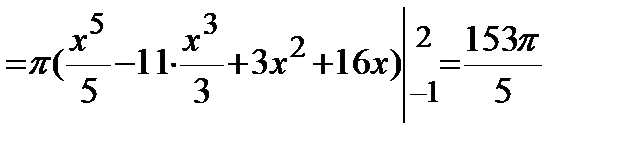 (куб. ед.).
(куб. ед.).
НЕСОБСТВЕННЫЙ ИНТЕГРАЛ
Задание 15. Сходимость несобственного интеграла.
Несобственные интегралы по бесконечному промежутку.
Пусть функция 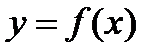 непрерывна на промежутке
непрерывна на промежутке 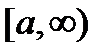 , тогда очевидно, что при любом
, тогда очевидно, что при любом 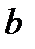 имеет смысл интеграл
имеет смысл интеграл 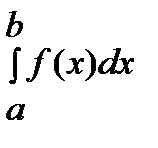 . Будем расширять промежуток
. Будем расширять промежуток 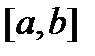 , увеличивая
, увеличивая 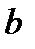 . Тогда, если существует предел:
. Тогда, если существует предел: 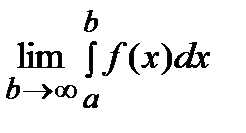 , то этот предел называется несобственным интегралом от функции
, то этот предел называется несобственным интегралом от функции 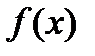 по бесконечному промежутку
по бесконечному промежутку 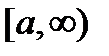 и обозначается:
и обозначается: 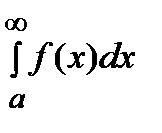 .
.
|
|
|
Отметим, что если указанный предел существует и конечен, то интеграл 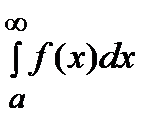 называется сходящимся, в противном случае – расходящимся.
называется сходящимся, в противном случае – расходящимся.
Пример. Выяснить сходимость несобственного интеграла 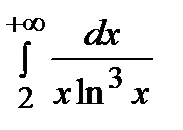 .
.
Решение.
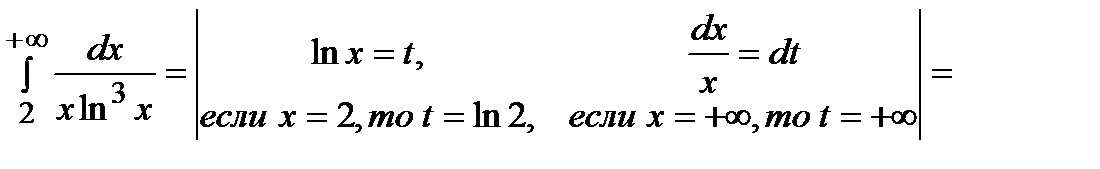
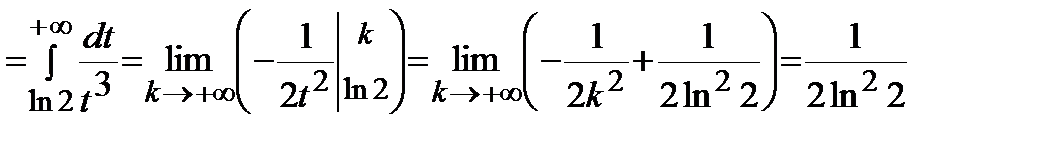 .
.
Следовательно, исходный интеграл – сходится.
Дата добавления: 2019-09-13; просмотров: 249; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
