Методические указания к выполнению индивидуальных домашних заданий
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Функция 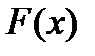 называется первообразной функции
называется первообразной функции 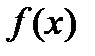 на некотором интервале
на некотором интервале 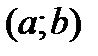 , если
, если 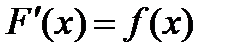 для всех значений
для всех значений 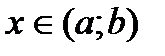 . Если
. Если 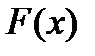 — первообразная
— первообразная 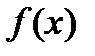 , то очевидно, что бесконечное множество всех первообразных
, то очевидно, что бесконечное множество всех первообразных 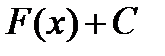 , отличающихся только константой, также будет первообразной
, отличающихся только константой, также будет первообразной 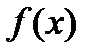 . Множество всех первообразных функций
. Множество всех первообразных функций 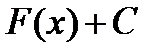
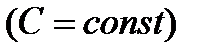 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 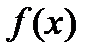 и обозначается
и обозначается 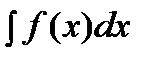 . При этом
. При этом 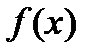 называется подынтегральной функцией,
называется подынтегральной функцией, 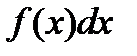 — подынтегральным выражением,
— подынтегральным выражением, 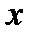 — переменной интегрирования.
— переменной интегрирования.
Согласно вышеприведенному:
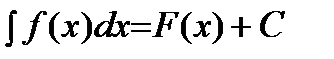 ,
,
где 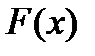 — некоторая первообразная функции
— некоторая первообразная функции 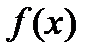 ;
; 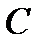 — произвольная постоянная.
— произвольная постоянная.
Неопределенный интеграл обладает следующими свойствами:
1) 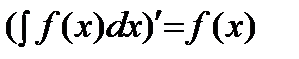 .
.
2) 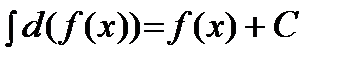 .
.
3) 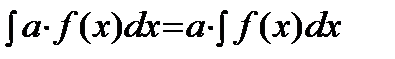 , где
, где 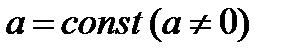 .
.
4) 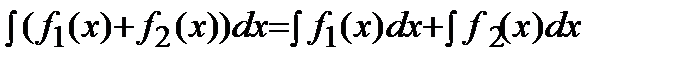 .
.
5) 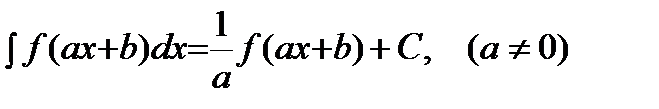 .
.
Таблица основных неопределенных интегралов:
1) 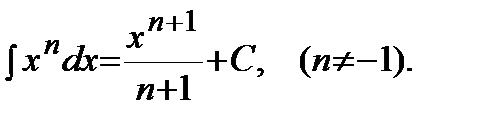
| 2) 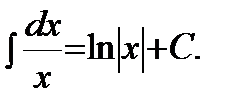
|
3) 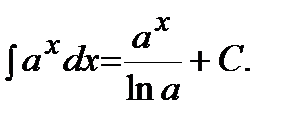
| 4) 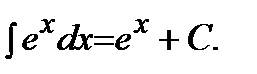
|
5) 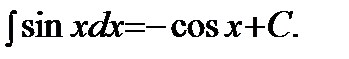
| 6) 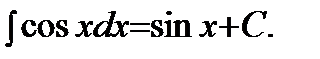
|
7) 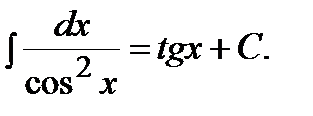
| 8) 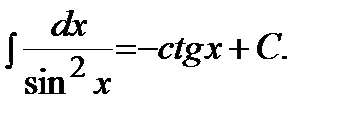
|
9) 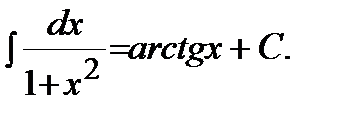
| 10) 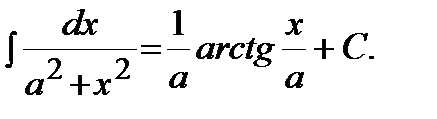
|
11) 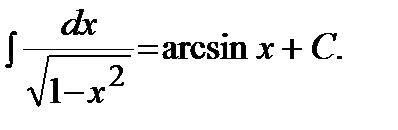
| 12) 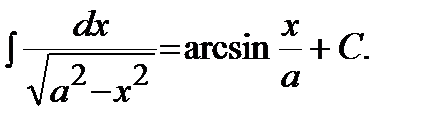
|
13) 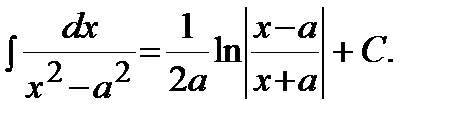
| 14) 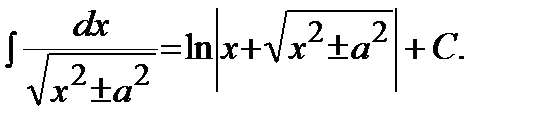
|
Основные методы интегрирования.
Задание 1. Непосредственное интегрирование.
Непосредственное интегрирование предполагает использование свойств неопределенного интеграла, таблицы интегралов и различных формул из элементарной математики.
Пример. 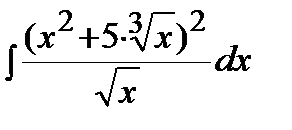 .
.
Решение. Воспользуемся формулой сокращенного умножения (квадрат суммы), свойствами степеней, свойствами 3-4 и формулой 1 таблицы интегралов:
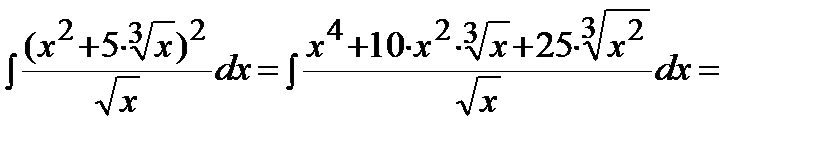
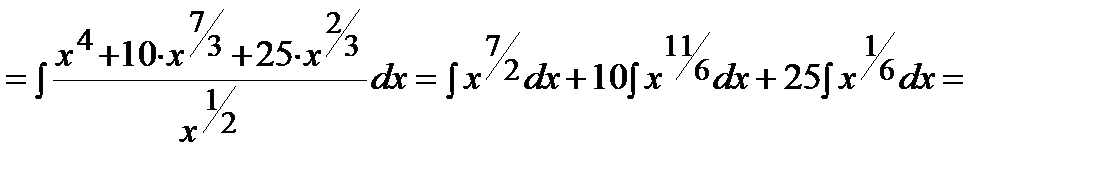
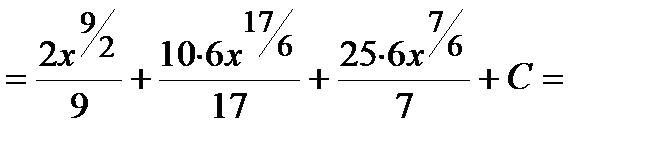
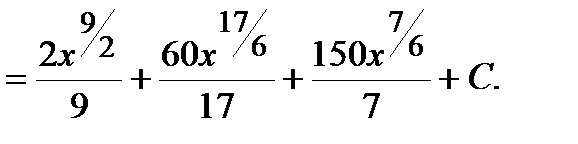
Пример. 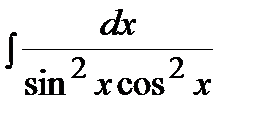 .
.
Решение. Преобразуем подынтегральную функцию:
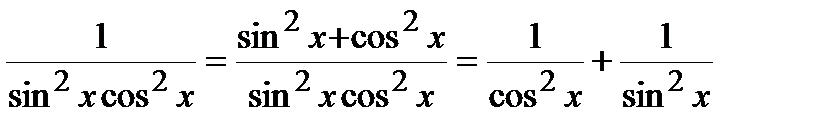 .
.
Следовательно, используя формулы 7 и 8 таблицы интегралов, получим:
|
|
|
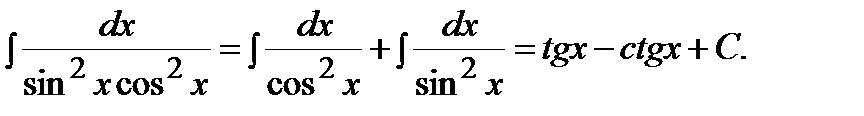
Пример. 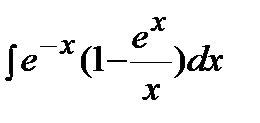 .
.
Решение. Преобразуем подынтегральную функцию, раскрыв скобки, и воспользуемся формулами 2 и 4 таблицы интегралов:
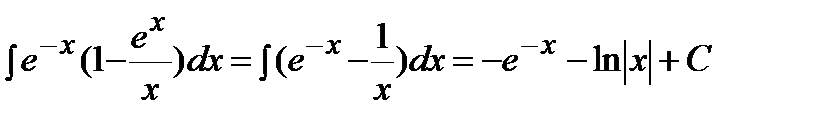 .
.
Задание 2. Интегралы с квадратным трехчленом.
Интегралы с квадратным трехчленом - это интегралы вида: 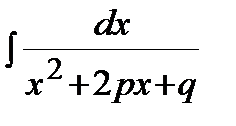 ,
, 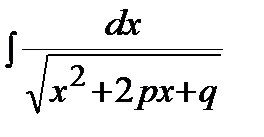 ,
, 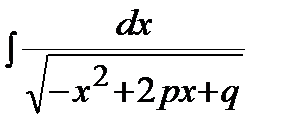 .
.
Для вычисления этих интегралов необходимо выделить в квадратных трехчленах знаменателей полный квадрат. В первых двух случаях квадратный трехчлен перепишется в виде: 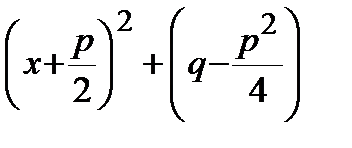 , в третьем случае он будет иметь вид:
, в третьем случае он будет иметь вид: 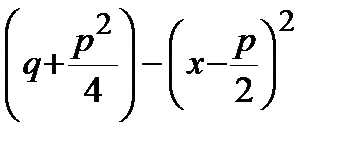 . В результате интегралы сводятся к табличным интегралам.
. В результате интегралы сводятся к табличным интегралам.
Замечание. Если коэффициент при 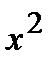 в квадратных трехчленах не равен 1, то его предварительно нужно вынести за знак интеграла.
в квадратных трехчленах не равен 1, то его предварительно нужно вынести за знак интеграла.
Пример. 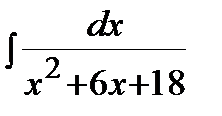 .
.
Решение. Выделим полный квадрат в знаменателе и воспользуемся формулой 10 таблицы интегралов:
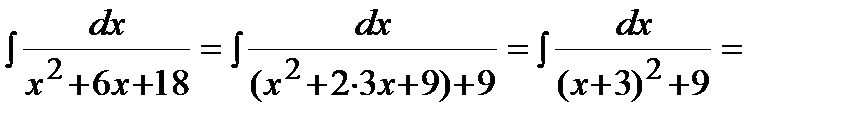
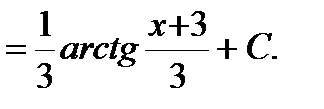
Пример. 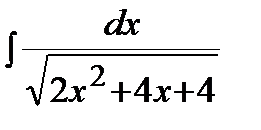 .
.
Решение. Выделим полный квадрат в подкоренном выражении и воспользуемся формулой 14 таблицы интегралов: 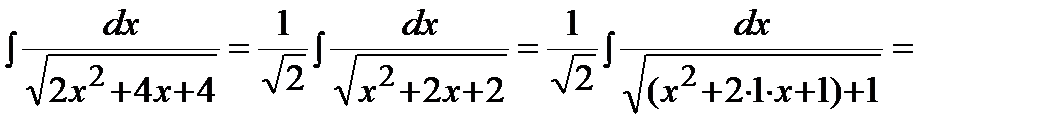
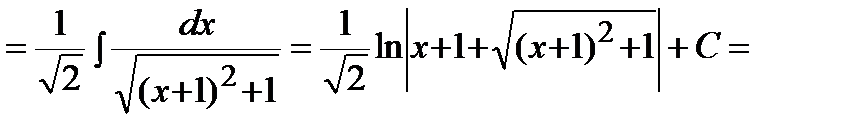
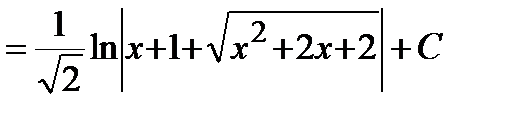 .
.
Пример . 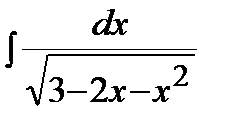 .
.
Решение. Выделим полный квадрат в подкоренном выражении и воспользуемся формулой 12 таблицы интегралов:
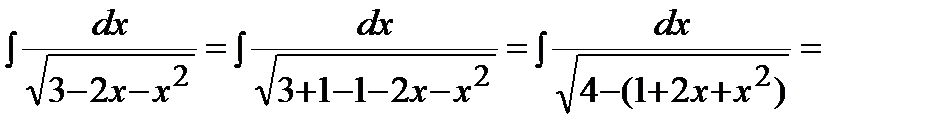
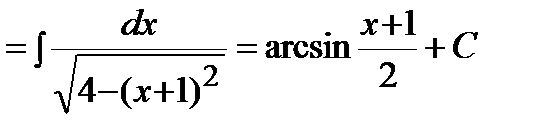 .
.
Задание 3. Замена переменной.
Пусть требуется найти интеграл с непрерывной подынтегральной функцией 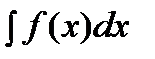 .
.
Сделаем замену переменных, положив 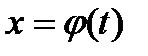 , где функция
, где функция 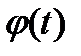 удовлетворяет следующим двум условиям:
удовлетворяет следующим двум условиям:
|
|
|
1) 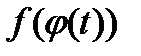 - непрерывная функция;
- непрерывная функция;
2) 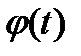 - непрерывно дифференцируемая функция, имеющая обратную функцию.
- непрерывно дифференцируемая функция, имеющая обратную функцию.
Тогда 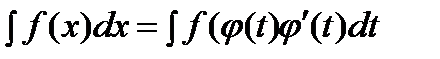 .
.
После интегрирования возвращаются к старой переменной обратной подстановкой.
Пример. 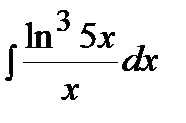 .
.
Решение.
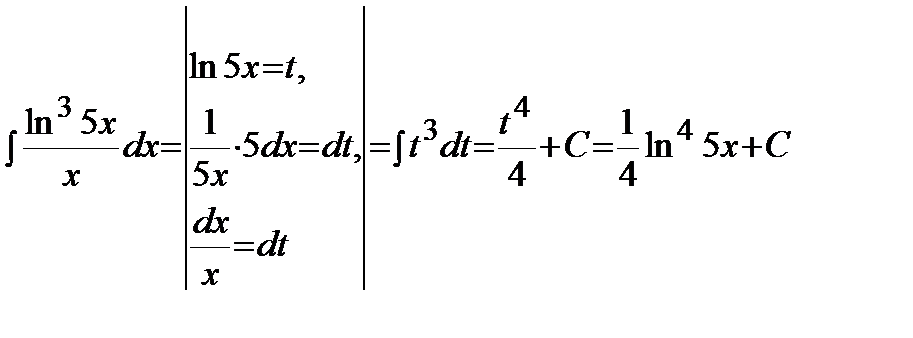 .
.
Пример. 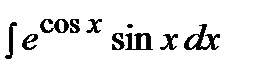 .
.
Решение.
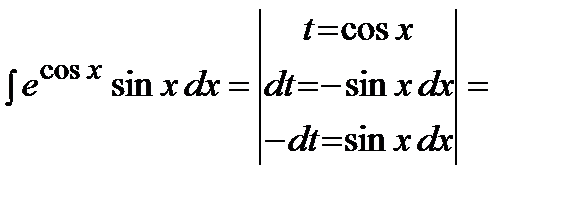
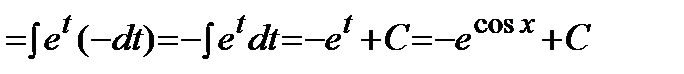 .
.
Пример. 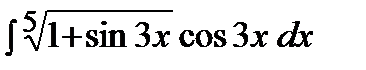 .
.
Решение.
Полагая 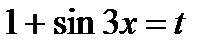 и продифференцировав обе части этого равенства, получаем:
и продифференцировав обе части этого равенства, получаем:
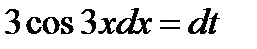 или
или 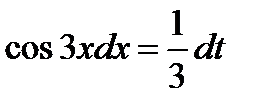 .
.
Тогда первоначальный интеграл равен:
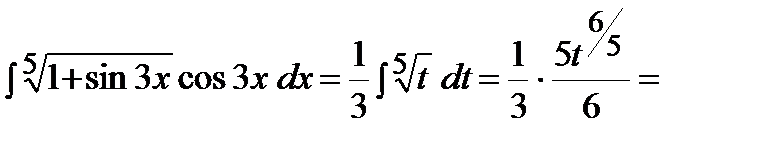
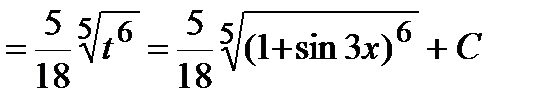 .
.
Пример. 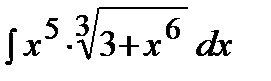 .
.
Решение.
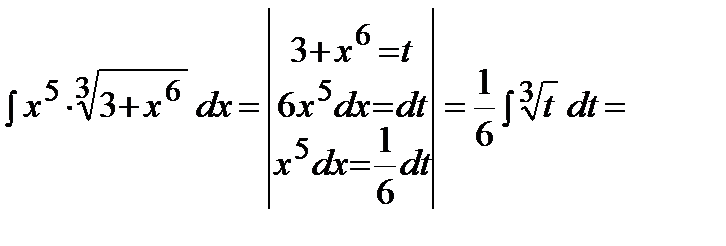
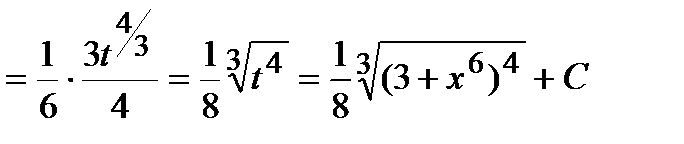 .
.
Дата добавления: 2019-09-13; просмотров: 169; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
