МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛОРУССКИЙ НАЦИОНАЛБНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Факультет МСФ
Кафедра «Детали машин, ПТМ и М»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту
по дисциплине механика
Тема:«Механический привод»
Исполнитель: Тригубович Татьяна
Сергеевна
студентка 2 курса 106526 группы
Руководитель проекта: доцент Статкевич Александр Михайлович
Минск 2008
Расчёт валов по эквивалентному моменту
Нагрузка валов редуктора
Редукторные валы испытывают два вида деформации - изгиб и кручение. Деформация кручения на валах возникает под действием вращающих моментов, приложенных со стороны двигателя и рабочей машины. Деформация изгиба валов вызывается силами в зубчатом зацеплении закрытых передач и консольными силами со стороны открытых передач и муфты.
Определение сил в зацеплении закрытых передач
В данном проектируемом приводе конструируется цилиндрический шевронный редуктор с углом наклона и углом зацепления  . За точку приложения сил принимают полюс зацепления в средней плоскости колеса.
. За точку приложения сил принимают полюс зацепления в средней плоскости колеса.
Значения сил определяем по табл. 6.1 [1].
На колесе:
окружная сила

радиальная сила

осевая сила.

На шестерне:
окружная сила, 
радиальная сила, 
осевая сила  .
. 
Определение консольных сил
 В проектируемом приводе конструируется открытая передача, которая определяет консольную нагрузку на выходной конец вала шестерни. Консольная сила от плоскоременной передачи
В проектируемом приводе конструируется открытая передача, которая определяет консольную нагрузку на выходной конец вала шестерни. Консольная сила от плоскоременной передачи  перпендикулярна оси вала и лежит в вертикальной плоскости вместе с радиальной силой
перпендикулярна оси вала и лежит в вертикальной плоскости вместе с радиальной силой 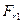 . Значение этой консольной нагрузки определяем по табл. 6.2 [1]:
. Значение этой консольной нагрузки определяем по табл. 6.2 [1]:
 , где
, где
 - сила предварительного натяжения ремня, Н,
- сила предварительного натяжения ремня, Н,
 - угол обхвата ремнем ведущего шкива, град.
- угол обхвата ремнем ведущего шкива, град.
Кроме того, консольная нагрузка вызывается муфтой, соединяющей редуктор с рабочей машиной. Консольная сила от муфты  перпендикулярна оси вала и лежит в горизонтальной плоскости вместе с окружной силой
перпендикулярна оси вала и лежит в горизонтальной плоскости вместе с окружной силой  .
.
 Значение определяется по табл. 6.2 [1]:
Значение определяется по табл. 6.2 [1]:

Расчет ведущего вала
Для удобства вычислений расстояния между основными точками вала обозначим латинскими буквами:
a=84
b=65
c=64
а) определяем опорные реакции в вертикальной плоскости:

Проверка:

б) строим эпюру изгибающих моментов относительно оси Х в характерных сечениях 1..4:
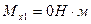




в) Определяем опорные реакции в горизонтальной плоскости
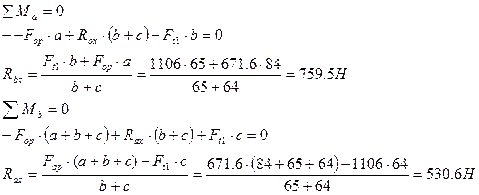
Проверка

г) строим эпюру изгибающих моментов относительно оси Y в характерных сечениях 1..4:




Строим эпюру крутящих моментов

Определяем суммарные радиальные реакции:


Строим эпюру суммарных изгибающих моментов:
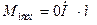



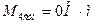
Расчет ведомого вала

а) определяем опорные реакции в вертикальной плоскости:

Проверка:

б) строим эпюру изгибающих моментов относительно оси Х в характерных сечениях 1..4:



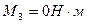
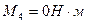
) Определяем опорные реакции в горизонтальной плоскости:

Проверка:

г) строим эпюру изгибающих моментов относительно оси Y в характерных сечениях 1..4:

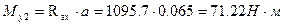
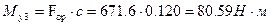


Строим эпюру крутящих моментов

Определяем суммарные радиальные реакции:
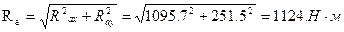

Строим эпюру суммарных изгибающих моментов:




Дата добавления: 2019-09-02; просмотров: 230; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
