Застосування інформатики для рішення проблем математичних більярдів
Комп’ютерний, або обчислювальний експеримент дозволяє без особливих розумових зусиль розглянути досить складні явища і скласти якісь уявлення про них. З розповсюдженням комп’ютерної техніки такі експерименти проникають в багато галузей людської діяльності. З обчислювальних досліджень більярдів існує десятки наукових робіт.
Як робиться обчислювальний експеримент? Обирається точка z0 і будується більярдна траєкторія, що виходить з неї. Програма видає наступну (після z0 ) точку віддзеркалення z1 € М , потім точку другого віддзеркаленні і так далі. Важливо, щоб фазовий циліндр М містив інваріантні криві (незмінні при перетвореннях).
Для ілюстрації наведемо результат обчислювального експерименту французьких дослідників А. Хелі і Т. Дюмона. Вони прорахували більярд в області, обмеженій двома дугами AD і ВС більшого радіусу і двома дугами AB і CD – меньшого радіусу. В такій побудові виділяють 10 інваріантів. Це ілюструє малюнок, приведений нижче.
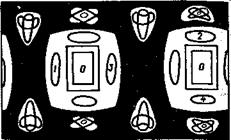
Математичний більярд в силовому полі
Математичний більярд - відома задача, розв'язується аналітично звичайно на прямокутному "столі". Аналітичне ж рішення задачі математичного більярда в силовому полі (наприклад, в полі сили тяжкості) на "столах", що мають різні форми, вельми скрутно. Графічне представлення траєкторій руху абсолютно пружного тіла (без урахування опору середовища) може бути отримано за допомогою комп'ютера.
|
|
|
На мал. 1 - 5 представлені траєкторії руху тіл на столі з параболічним бортом. На мал. 1 - тіло рухається в полі з 
, з початковою швидкістю, рівною нулю. Таке ж сімейство кривих виходить для випадків руху тіл, кинутих "під кутом до горизонту", якщо перший удар об стінку буде справа. В осоружному випадку, траєкторії матимуть інший вигляд - мал. 3, які вироджуються у відрізок параболи, якщо перший удар відбувається під кутом 90 0 . На цих малюнках чітко видні "заборонені зони".
На рис.4 представлений випадок повернення в початкову крапку після 14 ударів об параболічний борт.
На рис.5 зображено сімейство кривих - траєкторія руху тіла з крапки А 1 з невеликої відстані від параболічного борту.
На мал. 6 - 8 зображені траєкторії руху тіла у кута борту з різними кутами розчину - 90 0 (рис.6), 60 0 (мал. 8) і - менше 90° (мал. 7).
Чітко видна "заборонена зона" на рис. 8.
1. Задача повинна займати важливе місце в курсі фізики; 2. спираючись на вивчений матеріал, повинна містити нові елементи 3. носити узагальнений характер, щоб можна було вирішувати великий клас задач по вибраній темі; 4. математичний апарат повинен бути найпростішим з можливих, але не шкодити строгості математичної моделі.
|
|
|
Робота з пакетом Derive
Оголосимо спочатку в пакеті Derive невеличку бібліотеку допоміжних функцій для розв’язування деяких стандартних задач аналітичної геометрії.
#1: SYM_Z(p, c) := 2·c – p
Функція SYM_Z(P, C) повертає образ точки P при симетрії відносно точки C. Наступна функція SYM_L(P, A, q) повертає образ точки P при симетрії відносно прямої, що проходить через точку A паралельно вектору q.
Функція SYM_PL(P, A, B) повертає образ точки P при симетрії відносно прямої AB.
Функція SYM_PL(P, A, B) повертає образ точки P при симетрії відносно прямої AB.
Значенням функції PR(v) є вектор, що одержується із вектора v при повороті на 90°.
Оголосимо тепер функцію SOL2(m, n, p, q), що повертає розв’язок системи векторних рівнянь
Функція INTERSECT(A, B, C, D) повертає точку перетину прямих AB і CD.
LINE1(n, r0, r) — пряма, що проходить через точку r0 перпендикулярно вектору n (r — радіус-вектор довільної точки прямої); LINE2(q, r0, r) — пряма, що проходить через точку r0 паралельно вектору q; Оголосимо тепер функцію BIL2(K, L, A, B, C) , яка повертає вектор, елементами якого є дві точки, що задають відбитий промінь. Функція REPLACELAST(u, v) вилучає останній елемент вектора u і дописує в кінець одержаного вектора елементи вектора v.
|
|
|
Тепер ми можемо випробувати нашу програму на практиці. Розглянемо більярд у трикутнику з вершинами (2; 2), (5; 6), (8; 2). Спочатку побудуємо сам трикутник.
#22: [[2, 2], [5, 6], [8, 2],[2, 2]]
Побудуємо більярдну траєкторію, що задається точкою (3; 2) та вектором (0; 1).
#23: BIL([3, 2], [0, 1], [1, 1], [4, 5], [7, 1], 4)
Після спрощення виразу #23, одержимо:
#24: [[3, 2], [3, 11/3], [181/39, 485/117], [1389/527, 1], [1837/975, 6373/2925], [1037/175, 1]]
Результат побудови зображено на рис.2.
Збільшимо кількість вершин більярду.
#25: BIL([3, 2], [0, 1], [1, 1], [4, 5], [7, 1], 100)
#26: [[3, 2], [3, 11/3], [181/39, 485/117], [1389/527, 1], [1837/975, ...
Результат побудови виразу #26 (рис.3) на перший погляд може здатися неправдоподібним, оскільки наш більярд повинен містити 101ланку. Що ж це означає?
Наша більярдна траєкторія періодична! Це означає, що траєкторія через деякий час попаде в початкову точку Р(3; 2) і матиме в цій точці напрям v(0; 1). Очевидно, що далі точка буде повторювати попередню траєкторію. Траєкторія двічі зустрічається з основою трикутника під прямим кутом і змінює напрям руху на протилежний. Неважко переконатися, що побудована періодична траєкторія має 98 вершин.
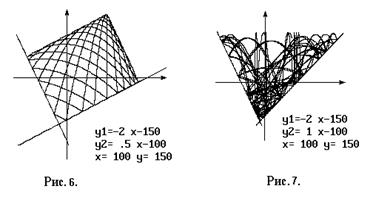
Як і очікувалося більярдна точка після трьох зіткнень зі сторонами трикутника не влучила у вершину і продовжила свій шлях у трикутнику (рис.5). На рисунку 6 наведено збільшене зображення околу вершину трикутника, а на рисунку 7 зображено перші 500 ланок того ж самого більярда.
|
|
|
Рисунок 5
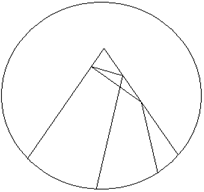
Рисунок 6
Рисунок 7
За допомогою цієї програми можна створювати такі цікаві траєкторії, як показані на малюнку, наведеному нижче.
Висновок
В результаті проведеної роботи, зазначеної у вступі, були отримані такі висновки:
Хоча математичний більярд – достатньо молода теорія, але в останній період вона здобула широке визнання. Основну роль в бурхливому розвитку цієї теорії відіграє застосування комп’ютерних програм для моделювання ситуацій розташування траєкторій. В практичній частині яскраво показано доцільність вивчення елементів теорії математичних більярдів, а саме «методу випрямлень» і побудові траєкторій в опуклих гладких областях, в школі на факультативах з математики. Дуже цікавими виявились правила гри в дійсний більярд, що витікають з математичної теорії. Це можна застосовувати для проведення нетрадиційних уроків з математики. Важливі висновки були зроблені при розробках комп’ютерної програми для побудови більярдних траєкторій. На наглядному прикладі використання математичних відомостей було продемонстровано використання математичних правил в фізичних дослідженнях.
Отримані висновки свідчать про широкі можливості застосування теорії. Як зауваження, хотілось би запропонувати введення елементів теорії математичних більярдів в курс геометрії в вищих спеціалізованих навчальних закладах, поряд з вивченням теми Симетрія. На доданках 1 і 2 запропоновані задачі для самостійної роботи студентів другого курсу спеціальності «математика».
Отже, можна підбити висновки і на основі вищезазначеного стверджувати, що поставлена в вступній частині мета в ході роботи була досягнена.
Список джерел
1. Балін І.В. В мире бильярда – Ростов н/д: «Фенікс», 2001.
2. Біркгоф Г. Динамические системы. – М.,: Л.:ОГИЗ, 1941
3. Гальперін Г.О. Биллиарды и хаос – М.:Знание, 1991.
4. Гальперін Г.О., Земляков О.М. Математические бильярды –М.:Наука, 1990. //Библиотечка «Квант», вып.77.
5. Гальперін Г.О., Стьопін А.М. Периодические движения бильярдного шара – Квант, 1989, № 3.
6. Земляков А.Н. Бильярды и поверхности. –Квант, 1979, №9.
7. Земляков А.Н. Математика бильярда. – Квант, 1976, №5.
8. Коріоліс Г.Г. Математическия теория бильярдной игры. – М.: Гостехиздат, 1956
9. Лазуткін В.Ф. Выпуклый биллиард и собственные функции оператора Лапласа – С.-П.: Изд-во ЛГУ, 1981
10. Раков С.А. Комп’ютерне моделювання трикутного математичного більярду // Комп’ютер у школі та сім’ї. — 2005. — №1. — C. 42–47.
11. Сінай Я.Г. Бильярдные траектории в многогранном угле // Успехи математических наук. – 1978. – Т.33. – Вып.1. – с.291-300.
12. Сінай Я.Г. Динамические системы с упругим отражениями. Эргодические свойства рассеивающихся биллиардов. //Успехи математических наук, 1970, т. 25, вып 2.
13. Совертков П.И. Занимательное компьютерное моделирование в элементарной математике: Учебное пособие. – М.: Гелиос АРВ, 2004. – 384 с.
Дата добавления: 2019-09-02; просмотров: 180; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!