Испытание на крип (ползучесть).

⇐ ПредыдущаяСтр 2 из 11Следующая ⇒

Если материал долгое время находится под нагрузкой, то под воздействием постоянного напряжения он может непрерывно деформироваться, даже несмотря на то, что величины действующих на него напряжений значительно ниже предела упругости. Эта деформация материала, зависящая от времени его нахождения под нагрузкой, называется крипом, который, в конечном итоге, ведет к разрушению материала. В частности, понимание этого явления важно, если материал используют при температурах, превышающих половину значения температуры плавления или температуры размягчения, что, например, характерно для некоторых амальгамных фаз или многих пластических материалов. При температурах на 40 — 50% меньше абсолютной точки плавления материала, крип ничтожно мал.

1. К каким группам относятся материалы, диаграммы которых представлены на рисунках а, б и в?

а – диаграмма образца из малоуглеродистой стали (ст3); б – диаграмма растяжения чугуна; в – диаграмма растяжения образца из легированной стали.

2. Указать основные характеристики прочности на диаграмме растяжения в варианте а?

1 – участок, в котором справедлив закон Гука и деформация является пластической;

2 – участок предела упругости, на котором напряжение достигает значения, при котором пластическая деформация достигает малой нормированной величины; 3 – площадка текучести, при этом напряжении происходит удлинение тела; 4 – временное сопротивление, на этом участке напряжение характеризует максимальную несущую способность материала, его прочность, предшествующую разрушению.

1. Что такое статический момент сечения?

Статическим моментом площади плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений элементарных площадок на расстояния от них до этой оси.
2. Что такое осевой и центробежный моменты инерции плоского сечения?

Осевой момент инерции фигуры – это интеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси. Формулы осевого момента инерции произвольной фигуры относительно осей x и y:

Центробежный момент инерции фигуры – это интеграл произведений элементарных площадей на их расстояния до осей x и y:

3. Изменяются ли центробежные и осевые моменты инерции при повороте осей? При параллельном переносе?

Если оси координат поворачивать в своей плоскости вокруг начала координат, то полярный момент инерции останется неизменным, а осевые моменты будут изменяться, при этом их сумма останется величиной постоянной. Поскольку сумма переменных величин постоянна, то одна из них уменьшается, а другая увеличивается, и наоборот. Момент инерции относительно какой-либо оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.
4. Что такое главные центральные оси инерции?

Оси, относительно которых центробежный момент инерции равен нулю, называют главными осями (иногда их называют главными осями инерции).
5. Какая связь существует между моментами инерции относительно параллельных осей, из которых одна является центральной?

Момент инерции относительно любой оси равен моменту инерции
относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.

Момент инерции относительно центральной оси меньше, чем момент инерции относительно любой нецентральной оси сечения, параллельной центральной.
6. Напишите формулы для вычисления осевых моментов инерции для прямоугольника, равнобедренного треугольника, круга и кольца?

Для прямоугольника размером b × h:Ix = bh3 /12

Для квадрата со стороной а:Ix = a4 / 12

Для круга диаметром d:Ix = Iy ≈ 0,05 d4

Для кольцевого сечения размером D × d:Ix = Iy ≈ 0,05 (D4 - d4)
7. Как определяют осевые моменты инерции сложных составных сечений?

К сложным сечениям относят сечения, состоящие из нескольких простых фигур. Для определения геометрических характеристик составных сечений используется. Сечение разбивают на несколько простых фигур, моменты инерции которых известны. В центре тяжести каждой фигуры назначают локальную систему координат. Выбирают систему координат относительно которой будет производиться расчет. Затем все геометрические характеристики отдельных частей суммируются, а геометрические характеристики отверстий вычитаются.

Тема 2.5. Изгиб.
1. В каком случае балка работает на изгиб?

Если силы, действующие на стержень, перпендикулярны его оси, то стержень изгибается, или, говорят, работает на изгиб.

Балка - это призматический стержень с прямолинейной осью, работающий на изгиб. Изгиб - это вид деформации, при котором первоначально прямолинейная ось стержня искривляется.
2. Что такое чистый и поперечный изгиб? Какие внутренние силовые факторы возникают в поперечных сечениях бруса в этих случаях?

Чистым называется изгиб, при котором изгибающий момент является единственным внутренним силовым фактором, возникающем в поперечном сечении балки. В поперечном сечении стержня наряду с изгибающим моментом возникает также и поперечная сила. Такой изгиб называют поперечным.
3. Каким методом определяют внутренние силовые факторы, действующие в поперечных сечениях на изгиб?

Методом сечений.
4. Чему равна поперечная сила и изгибающий момент в произвольном сечении балки при изгибе?

В поперечном сечении балки возникает только изгибающий момент, постоянный по величине. При поперечном изгибе в сечении возникает изгибающий момент и поперечная сила. Изгибающий момент в произвольном сечении балки численно равен алгебраической сумме моментов всех внешних сил, приложенных к отсеченной части, относительно рассматриваемого сечения.
5. Для чего строятся эпюры поперечных сил и изгибающих моментов?

Для того, чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента М и положение сечения, в котором он возникает. Точно также, надо знать и наибольшую поперечную силу Q. Для этой цели строят эпюры изгибающих моментов и поперечных сил. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы.
6. Сформулируйте правило знаков для поперечной силы и изгибающего момента?

Изгибающий момент считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз. Таким образом, условливаясь откладывать положительные ординаты эпюры М вверх от оси, мы получаем, что эпюра оказывается построенной со стороны сжатых волокон балки.
7. Как меняется характер эпюр поперечных сил и изгибающих моментов в точках приложения сосредоточенных, сил и моментов?

На эпюре изгибающих моментов видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой q эпюра изгибающих моментов изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке.
8. Напишите формулы для определения осевых моментов сопротивления при изгибе для прямоугольника, круга и кольца?

формула осевого момент сопротивления при изгибе для прямоугольного поперечного сечения: ;

формула осевого момент сопротивления при изгибе для круглого поперечного сечения: .

формула осевого момент сопротивления при изгибе для кольца:

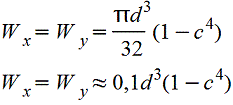
9. Изгиб прямого бруса?

Изгибом называется такой вид деформации, когда под действием внешних сил в поперечных сечениях стержня (бруса) возникают изгибающие моменты. В ряде случаев одновременно с изгибающими моментами в поперечных сечениях возникают поперечные (перерезывающие) силы.

Тема 2.6. Сдвиг и кручение.
1. В чем состоит деформация сдвига?

Если рассматривать параллелепипед, то длины ребер его не изменяются, лишь углы между боковыми гранями, каждая грань при деформации частично сдвига перемещается относительно противоположной грани.
2. Что такое модуль сдвига и как он связан с модулем продольной упругости?

Модулем сдвига (модуль упругости II рода, модуль упругости при сдвиге) – называется физическая величина, характеризующая упругие свойства материалов и их способность сопротивляться сдвигающим деформациям. Обозначается латинской буквой G, единица измерения – Паскаль [Па].
3. Как определяется крутящий момент в произвольном сечении?

Крутящий момент в любом сечении вала определяют методом сечений через внешние крутящие моменты. Крутящий момент Т в произвольном поперечном сечении вала численно равен сумме внешних моментов, приложенных по одну сторону от рассматриваемого поперечного сечения.

Т=ΣM_z_.
4. Какая зависимость существует между передаваемой валом мощностью, вращающим моментом и угловой скоростью?

Зависимость между передаваемой мощностью P в кВт, угловой скоростью ω,

С^-1 и выраженным внешним моментом Мвр в Н×М, скручивающим вал, запишется в таком виде: Мвр=10³*Р/ω.

5. На каких гипотезах и допущениях основаны выводы формул для определения касательных напряжений и углов поворота сечений при кручении бруса круглого сечения?

1.Поперечные сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к ней и после деформации (гипотеза плоских сечений); они лишь поворачиваются на некоторые углы вокруг этой оси.

2. Радиусы поперечных сечений не искривляются и сохраняют свою длину.

3. Расстояние (вдоль оси бруса) между поперечными сечениями не изменяется.

Формулы, выведенные на основании этих положений, совпадают с формулами, полученными точными методами теории упругости, и подтверждаются экспериментально.
6. Каков закон изменения касательных напряжений по площади поперечного сечения при кручении?

Формулировка закона Гука при кручении: касательные напряжения в произвольной точке поперечного сечения вала, отстоящей от центра тяжести на расстоянии 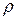, пропорциональны относительному углу закручивания. В точках, равноудаленных от центра тяжести сечения, численные значения касательных напряжений одинаковы.

Из формулы закона Гука при кручении следует: касательные напряжения в поперечном сечении вала изменяются по линейному закону (пропорционально расстоянию от точки до центра тяжести). Касательные напряжения равны нулю в центре вала и достигают максимального значения (τ_max ) в точках контура поперечного сечения.
7. Что является геометрическими характеристиками сечения вала при кручении?

Геометрическими характеристиками прочности и жесткости сечения являются соответственно полярный момент сопротивления и полярный момент инерции, значения которых зависят не только от площади, но и от формы сечения. Рациональным (т.е. дающим экономию материала) является кольцевое сечение, имеющее по сравнению с круглым сплошным меньшую площадь при равном моменте сопротивления (моменте инерции).
8. Почему выгоднее применять валы кольцевого, а не сплошного сечения?

В сплошном валу материал, находящийся в центральной части в значительной степени недогружен, его вклад в прочность вала мал. Поэтому рациональным для валов считается кольцевое сечение.

Тема 2.7. Изгиб и кручение. Гипотезы прочности.
1. Почему в случае одновременного действия изгиба и кручения оценку прочности производят, применяя гипотезы прочности?

Гипотезы прочности – это научные предположения об основной причине достижения материалом предельного напряженного состояния при сочетании основных деформаций.

В настоящее время при вычислении эквивалентных напряжений используют три гипотезы прочности: гипотезу наибольших касательных напряжений (или третья гипотеза прочности), гипотезу Мора (четвертая гипотеза прочности) и энергетическую гипотезу (пятая гипотеза прочности).
2. Приведите примеры деталей, работающих на изгиб с кручением?

Мачта, находящаяся под воздействием поперечной внешней силы, приложенной на некотором расстоянии от оси элемента. Балка с односторонне загруженной плитой.
3. Какие точки поперечного сечения являются опасными, если брус круглого поперечного сечения работает на изгиб с кручением?

Опасными являются две точки поперечного сечения , расположенные на пересечении плоскости действия изгибающего момента с контуром поперечного сечения.

Тема 2.8. Устойчивость центрально-сжатых стержней.
1. На примере сжатого стержня объясните явление потери устойчивости?

Обычно потеря устойчивости системы сопровождается большими перемещениями, возникновением пластических деформаций или разрушением. Возможны также случаи, когда система, потеряв устойчивость, переходит в режим незатухающих колебаний. Особая опасность потери устойчивости заключается в том, что она происходит внезапно и при низких значениях напряжений, когда прочность материала еще далеко не исчерпана.

2. Что такое критическая сила?

Критическая сила - наименьшая продольная сила, при которой возможны как прямолинейная, так и криволинейная форма равновесия первоначально прямолинейного бруса.
3. Что такое гибкость стержня и предельная гибкость материала? От каких факторов они зависят?

Гибкость стержня — отношение расчетной длины стержня к наименьшему радиусу инерции его поперечного сечения.

Это выражение играет важную роль при проверке сжатых стержней на устойчивость. В частности, от гибкости зависит коэффициент продольного изгиба .

Величина λпред зависит только от вида материала:

4. Какое сечение стержня (сплошное или кольцевое) более рационально с точки зрения устойчивости и почему?

С этой точки зрения более рационально кольцевое сечение по сравнению со сплошным круглым сечением, так как на поверхности стержня возникает максимальное напряжение.

Детали машин.

Дата добавления: 2019-07-17; просмотров: 836; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!