Тема 1.6. Центр тяжести тела.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ КОМИ

КОМИ РЕСПУБЛИКАСА ЙÖЗÖС ВЕЛÖДАН МИНИСТЕРСТВО

Государственное профессиональное образовательное учреждение

«Сыктывкарский автомеханический техникум»

«СЫКТЫВКАРСА АВТОМЕХАНИЧЕСКӦЙ ТЕХНИКУМ»

УДЖСИКАСӦ ВЕЛӦДАН КАНМУ УЧРЕЖДЕНИЕ

Рассмотрено и принято на заседании предметно-цикловой комиссии______________20___г. протокол №______ Председатель ПЦК ____________

Утверждаю: Зам. директора ГПОУ «САТ» _______

Рабочая тетрадь

По дисциплине

«Техническая механика»

Специальность 23.02.03

Группа ТОЗ -11

ФИО студента Булыгин Андрей Николаевич

Сыктывкар

2019

Содержание.

Раздел I Статика.

Тема 1.1. Основные понятия статики.

Тема 1.2. Плоская система сходящихся сил.
Тема 1.3. Пара сил.
Тема 1.4. Плоская система произвольно расположенных сил

Тема 1.5. Пространственная система сил.

Тема 1.6. Центр тяжести тела
Тема 1.7. Кинематика точки

Тема 1.8. Простейшие движения твердого тела

Тема 1.9. Основные понятия и аксиомы динамики

Тема 1.10. Работа и мощность

Раздел 2. Основы сопротивления материалов
Тема 2.1. Основные положения
Тема 2.2. Растяжение и сжатие
Тема 2.5. Изгиб
Тема 2.6. Сдвиг и кручение
Тема 2.7. Изгиб и кручение. Гипотезы прочности

Тема 2.8. Устойчивость центрально-сжатых стержней

Раздел 3. Детали машин.

Тема урока №1: «Цели и задачи курса. Основные требования, предъявляемые к узлам и деталям. Основные критерии работоспособности деталей машин».

Тема урока №2: «Назначение и классификация передач. Кинематические и силовые соотношения в передачах».

Тема урока №3: «Фрикционные передачи».

Тема урока № 4 «Общие сведения и классификация зубчатых передач. Основы теории зацепления».

Тема урока №5 «Зацепление 2-ух эвольвентных зубчатых колёс. Краткие сведения о методах изготовления зубчатых колёс, их конструкциях, материалах».

Тема урока №6 «Зацепление зубчатого колеса с рейкой. Виды разрушения зубчатых колёс».

Тема урока №7 « Прямозубые цилиндрические передачи».

Тема урока №8 «Косозубые цилиндрические передачи и конические передачи».

Тема урока № 9 «Передача винт-гайка».

Тема урока №10 «Червячные передачи».

Тема урока №11 «Общие сведения о редукторах».

Тема урока №12 «Ремённые передачи».

Тема урока №13 «Цепные передачи».

Тема урока № 14 «Валы и оси».

Тема урока №15 « Подшипники скольжения».

Тема урока №16 «Подшипники качения».

Тема урока № 17 «Муфты».

Раздел I

Статика.

Тема 1.1.Основные понятия статики.

1. Назовите разделы теоретической механики и укажите, какие вопросы в них изучают?

1) Кинематика – изучение движения тел без учёта сил.

2) Статика – изучение неподвижности тел.

3) Динамика – изучение движения тел под действием сил.

2. Дайте определение материи. Перечислите формы движения материи?

Материя - общий термин, определяющийся множеством всего содержимого пространства-времени и влияющее на его свойства.
Формы движения: Механическое движение (поступательное, вращательное), физическое движение, химическое движение.

- Органическое или биологическое – развитием белковой формы жизни.

- Социальное движение – все изменения в обществе.

Эта классификация к настоящему времени устарела. В частности, сейчас неправомерно физическое движение сводить только к тепловому. Поэтому современная классификация форм движения материи включает:

- пространственное перемещение (квантово-механическое);

- электромагнитное движение, определяемое как взаимодействие заряженных частиц;

- гравитационную форму движения; сильное (ядерное) взаимодействие;

- слабое взаимодействие (поглощение и излучение нейтрона);

- химическую форму движения (процесс и результат взаимодействия молекул и атомов);

- геологическую форму движения материи (связанную с изменением в геосистемах - материках, слоях земной коры и т. д.);

- космическая форма движения, изучаемая астрофизикой;

3. В чем общность понятий абсолютно твердого тела и материальной точки и в чем их различие?

Материальная точка, в отличие от абсолютно твёрдого тела, не обладает объёмом, т.е. не заполняет область пространства, но движение материальной точки и абсолютно твёрдого тела можно изучать только относительно других тел, при этом в механике оно определяется с помощью выбранной системы координат.

4. Дайте определение силы?

Сила - физическая векторная величина, являющаяся мерой воздействия на данное тело со стороны других тел или полей.

5. Какие системы сил называют статически эквивалентными?

Системой сил, эквивалентной нулю (или равновесной системой сил), называют такую систему сил, действие которой на твердое тело или материальную точку, находящиеся в покое или движущиеся по инерции, не приводит к изменению состояния покоя или движения по инерции этого тела или материальной точки.

6. Что такое равнодействующая система сил, уравновешивающая сила?

Равнодействующей системой сил называют силу, действие которой заменяет собой действие данной системы сил. Силу, образующую с равнодействующей уравновешенную систему сил, называют уравновешивающей силой.

7. Сформулируйте аксиомы статики?

1) Не нарушая механического состояния тела, к нему можно приложить или отбросить уравновешенную систему сил.

2) О действии и противодействии. При всяком действии одного тела на другое со стороны другого тела имеется противодействие, такое же по величине, но противоположное по направлению.

3) О двух силах. Две силы, приложенные к одному и тому же телу, взаимно уравновешены (их действие эквивалентно нулю) тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны.

4) О равнодействующей. Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и равна диагонали параллелограмма, построенного на этих силах как сторонах.

5) Аксиома затвердевания. Если деформируемое тело находилось в равновесии, то оно будет находиться в равновесии и после его затвердевания.

6) Аксиома о связях. Механическое состояние системы не изменится, если освободить её от связей и приложить к точкам системы силы, равные действовавшим на них силам реакций связей.

8. Какие тела называются свободными, а какие несвободными?

Тело называется свободным, если его перемещения в пространстве с течением времени ничем не ограничены.

В любом другом случае тело является несвободным.

9. Что называется связью?

Связи – ограничения, налагаемые на свободу любого несвободного тела.

10. Что такое реакция связи?

Силы, с которыми связи действуют на данное тело, называются реакциями связей.

11. Перечислите виды связей и укажите направление соответствующих им реакций?

Виды связей:

· Гладкая поверхность (опора без трения)

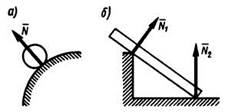
· Шероховатая поверхность

· Цилиндрический шарнир (подшипник)

· Сферический шарнир

· Гибкая нить

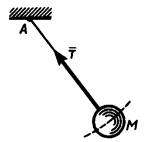
· Невесомый стержень

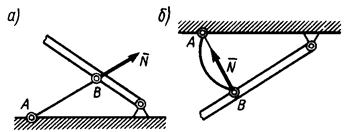
· Жесткая заделка (защемление)

· Опорные реакции балок

· Шарнирно-подвижная опора

· Шарнирно-неподвижная опора

Тема 1.2. Плоская система сходящихся сил.

1. Геометрический способ нахождения равнодействующей плоской системы сходящихся сил.

Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у

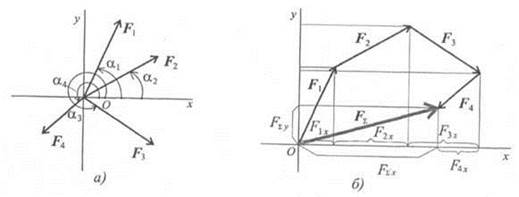
FΣx = Flx + F2x + F3x + F4x; FΣy = Fly + F2y + F3y + F4y;

; .

Модуль (величину) равнодействующей можно найти по известным проекциям:

Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат Растяжение сжатие Продольные силы и определение напряжений.

;

Рис.3.5

2. Что называется проекцией силы на ось? В каком случае проекция силы на ось равна О?

Проекция силы на ось – это алгебраическая величина, равная произведению модуля силы на косинус угла между положительным направлением оси и вектором силы (т.е. это отрезок, откладываемый силой на соответствующие оси). Проекция силы равна нулю, если сила перпендикулярна выбранной оси проекции.
3. Как найти силовое значение и направление равнодействующей системы сил, если заданы проекции составляющих сил на две взаимноперпендикулярные оси?

Проекция вектора силы на ось равна произведению вектора на косинус прилежащего к оси угла. Поэтому сила равна частному от деления проекции силы на ось на косинус прилежащего к оси узла. Если численное значение проекции положительно, то направление вектора силы совпадает с направление оси, в противоположном случае – не совпадает.
4. Сформулируйте аналитическое условие равновесия плоской системы сходящихся сил.

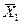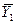Пусть { , , , … } система сходящихся сил на плоскости имеет равнодействующую . Обозначим через и проекции этой равнодействующей на оси системы координат XOY, а через , ; , ; ... , ; проекции сил , , , … на те же оси. Из математики известно, что проекция суммы векторов на какую – либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. Тогда:

Модуль равнодействующей равен:

Аналитически равнодействующая системы сходящихся сил определяется формулой

5. Определение равнодействующей аналитическим способом

Для заданной системы сходящихся сил определить проекции равнодействующей на оси Х и У: F_Σх и F_Σу.

Определяем проекции всех сил системы на ось Х:

F_1х= F₁*cos45= 20*0,707107=14,14214 кН

F_2х= F₂*cos0= 30*1=30 кН

F_3х= - F₃*cos60= -42*0,5= - 21 кН

Определяем проекцию равнодействующей на ось Х:

F_Σх = F_1х+ F_2х+ F_3х= 14,14214+30-21=23,14214 кН

Определяем проекции всех сил системы на ось Y:

F_1y= F₁*cos45= 20*0,707107=14,14214 кН

F_2y= F₂*cos90= 30*0=0 кН

F_3y= - F₃*cos30= -42*0,866025= - 36.37305 кН

Определяем проекцию равнодействующей на ось Y:

F_Σy = F_1y+ F_2y+ F_3y= 14,14214+0-36,37305= -22,23091 кН.

Тема 1.3. Пара сил.
1. Что такое пара сил?

Парой сил называются две равные и параллельные силы, не лежащие на одной прямой и направленные в противоположные стороны.
2. Что такое момент пары сил, плечо пары сил?

Пара сил оказывает вращающее действие, которое может быть оценено моментом пары.

Моментом пары называется вектор с такими признаками:

§ он перпендикулярен плоскости пары;

§ направлен в ту сторону, откуда вращение, которое осуществляет пара, видно против часовой стрелки;

§ его модуль равняется произведению модуля одной из сил пары на плечо пары с учетом знака

M(F₁,F₂ ) = F₁h = F₂h

где h – плечо пары - расстояние между линиями действия сил пары, т.е. длина перпендикуляра, проведенного из произвольной точки линии действия одной из сил пары на линию действия второй силы.

Момент пары считается положительным, если силы пары стремятся повернуть плоскость, в которой они расположены, против хода часовой стрелки

Момент пары сил может быть определен как векторная величина:

M(F₁,F₂ ) = AB ⊗ F₂ = BA ⊗ F₁

т.е. вектор M(F₁,F₂ ) всегда перпендикулярен плоскости, в которой расположена пара сил, и его направление определяется правилом векторного произведения

Поскольку действие пары сил оценивается величиной и направлением вращающего момента, то на плоскости пару сил изображают в любом месте твердого тела, задавая величину и направление вращающего действия.
3. Сформулируйте условие равновесия системы пар сил.

Если на твердое тело действует несколько пар сил, как угодно расположенных в пространстве, то последовательно применяя правило параллелограмма к каждым двум моментам пар сил, можно любое количество пар сил заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

Тема 1.4. Плоская система произвольно расположенных сил.
1. Что такое момент силы относительно точки? Как берется знак момента силы относительно точки? Что называется плечом силы?

Моментом силы относительно точки называется векторное произведение радиус-вектора точки приложения силы на вектор силы. Плечо силы (в механике) - кратчайшее расстояние от данной точки (центра) до линии действия силы, т. е. длина перпендикуляра, опущенного из этой точки на линию действия силы. Если сила направлена против часовой стрелки, относительно точки вращения, то момент имеет положительное значение величины, если по часовой стрелке, то отрицательный.
2. В каком случае момент силы относительно точки равен нулю?

Если сила и ось лежат в одной плоскости, то момент силы относительно этой оси равен нулю, то есть если линия действия силы проходит через точку, т.к. в этом случае расстояние от точки до силы равно нулю.
3. Что такое главный вектор и главный момент плоской системы сил?

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:

R = F₁ + F₂ + ... + F_n = F_i.

Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.

Главным моментом системы сил относительно центра O называется вектор L_O, равный сумме векторных моментов этих сил относительно точки О:

L_O = M_O(F₁) + M_O(F₂) + ... + M_O(F_n) = M_O(F_i).

4. Сформулируйте теорему Вариньона?

Момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.
5. Сформулируйте аналитическое условие равновесия плоской системы произвольно расположенных сил?

Для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат x и y равнялись нулю, и чтобы алгебраическая сумма моментов этих сил относительно любой точки плоскости также равнялась нулю.

Условие равновесия упрощенно записывается в виде равенств:

ΣX = 0; ΣY = 0; ΣM = 0.

6. Укажите три вида уравнения равновесия плоской системы произвольно расположенных сил?

Математически условие равновесия пространственной системы произвольно расположенных сил можно записать в виде уравнений:

· ΣX = 0; ΣMx(Fi) = 0;

· ΣY = 0; ΣMy(Fi) = 0;

· ΣZ = 0; ΣMz(Fi) = 0.

7. Укажите, как рационально выбрать направления осей координат и центр моментов?

В качестве центра моментов рекомендуется выбрать точку, где пересекаются две неизвестные силы; уравнение моментов относительно этой точки будут содержать только одну неизвестную. Направление координат осей x и y следует выбрать так, чтобы оси были перпендикулярны некоторым неизвестным силам.

8. Какие нагрузки называются сосредоточенными и распределенными?

Сила не может быть приложена к точке, поскольку точка - безразмерная, бесконечно малая единица пространства, поэтому фактически силы воздействуют на очень малую площадку, размерами которой пренебрегают. Такие силы называют сосредоточенными. Часто встречаются силы, приложенные не к точке, а к объему или поверхности тела, например сила тяжести, давления ветра, воды и т.п., т.е. нагрузку воспринимает не бесконечно малая площадка, а значительная площадь или объем тела. Такие силы называют распределенными.

9. Что такое интенсивность равномерно распределенной нагрузки?

Распределенная нагрузка, имеющая постоянную интенсивность по всей длине участка называется равномерно распределенной. Интенсивность - нагрузка, приходящаяся на 1 метр.
10. Как найти числовое значение, направление и точку приложения равнодействующей равномерно распределенной нагрузки?

Модуль равнодействующей равномерно распределенной нагрузки равен Q = ql. Точка приложения сосредоточенной силы находится в середине отрезка приложения распределённой силы, которую заменяют. Направление сосредоточенной силы перпендикулярно отрезку приложения силы и

сонаправлено с направлением распределённой нагрузки.

11. Какие системы называются статически определимыми?

Статически определимой системой понимается такая система, для которой усилия во всех ее элементах могут быть определены с применением лишь уравнений равновесия.
12. Что называется силой трения?

Силами трения называют силы, возникающие при соприкосновении поверхностей двух тел или частей одного тела и препятствующие их взаимному перемещению. Они приложены к телам (или к их частям) вдоль поверхности соприкосновения и всегда направлены в сторону, противоположную относительной скорости движения.
13. Перечислите основные законы трения - скольжения?

Закон Кулона.

Сила трения не зависит от величины площади трущихся поверхностей. Первый закон можно объяснить с помощью следующих умозаключений. Если площадь трущихся поверхностей увеличится, то увеличится и количество сцепляющихся неровностей, но уменьшится давление на опорную поверхность, которое обратно пропорционально площади контакта тел. Поэтому сопротивление относительному перемещению останется прежним.

Закон Кулона.

Максимальная сила трения прямо пропорциональна нормальной составляющей внешних сил, действующих на поверхности тела. Второй закон Кулона говорит о том, что если увеличится нормальная составляющая внешних сил, действующих на поверхности тела (иначе говоря, увеличится сила нормального давления или реакции), то во столько же раз возрастет максимальная сила трения.

Закон Кулона.

Сила трения зависит от материала тел, состояния трущихся поверхностей и рода смазки. Согласно третьему закону трения скольжения, коэффициент трения скольжения зависит от материалов трущихся тел, качества обработки их поверхности (степени шероховатости), рода и температуры смазки. В зависимости от наличия между сопрягаемыми поверхностями слоя смазки трение подразделяется на два вида: трение без смазочного материала (сухое трение) и трение в условиях смазки

14. Что такое угол трения, конус трения?

Рассмотрим твердое тело на шероховатой поверхности, находящееся под действием активных сил в предельном состоянии равновесия, т.е. когда сила трения достигает своего наибольшего значения при данном значении нормальной реакции.

В этом случае полная реакция шероховатой поверхности отклонена от нормали к общей касательной плоскости трущихся поверхностей на наибольший угол (R^max). Этот наибольший угол между полной реакцией, построенной на наибольшей силе трения при данной нормальной реакции и направлением нормальной реакции, называется углом трения φ:

tgφ = F_тр^max/N = fN/N = f.

Конус трения – поверхность, образованная линией действия максимальной реакции опорной поверхности при движении тела в различных направлениях.

15. Каковы особенности трения качения?

В большинстве случаев величина трения качения гораздо меньше величины трения скольжения при прочих равных условиях, и потому качение является распространенным видом движения в технике. Трение качения возникает на границе двух тел, и поэтому оно классифицируется как вид внешнего трения.

Тема 1.5. Пространственная система сил.
1. Напишите уравнения равновесия для пространственной системы сходящихся сил?

Равнодействующая R пространственной системы сходящихся сил приложена в точке пересечения линий действия слагаемых сил и является замыкающей стороной силового многоугольника, построенного на этих силах, т. е.

R= Σ Fk

В отличие от соответствующей плоской задачи силовой многоугольник не является плоским, т.е. он представляет собой ломаную пространственную линию. Проекции равнодействующей силы R на оси декартовых координат х, у, z равны суммам проекций слагаемых сил па соответствующие оси, т. е.

Rx= Σ Fkx , Ry= Σ Fky , Rz= Σ Fkz

Модуль равнодействующей R равен

направляющие косинусы даются формулами:

cos(R,^ i) = Rx / R , cos(R,^ j) = Ry / R , cos(R,^ k) = Rz / R

Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая равнялась нулю: R=0, т. е. чтобы силовой многоугольник был замкнут. При этом уравнения равновесия имеют вид

Σ Fkx =0, Σ Fky =0 , Σ Fkz =0

2. Что такое момент силы относительно оси? В каких случаях момент силы относительно оси равен нулю?

Для характеристики вращательного действия силы на тело, закрепленное на оси, служит момент относительно оси – алгебраический момент проекции этой силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с этой плоскостью. Момент считается положительным, если проекция силы на плоскость, перпендикулярную к оси, стремится вращать тело вокруг положительного направления оси против движения часовой стрелки, и отрицательным, если она стремится вращать тело по движению часовой стрелки:

M_z (F) = M_o(F _П ) = ±hF _П,

где F_П – вектор проекции силы F на плоскость П, перпендикулярную к оси Oz, точка O – точка пересечения оси Ozс плоскостью П.

Свойства момента относительно оси:

1) момент равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси;

2) момент равен нулю, если линия действия силы пересекается с осью. В этом случае равно нулю плечо силы.

Другими словами, момент относительно оси равен нулю, если сила и ось лежат в одной плоскости.

3. Напишите уравнения равновесия для произвольной пространственной системы сил?

Равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.

∑x_i =0, ∑M_ix=0; ∑y_{i =0}, ∑M_iy=0; ∑z_i =0, ∑M_iz=0.

Тема 1.6. Центр тяжести тела.

1. Что такое центр параллельных сил?

Центр параллельных сил есть точка, через которую проходит линия равнодействующей системы параллельных сил, приложенных в заданных точках, при любом изменении направления этих сил в пространстве.

2. Как найти координаты центра параллельных сил?

Для определения координат центра параллельных сил воспользуемся теоремой Вариньона.

Относительно оси x

Mx(R) = ΣMx(Fk), -yCR = ΣykFk и yC = ΣykFk /ΣFk.

Относительно оси y

My(R) = ΣMy(Fk), -xCR = ΣxkFk и xC = ΣxkFk /ΣFk.

Чтобы определить координату zC, повернем все силы на 90° так, чтобы они стали параллельны оси y. Тогда

Mz(R) = ΣMz(Fk), -zCR = ΣzkFk и zC = ΣzkFk /ΣFk.

Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид

rC =ΣrkFk /ΣFk.

3. Что такое центр тяжести тела?

Центр тяжести тела - неизменно связанная с твердым телом точка, через которую проходит равнодействующая сил тяжести, действующих на частицы этого тела при любом положении тела в пространстве. У однородного тела, имеющего центр симметрии (круг, шар, куб и т. д.), центр тяжести находится в центре симметрии тела. Положение центра тяжести твердого тела совпадает с положением его центра масс.

4. Как найти центр тяжести прямоугольника, треугольника, круга?

Для нахождения центра тяжести треугольника, необходимо нарисовать треугольник – фигуру, состоящую из трех отрезков, соединенных между собой в трех точках. Перед тем, как найти центр тяжести фигуры, необходимо, используя линейку, измерить длину одной стороны треугольника. В середине стороны поставьте отметку, после чего противоположную вершину и середину отрезка соедините линией, которая называется медианой. Тот же самый алгоритм повторите со второй стороной треугольника, а затем и с третьей. Результатом вашей работы станут три медианы, которые пересекаются в одной точке, которая будет являться центром тяжести треугольника. Если необходимо определить центр тяжести круглого диска однородной структуры, то для начала найдите точку пересечения диаметров круга. Она и будет центром тяжести данного тела. Центр тяжести шара - геометрический центр сферы.

5. Как найти координаты центра тяжести плоского составного сечения?

Метод разбиения: если плоскую фигуру можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всей фигуры опредляются по формулам:

ХC = ( sk xk ) / S; YC = ( sk yk ) / S,

где xk, yk - координаты центров тяжести частей фигуры;

sk - их площади;

S = sk - площадь всей фигуры.

6. Центр тяжести

1. В каком случае для определения центра тяжести достаточно определить одну координату расчетным путем?

В первом случае для определения центра тяжести достаточно определить одну координату Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.) можно представить в виде двух плоских фигур с площадями S1 и S2(S = S1 + S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны

Так как центры фигур лежат на оси ординат (х = 0), то находим только координату Ус.

2. Как учитывается площадь отверстия в фигуре 4 в формуле для определения центра тяжести фигуры?

Метод отрицательных масс

Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.

Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.

Тема 1.7. Кинематика точки.

1. В чем заключается относительность понятий покоя и движения?

Механическое движение - это изменение движения тела, или (его частей) в пространстве относительно др. тел с течением времени.

2. Дайте определение основных понятий кинематики: траектории, расстоянию, пути, скорости, ускорению, времени.

Время - это непрерывная величина, априорная характеристика мира, ничем не определяемая. В качестве основы измерения используется некая, обычно периодическая, последовательность событий, которая признаётся эталоном некоторого промежутка времени.

Скорость – это кинематическая мера движения точки, характеризующая быстроту изменения ее положения в пространстве. Скорость является векторной величиной, т. е. она характеризуется не только модулем (скалярной составляющей), но и направлением в пространстве.

Как известно из физики, при равномерном движении скорость может быть определена длиной пути, пройденного за единицу времени: v = s/t = const (предполагается, что начало отсчета пути и времени совпадают). При прямолинейном движении скорость постоянна и по модулю, и по направлению, а ее вектор совпадает с траекторией. Ускорение есть кинематическая мера изменения скорости точки во времени. Другими словами - ускорение - это скорость изменения скорости.
Как и скорость, ускорение является величиной векторной, т. е. характеризуется не только модулем, но и направлением в пространстве.

При прямолинейном движении вектор скорости всегда совпадает с траекторией и поэтому вектор изменения скорости тоже совпадает с траекторией.

Из курса физики известно, что ускорение представляет собой изменение скорости в единицу времени. Если за небольшой промежуток времени Δt скорость точки изменилась на Δv, то среднее ускорение за данный промежуток времени составило: аср = Δv/Δt.

Среднее ускорение не дает представление об истинной величине изменения скорости в каждый момент времени. При этом очевидно, что чем меньше рассматриваемый промежуток времени, во время которого произошло изменение скорости, тем ближе значение ускорения будет к истинному (мгновенному).
Отсюда определение: истинное (мгновенное) ускорение есть предел, к которому стремится среднее ускорение при Δt, стремящемся к нулю:

а = lim аср при t→0 или lim Δv/Δt = dv/dt.

Учитывая, что v = ds/dt, получим: а = dv/dt = d2s/dt2.

Истинное ускорение в прямолинейном движении равно первой производной скорости или второй производной координаты (расстояния от начала отсчета перемещения) по времени. Единица ускорения - метр, деленный на секунду в квадрате (м/с2).

Траектория — линия в пространстве, вдоль которой движется материальная точка.
Путь — это длина траектории. Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.

Расстояние определяет положение точки на ее траектории и отсчитывается от некоторого начала отсчета. Расстояние является алгебраической величиной, так как в зависимости от положения точки относительно начала отсчета и от принятого направления оси расстояний оно может быть и положительным, и отрицательным. В отличие от расстояния путь, пройденный точкой, всегда определяется положительным числом. Путь совпадает с абсолютным значением расстояния только в том случае, когда движение точки начинается от начала отсчета и совершается по траектории в одном направлении.

3. Какими способами может быть задан закон движения точки?

1.Естественный способ задания движения точки.

При естественном способе задания движения предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении. Чтобы задать закон движения точки естественным способом необходимо:

1) знать траекторию движения;

2) установить начало отсчета на этой кривой;

3) установить положительное направление движения;

4) дать закон движения точки по этой кривой, т.е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t) .

2.Векторный способ задания движения точки.

В этом случае положение точки на плоскости или в пространстве определяется вектором-функцией. Этот вектор откладывается от неподвижной точки, выбранной за начало отсчета, его конец определяет положение движущейся точки.

3.Координатный способ задания движения точки

В выбранной системе координат задаются координаты движущейся точки как функции от времени. В прямоугольной декартовой системе координат это будут уравнения:

x=x(t); y=y(t); z=z(t).
4. Как направлен вектор истинной скорости точки при криволинейном движении?

Истинная (мгновенная) скорость есть предел, к которому стремится средняя скорость при Δt, стремящемся к нулю:

v = lim v_ср при t→0 или v = lim (Δs/Δt) = ds/dt.

Таким образом, числовое значение истинной скорости равно v = ds/dt.
Истинная (мгновенная) скорость при любом движении точки равна первой производной координаты (т. е. расстояния от начала отсчета перемещения) по времени.

При Δt стремящемся к нулю, Δs тоже стремится к нулю, и, как мы уже выяснили, вектор скорости будет направлен по касательной (т. е. совпадает с вектором истинной скорости v). Из этого следует, что предел вектора условной скорости v_п, равный пределу отношения вектора перемещения точки к бесконечно малому промежутку времени, равен вектору истинной скорости точки.
5. Как направлены касательное и нормальное ускорения точки?

Направление вектора ускорения совпадает с направлением изменения скорости

Δ = - ₀

Касательное ускорение в данной точке направлено по касательной к траектории движения точки; если движение ускоренное, то направление вектора касательного ускорения совпадает с направлением вектора скорости; если движение замедленное – то направление вектора касательного ускорения противоположно направлению вектора скорости. Нормальное ускорение направлено по нормали (перпендикуляру) к мгновенному вектору направления движения и характеризуется радиусом кривизны движения (r).

6. Какое движение совершает точка, если касательное ускорение равно нулю, а нормальное не изменяется с течением времени?

Равномерное криволинейное движение характеризуется тем, что численное значение скорости постоянно (v = const), скорость меняется лишь по направлению. В этом случае касательное ускорение равно нулю, так как v = const,

а нормальное ускорение не равно нулю, так как r — конечная величина.

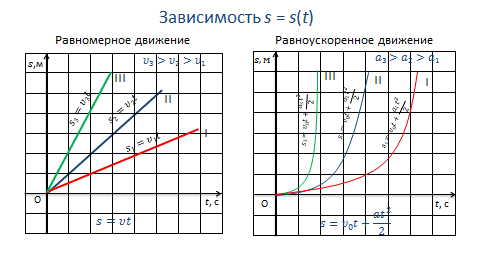
7. Как выглядят кинематические графики при равномерном и равнопеременном движении?

При равномерном движении тело за любые равные промежутки времени проходит равные пути. Для кинематического описания равномерного прямолинейного движения координатную ось OX удобно расположить по линии движения. Положение тела при равномерном движении определяется заданием одной координаты x. Вектор перемещения и вектор скорости всегда направлены параллельно координатной оси OX. Поэтому перемещение и скорость при прямолинейном движении можно спроецировать на ось OX и рассматривать их проекции как алгебраические величины.

При равномерном движении путь изменяется, согласно линейной зависимости . В координатах . Графиком является наклонная линия.

Тема 1.8. Простейшие движения твердого тела.
1. Какое движение твердого тела называется поступательным?

Поступательным движением твердого тела называется такое его движение, при котором любая прямая, проведенная в теле, остается параллельной своему первоначальному положению во все время движения.

2. Перечислите свойства поступательного движения твердого тела?

Свойства поступательного движения определяются следующей теоремой: при поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.

3. Дайте определение вращательного движения твердого тела вокруг неподвижной оси?

Движение, при котором по крайней мере две точки твердого тела или неизменяемой системы остаются неподвижными, называется вращательным; прямая линия, соединяющая эти две точки, называется осью вращения.
4. Как записывается в общем виде уравнение вращательного движения твердого тела?

φ=φ(t) – уравнение вращательного движения твердого тела.
5. Напишите формулу, устанавливающую связь между частотой вращения тела п и угловой скоростью вращения?

ω – угловая скорость; ν – частота вращения; φ – угол поворота.
6. Дайте определение равномерного и равнопеременного вращательного движения?

Равнопеременное движение — это движение с постоянным касательным ускорением:

at = const.

Если угловое ускорение все время остается постоянным, то такое вращение называется равнопеременным.
7. Какая дифференциальная зависимость существует между угловым перемещением, угловой скоростью и угловым ускорением?

φ – угловое перемещение; ω – угловая скорость; ε – угловое ускорение.

8. Какая зависимость существует между линейным перемещением, скоростью и ускорением точек вращающегося тела и угловым перемещением, скоростью и ускорением тела?

S(t)=Rφ(t) S – линейное перемещение; R – радиус окружности, описываемой при вращательном движении тела; φ – угол поворота.

V = 2 * π * R * ω, где
V - линейная скорость;
R - радиус окружности;
ω - угловая скорость.

Следовательно, линейная скорость любой точки вращающегося тела равна произведению угловой скорости на расстояние от данной точки до оси вращения. Направлена эта скорость всегда по касательной к окружности, которую описывает данная точка при своем движении. Так как точки тела совершают криволинейное движение (траектории точек - окружности), то полное ускорение слагается из нормального и касательного ускорений , которые определяются ,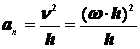

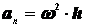
Таким образом полное ускорение точки будет Из формул следует, что полное ускорение точки вращающегося тела пропорционально ее расстоянию до оси вращения.

При вращательном движении тела вокруг оси нормальное ускорение 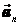называют еще центростремительным (вектор направлен по радиусу к центру кривизны), касательное ускорение называют и иначе – вращательным ускорением 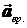(вектор ускорения направлен по касательной).

Понятие	Основные параметры	Поступательные движения	Вращательное движение
Кинематика	Расстояние	S=s(t)	φ=φ(t)
	Скорость
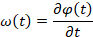
	Ускорение
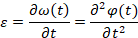
	Силовое воздействие	F=ma	M=F˟r
	Сила инертности тела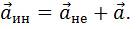
Динамика	Основной закон динамики		M=I*ε
	Работа	A=F˟S
	Мощность		N=Mω
	Кинематическая энергия	E=mV²/2+hgm

Тема 1.9. Основные понятия и аксиомы динамики.

1. Сформулируйте первую аксиому динамики (принцип инерции) и вторую аксиому динамики (основной закон динамики точки)?

Первый закон Ньютона (первый закон динамики)

Первый закон динамики, называемый аксиомой инерции, формулируется в применении к материальной точке так: изолированная материальная точка либо находится в покое, либо движется прямолинейно и равномерно.

Второй закон Ньютона (второй закон динамики)

Зависимость между силой и сообщаемым ею ускорением устанавливает второй закон Ньютона, который гласит, что ускорение, сообщаемое материальной точке силой, имеет направление силы и пропорционально ее модулю.
2. Сформулируйте две основные задачи динамики?

1) По заданному движению точки или системы определить силы, производящие это движение.

2) По заданным силам, действующим на точку или систему, определить движение этих объектов.

3. Изложите третью аксиому динамики (закон независимости действия сил) и четвертую аксиому (закон равенства действия и противодействия)?

Третья аксиома: силы взаимодействия двух материальных точек по модулю равны между собой и направлены в противоположные стороны (действие равно противодействию).

Четвертая аксиома: Если на МТ постоянной массы действует одновременно несколько сил, то каждая из этих сил действует независимо от других и сообщает МТ такое ускорение, которое она сообщила бы, действуя отдельно.

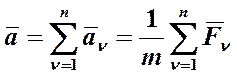
Тема 1.10. Работа и мощность.
1. Как определяется работа постоянной силы на прямолинейном пути?

A = Rs = Fs cos α,

т. е. работа силы равна произведению ее модуля на путь и на косинус угла между направлением вектора силы и направлением перемещения материальной точки.
2. Что называется мощностью?

Мощностью называется количество энергии, выделяемое или расходуемое тем или иным объектом за единицу времени.
3. Что такое механический коэффициент полезного действия?

Механическим коэффициентом полезного действия (КПД) называется абсолютная величина отношения работы сил полезного сопротивления к работе движущих сил за время установившегося движения: η= А_пс /A_дв.
4. Назовите формулу, позволяющую определить вращающийся момент через передаваемую мощность и угловую скорость вращения тела при равномерном вращении?

Если работа совершается силой, приложенной к равномерно вращающемуся телу, то мощность в этом случае может быть определена по формуле:

P = W/t = Tφ/t или P = Tω.

Следовательно, вращающий момент можно определить по формуле: T= P/ω

Раздел II

ОСНОВЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ

Тема 2.1. Основные положения.
1. Для чего изучается сопротивление материалов?

Сопротивление материалов — это наука, в которой рассматриваются основные понятия, принципы и методы инженерного расчета отдельных элементов конструкций и некоторых простейших конструкций на прочность, жесткость и устойчивость.

Несмотря на то, что конструктивные элементы машин и сооружений довольно разнообразны, при инженерном расчете их сводят к небольшому числу основных форм: стержни (прямые и кривые), пластины и оболочки, массивные тела. В основном, в курсе сопромата изучаются методы расчета прямых стержней при их растяжении, сжатии, кручении и изгибе.
2. Чем отличается упругая деформация от пластической?

В процессе деформации важное значение имеет величина межатомных связей, приложение нагрузки достаточной для их разыва приводит к необратимым последствиям (необратимая или пластическая деформация). Если нагрузка не превысила допустимых значений, то тело может вернуться в исходное состояние (упругая деформация). Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина. Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму.
3. Следует ли учитывать изменение размеров тел при составлении уравнений равновесия сил, приложенных к нему?

В сопротивлении материалов за расчетную модель принята модель идеализированного деформируемого тела и для решения поставленной задачи делается ряд допущений, одно из которых гласит:

Перемещения точек элемента (или системы элементов), обусловленные его деформацией, весьма малы по сравнению с размерами самого элемента. На основе этого допущения вводится принцип начальных размеров, согласно которому при составлении уравнений равновесия элемент или систему элементов рассматривают как недеформируемое тело. Такой подход позволяет пренебречь изменениями в расположении внешних сил при деформировании реального тела.

4. В каких случаях при действии на тело нескольких сил эффект действия каждой силы можно считать независимым от действия других сил? Какое название носит этот принцип?

Системы, для которых соблюдается условие пропорциональности между напряжениями и деформациями, подчиняются принципу суперпозиции, или принципу независимости действия сил.

В соответствии с этим принципом перемещения и внутренние силы, возникающие в упругом теле, считаются независящими от порядка приложения внешних сил. То есть, если к системе приложено несколько сил, то можно определить внутренние силы, напряжения, перемещения и деформации от каждой силы в отдельности, а затем результат действия всех сил получить как сумму действий каждой силы в отдельности. Принцип независимости действия сил является одним из основных способов при решении большинства задач механики линейных систем.

5. Какими расчетными схемами заменяются реальные объекты расчета?

Расчетная схема является схематизированным представлением реальной конструкции, в котором сознательно не учитывается ряд менее важных с точки зрения проводимого расчета факторов, относящихся к конструктивным особенностям, характеру нагружения и закрепления.

Реальный объект, освобожденный от несущественных особенностей, носит название расчетной схемы.
Реальные стержни изображаются их осями на расчетной схеме. Нагрузку, приложенную к небольшим участкам поверхности, заменяют силой, приложенной в точке, которую называют сосредоточенной и обозначают через Р. Схематизируются и свойства материала. Принято рассматривать все материалы как однородную сплошную среду.
Вводятся упрощения и в геометрию конструкции. Так, все реальные тела, один размер у которых - длина, на много больше двух других (поперечных), сводятся к схеме бруса.

Каковы геометрические признаки, присущие каждой расчетной схеме?

Геометрически изменяемая система - система, в которой возможны конечные перемещения без деформации элементов. При составлении расчетных схем в геометрию реального объекта вводятся определенные упрощения. Все тела представляются в виде бруса, оболочки или массивного тела.

называется элемент конструкции, длина которого существенно больше его поперечных размеров.

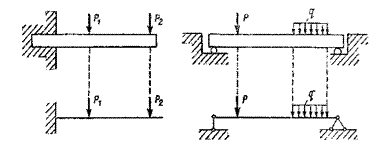
Геометрически стержень может быть образован путем перемещения плоской фигуры вдоль некоторой кривой или прямой. Эта кривая называется осью стержня, а плоская фигура, имеющая свой центр тяжести на оси и перпендикулярная к ней, называется поперечным сечением.

По форме стержни бывают:

а) прямыми;

б) кривыми (арка, крановый крюк);

в) пространственно - изогнутыми, например пружина.
6. Почему нельзя определить внутренние силовые факторы в произвольном сечении, рассматривая равновесие всего тела в целом?

Под действием нагрузки в разных элементах конструкции возникает разное внутреннее напряжение, из-за чего каждый отдельный элемент конструкции реагирует на нагрузки отлично от других.
7. В чем заключается метод сечений?

Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается и взамен ее к сечению оставшейся части прикладываются внутренние силы, действовавшие на нее до разреза со стороны отброшенной части. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием приложенных к сечению внешних и внутренних сил (третий закон Ньютона – действие равно противодействию).
Метод сечений в сопромате. При применении этого метода выгоднее отбрасывать ту часть элемента конструкции (тела), для которой проще составить уравнение равновесия. Таким образом, появляется возможность определить внутренние силовые факторы в сечении, благодаря которым оставшаяся часть тела находится в равновесии (прием, часто применяемый в Статике).
8. Можно ли с помощью метода сечений установить закон распределения внутренних силовых факторов по проведенному сечению?

Можно.

9. Что такое напряжение? Какова размерность напряжения?

Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле, под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения. Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Тема 2.2. Растяжение и сжатие.
1. В каком случае брус испытывает деформацию растяжения или сжатия?

Прямой брус испытывает деформацию центрального растяжения, сжатия, если силы или их равнодействующая действуют вдоль его оси. В этом случае в поперечном сечении бруса из шести внутренних силовых факторов отличным от нуля будет один - нормальная сила N, которая определяется методом сечений.
2. Каков закон изменения нормальных напряжений по площади поперечного сечения при растяжении и сжатии?

Чтобы понять характер напряжений и деформаций, возникающих в сжимаемом или растягиваемом брусе, представим себе прямой брус из резины, на котором нанесена сетка из продольных и поперечных линий. Если такой брус подвергнуть деформации растяжения, можно заметить, что:

· поперечные линии на брусе остаются ровными и перпендикулярными оси бруса, а расстояния между ними увеличатся;

· продольные линии останутся прямыми, а расстояния между ними уменьшатся.

Из этого эксперимента следует, что при растяжении справедлива гипотеза плоских сечений (гипотеза Бернулли), и, следовательно, все волокна бруса удлинятся на одну и ту же величину. Все это позволяет сделать вывод, что при растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению. Эти напряжения можно определить по формуле:

σ = N / А,

где N – продольная сила, А – площадь поперечного сечения бруса.
3. Влияет ли форма поперечного сечения на значение напряжений, возникающих при растяжении и сжатии?

При растяжении или сжатии напряжения распределяются по поперечному сечению равномерно, геометрической характеристикой прочности и жесткости сечения является его площадь, форма сечения значения не имеет, все точки сечения равноопасны.
4. Что называется эпюрой нормальных сил и эпюрой нормальных напряжений?

Продольной силой называется равнодействующая всех внутренних нормальных сил, возникающих в сечении. График, показывающий изменение продольных сил по длине оси бруса, называется эпюрой продольных сил (эпюрой N).

Для наглядного изображения изменения нормальных напряжений в поперечных сечениях стержня (по его длине) строится эпюра нормальных напряжений. Осью этой эпюры является отрезок прямой, равный длине стержня и параллельный его оси. При стержне постоянного сечения эпюра нормальных напряжений имеет такой же вид, как и эпюра продольных сил (она отличается от неё лишь принятым масштабом). При стержне же переменного сечения вид этих двух эпюр различен; в частности, для стержня со ступенчатым законом изменения поперечных сечений эпюра нормальных напряжений имеет скачки не только в сечениях, в которых приложены сосредоточенные осевые нагрузки (где имеет скачки эпюра продольных сил), но и в местах изменения размеров поперечных сечений.
5. Для чего строят эпюры N ? Какое поперечное сечение бруса называется опасным?

В результате построений мы получим график (эпюру) распределения напряжений по каждому сечению бруса, визуальное исследование которого позволяет определить наиболее напряженный участок. Опасное сечение — это поперечное сечение, в котором действуют наибольшие внутренние усилия.
6. Что такое модуль продольной упругости материала, какова его размерность?

МОДУЛЕМ ПРОДОЛЬНОЙ УПРУГОСТИ материала называется коэффициент пропорциональности между нормальным напряжением и относительным упругим удлинением при линейном напряженном состоянии. [H/m²].
7. Что такое жесткость сечения бруса и жесткость бруса при растяжении (сжатии)?

Δl = N l / (E×А).

Произведение модуля упругости на площадь сечения Е×А, стоящее в знаменателе, называют жесткостью сечения при растяжении и сжатии; оно характеризует одновременно и физико-механические свойства материала бруса и геометрические размеры поперечного сечения этого бруса.

Приведенную выше формулу можно читать так: абсолютное удлинение или укорочение бруса прямо пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения бруса.
Выражение Е А / l называют жесткостью бруса при растяжении и сжатии.
8. Какова цель механических испытаний материалов?

Для определения физико - механических свойств материалов наиболее широко применяют статические испытания материалов на растяжение. Объясняется это тем, что механические характеристики, получаемые при испытании на растяжение, позволяют сравнительно точно определить поведение материала при других видах деформаций и этот вид испытаний, кроме того, наиболее легко осуществим.
9. Каковы характеристики пластичных свойств материалов?

Способность материала получать большие остаточные деформации, не разрушаясь, носит название пластичности. Мерой пластичности является удлинение d при разрыве. Чем больше d, тем более пластичным считается материал. Противоположным свойству пластичности является свойство хрупкости, т. е. способность материала разрушаться без образования заметных остаточных деформаций. Материалы, обладающие этим свойством, называются хрупкими. Для таких материалов величина удлинения при разрыве не превышает 2—5%, а в ряде случаев измеряется долями процента. Диаграмма растяжения хрупких материалов не имеет площадки текучести и зоны упрочнения.
10. Какие системы называют статически неопределимыми?

Статически неопределимыми называются такие системы, опорные реакции в которых и (или) внутренние усилия невозможно определить только из уравнений статики (уравнений равновесия).
11. Механические испытания материалов?

Испытание на растяжение — это относительно простой для понимания и объяснения метод испытания материала, и, возможно, его используют чаще остальных. При проведении этого испытания, образец материала растягивают вдоль продольной оси с помощью растягивающего приспособления испытательной машины.

Испытание на сжатие.

Испытания на растяжение проводить сложно, особенно, если материал хрупкий — в таких случаях наблюдается большой разброс результатов. Альтернативным методом оценки прочности материала является испытание на сжатие, которое легче провести, если материал хрупкий, так как в этом случае разброс результатов будет меньшим.

Испытание твердости — это измерение сопротивления поверхности материала воздействию инструмента, внедряемого или вдавливаемого в поверхность (индентеров), или режущего инструмента. Испытание твердости проводят для определения сопротивления материала царапанью или стиранию. Кроме того, существует приближенная зависимость между твердостью материала и пределом прочности на растяжение.

Испытание на ударную прочность — это оценка сопротивления материала мгновенному приложению нагрузки. Стандартный образец в виде балки с насечками подвергают воздействию импульсной нагрузки, создаваемой маятниковым копром.

Дата добавления: 2019-07-17; просмотров: 1830; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!