Применение уравнения Шрёдингера к свободному электрону.
Рассмотрим применение уравнения Шрёдингера к свободной частице, движущейся вдоль оси О X, например, к свободному электрону, т.е. к электрону, не испытывающему действия внешних полей. В этом случае потенциальная энергия свободно движущейся частицы U = 0, и уравнение Шрёдингера принимает вид:
. 
Для свободной частицы, движущейся вдоль оси О X волновая функция будет иметь следующий вид:
,
где 
-амплитуда волны. Круговая частота ω и волновое числоk связаны с полной энергией Е и импульсом p соотношениями: Е = ћω; p = ћ k, отсюда ω = 
; k = 
. Тогда волноваяфункцияпринимает вид:
.
Не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства 
означает, что все положения свободной частицы в пространстве являются равновероятными.
Энергия свободной частицы может принимать любые значения, следовательно, ее энергетический спектр явл непрерывным.
Применение уравнения Шрёдингера к электрону в потенциальной яме
Простейшим примером пространственно-ограниченного движения является одномерное движение квантовой частицы в силовом поле, имеющем вид очень глубокой потенциальной ямы с вертикальными стенками, график потенциальной энергии частицы U(x) имеет вид, показанный на рис .
Непроницаемость стенок выражается в неограниченном возрастании U ( x ) в точках х=0 и х= l . Частица может находиться лишь на участке 0<x<l Значение потенциальной энергии частицы в пределах этого участка U ( x )=0. Так как частица не выходит из промежутка 0<x < l , то вероятность ее обнаружения вне этого промежутка равна нулю, что возможно лишь в случае равенства нулю ее волновой функции вне этого участка. Следовательно, уравнение Шрёдингера должно быть дополнено граничными условиями: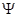 
(0)=0; 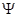(l)=0.
|
|
|
Решение уравнения Шредингера позволяет найти волновую функцию частицы в области 0<x < l. Пусть силовое поле не меняется с течением времени, поэтому воспользуемся уравнением для стационарных состояний, которое в случае U=0 принимает вид: 
.
Введем в уравнение волновое число: 
Тогда уравнение для одномерного случая приобретет вид: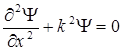 
.
Общим решениемданного однородногодифференциальногоуравнения второго порядка является волновая функция: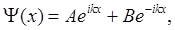 
где А и B - некоторые комплексные коэффициенты, не зависящие от x. Воспользуемся граничными условиями: Таккак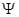 
(0)=0,то A + B =0 => B = - A .
С учетом того, что 
(l)=0, получим sin(kl)=0, откуда 
, k = 
, где n=0,1,2,3,... Случай n=0 должен быть отброшен, т.к. в этом случае получается, что 
(х)=0, т.е. вероятность обнаружения частицы внутри потенциальной ямы равна нулю. Однако с самого начала мы полагали, что частица локализована именно в области 0<x < l . Так как волновое число k принимает дискретный набор значений, то его записывают kn, а волновую функцию, зависящую от kn, записывают 
n. Вместо выражения 2iA удобно ввести новую комплексную постоянную С=2i A, тогда 
n(х)=C sin ( 
.
|
|
|
Для нахождения амплитуды С волновой функции воспользуемся условием нормировки: 
.
Так как 
, то 
, С= 
.
Таким образом: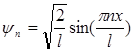 
.
Найдем энергию частицы находящейся в потенциальной яме через волновое число:
En = 
,
где n = 1, 2, 3….
Применение уравнения Шредингерак частице в потенциальной яме с бесконечно высокими стенками приводит к квантовым значениям энергии и координат, в то время как классическая механика наэнергию этой частицы лишних ограничений не накладывает. Кроме того, квантово-механическое рассмотрение этой задачи приводит к выводу, что частица в потенциальной яме с бесконечно высокими стенками не может иметь энергию меньшую, чем минимальная энергия, равная E1 = 
.
|
|
|
Дата добавления: 2019-07-17; просмотров: 184; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!