Корпускулярно-волновой дуализм.
Впервые проблема корпускулярно-волнового дуализма проявила себя при исследовании природы света – с одной стороны свет представляет собой поток мельчайших корпускул, что согласуется с законами геометрической оптики, а с другой стороны, свет – это частный случай электро-магнит волн. В итоге сложилась ситуация: сосуществование 2-х серьезных научных теорий, каждая их которых объяснила одни св-ва света, но не могла объяснить другие. Вместе эти 2 теории полностью дополняют друг друга.
Исаак Ньютон предложил считать свет потоком мельчайших корпускул.Это позволяло просто объяснить ряд наиболее характерных свойств
Свет – диалектическое единство противоположных свойств: он одновременно обладает свойствами непрерывных электромагнитных волн и дискретных фотонов.
При уменьшении длины волны все явственнее проявляются корпускулярные свойства. Волновые свойства коротковолнового излучения проявляются слабо (например, рентгеновское излучение). Наоборот, у длинноволнового инфракрасного излучения слабо проявляются квантовые свойства. Взаимосвязь между корпускулярными и волновыми свойствами света находит простое толкование при статистическом подходе к распространению света.
Взаимодействие фотонов с веществом, например, при прохождении света через дифракционную решетку приводит к перераспределению фотонов в пространстве и возникновению дифракционной картины на экране. Очевидно, что освещенность в различных точках экрана прямо пропорциональна вероятности попадания фотонов в эти точки экрана.
|
|
|
Но, с другой стороны, из волновых представлений видно, что освещенность пропорциональна интенсивности света I, которая в свою очередь,пропорциональна квадрату амплитудыволны А2. Отсюда вывод: квадрат амплитуды световой волны в какой-либо точке есть мера вероятности попадания фотонов в эту точку.
Давление света
Наличие у фотона импульса экспериментально проявляется в том, что свет оказывает давление на твердые тела и газы.
Давление света открыто русским ученым П.Н. Лебедевым в 1898 году.
В своих опытах он установил, что давление света зависит от интенсивности света и от отражающей способности тела. В опытах была использована легкая вертушка, имеющая черные и зеркальные лепестки, помещенная в вакуумированную колбу. Эксперимент показал, что на зеркальную поверхность свет оказывает большее давление, чем на зачерненную. Давление света на газы было измерено Лебедевым в 1909 году.
На основе выполненных экспериментов Лебедев сделал следующие выводы:
1. Давление света на зеркальную поверхность в два раза больше, чем давление на поверхность, полностью поглощающую свет.
|
|
|
2. Величина давления света с точностью до 20% соответствует значению, полученному теоретически Максвеллом для электромагнитных волн. В 1923 г. Герлах получил значение светового давления, совпадающего с теорией Максвелла с точностью до 2%, эксперимент проводился в высоком вакууме.
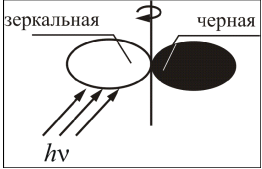
Рис. 18.1
Получим выражение для светового давления, исходя из квантовых свойств света.
Пусть поток фотонов с импульсом 
, модуль которого 
, падает по нормали к площадке 
и отражается с коэффициентом отражения 
(рис. 18.2).
Рис. 18.2
Интенсивность пучка падающего света пропорциональна концентрации 
фотонов (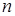 
– число фотонов в единице объема). Доля поглощенных фотонов от их полного числа равна 
. Каждый поглощенный фотон передает площадке импульс, численное значение которого 
, а отраженный фотон вследствие того, что импульс при отражении изменяется на противоположный ( 
), передает площадке импульс с численным значением 
.
Все фотоны, заключенные в объеме 
, достигнув площадки 
, изменят свои импульсы. Согласно второму закону Ньютона численное изменение результирующего импульса всех фотонов равно модулю импульса силы давления, т.е. 
, или
|
|
|
. (18.1)
Подставляя в (18.1) выражения для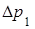 
, 
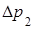и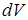 
и затем сокращая на 
, получим:
, 
,
,
=> , 
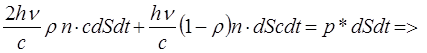, (18.2)
Где 
(18.3)
− объемная плотность энергии фотонов.
Интенсивность света I связана с объемной плотностью w0 световой энергии соотношением: 
. Тогда выражение (18.2) для давления света примет вид:
. (18.4)
Полученная формула (18.4) согласуется с выражением, полученным Маквеллом для давления, оказываемого плоской электромагнитной волной при падении ее на тело (см. формулу (4.10):
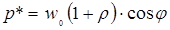, (18.5)
– угол падения волны на тело.
Таким образом, из корпускулярной теории следует, что световое излучение оказывает давление на материальные предметы, причем величина давления пропорциональна интенсивности излучения, что прекрасно подтверждается в экспериментах.
Эффект Комптона.
В 1923 г. А. Комптон, исследуя рассеяние рентгеновских лучей разными веществами, обнаружил, что в рассеянных лучах наряду с излучением первоначальной длины волны 
содержатся также лучи большей длины волны 
.
|
|
|
Разность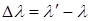 
оказалась зависящей только от угла 
, образуемого направлением рассеянного пучка. От длины волны λ и от природы рассеивающего вещества Δλ не зависит.
Все особенности эффекта Комптона можно объяснить, рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов с практически свободными электронами. Энергия связи с атомом таких электронов мала по сравнению с энергией, передаваемой ему рентгеновским квантом при столкновении.
Вычислим энергетические потери фотона при взаимодействии с электроном. Воспользуемся законами сохранения их полной энергии и полного импульса, подобно как для двух упруго взаимодействующих шаров.
Пусть 
– энергия фотона до столкновения,
– модуль импульса фотона до столкновения,
– энергия фотона после столкновения,
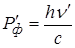– модуль импульс фотона после столкновения, тогда 
– модуль импульс электрона до столкновения,
– полная энергия электрона до столкновения,
, 
– масса покоя электрона,
– полная энергия движущегося электрона.
Согласно закону сохранения энергии:
. (18.8)
Закон сохранения импульса запишется в виде:
. (18.9)
Спроектируем векторное уравнение (18.9) на координатные оси 
и 
(рис. 18.4):
. (18.10)
После преобразования правой части уравнение приобретает вид:
,
или 
, т.к. 
, то
.
Пусть 
, - комптоновская длина волны
тогда 
- ур-е связывающее первонач длину волны с длиной волны
Комптоновская длина волны λC представляет собой изменение длины волны фотона при его рассеянии на угол 
.
Комптоновская длина волны аналогично вводится для протона, нейтрона и других элементарных частиц. Она определяется при замене массы покоя электрона на массу покоя соответствующей частицы.
Эффект Комптона подтвердил правильность квантовых представлений об электромагнитном излучении как о потоке фотонов и может рассматриваться как упругое столкновение двух частиц – фотона и электрона, при котором фотон передает электрону часть своей энергии (и импульса), вследствие чего его частота уменьшается, а длина волны увеличивается.
Дата добавления: 2019-07-17; просмотров: 191; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!