Фотохимия и резонансная теория катализа

⇐ ПредыдущаяСтр 17 из 18Следующая ⇒

Уточним формулы, которые должны описывать химические процессы, проходящие под действием резонансных фотонов, то есть такого излучения, которое соответствует спектру поглощения участников реакции. Мы будем исходить из основного состояния, так как многоступенчатые переходы приводят к тому же эффекту.

С другой стороны, среди всех возможных актов поглощения фотонов молекулами газов из основного состояния мы выделим только одну частоту, которую будем называть частотой фотоэффекта. Именно эту частоту, которая вызывает фотоэффект, молодой Альберт Эйнштейн еще в 1905 году посчитал важнейшей фотохимической константой. Однако, кто не хвалит Эйнштейна, но... кто его читает?

Совершенно очевидно, что имеется кардинальное различие между поглощением фотона с частотой меньшей, чем частота фотоэффекта, и частотой равной или превосходящей эту частоту.

Если частота меньше, то мы имеем физический эффект нагревания. Если частота равна или превосходит этот порог, то мы имеем дело с химической реакцией.

Так как отсутствует название для фотохимических реакций, где уравнения и константы равновесия пишутся с участием фотонов определенных длин волн или определенных частот, то теоретическое описание таких реакций мы будем называть фотоникой.

Запишем традиционно химическую реакцию между атомами натрия и хлопа:

Na ⁰ + Cl ⁰ = NaCl + Q (1)

Запишем константу равновесия:

(2)

Здесь Q - тепловой эффект реакции.

Как отмечалось выше, эта запись химической реакции страдает отсутствием полноты. В ней нет места излучению, которое является непременным участником любой химической реакции. Фотохимическое равновесие предполагает наличие непрерывного потока лучистой энергии с заданной частотой или длиной волны. Физический смысл новой константы равновесия — поперечное сечение захвата фотона.

Аналогичное понятие пока существует лишь в ядерной физике, где поперечное сечение захвата нейтрона зависит от энергии нейтрона, которую тоже (по соотношению де Бройля) можно рассматривать как частоту или длину волны, связанную с нейтроном. Подобно тому, как существуют резонансы в ядерной физике, существуют подобные резонансы и в обычной химии: спектр резонансных частот и есть действительный спектр соответствующей молекулы.

Хотя это было очень давно, но один из физиков-теоретиков отрицал возможность поглощения фотонов отдельными атомами, ссылаясь на геометрическую оптику: длина волны во много раз больше поперечного сечения любого атома, и такая волна "должна огибать препятствие столь малого размера". Мне пришлось сослаться на атомный абсорбционный анализ, где излучение натриевой лампы почти в три тысячи раз больше размера атома или иона натрия, но поперечное сечение захвата столь велико, что резонансная линия сильно поглощается натрием из пламени, расположенного между лампой и приемником излучения. Поскольку речь идет о весьма уважаемом физике-теоретике, то можно понять, сколь маловероятно знание такого рода фактов из физических методов химического анализа для рядовых физиков. Другим примером являются оптико-акустические газоанализаторы. Это приборы, которые преобразуют резонансное излучение, различное в различных камерах, в колебания мембраны, то есть в звуковой эффект.

Запишем уравнение реакции между фотоном и нейтральным атомом натрия. Полная запись с участием фотонов приобретает вид:

Na ⁰ + 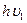= Na ⁺ + e ^- (3)

Сделанная запись показывает, что атом натрия (свободный) не может
сам отдать электрон и превратиться в ион натрия, так как отрыв электрона требует выполнения "работы выхода", которая и совершается под действием фотона с частотой . Нижний индекс - -1 - характеризует частоту, которая необходима для отрыва электрона.

Эта частота является важнейшей константой для всей фотохимии, так как ее физический смысл, имеющий теоретическое обоснование только для спектра водорода, носит название константы Ридберга. Теоретического подхода к вычислению аналогичной величины для самых разнообразных атомов и молекул не существует. Сами же эти величины легко определяются экспериментально, а наличие таблиц этих величин квантовой химии позволит надеяться на создание адекватной теории.

Желая указать связь этой константы с константой Ридберга, мы будем называть ее "Рид-с", где буква "с", написанная через дефис, означает специфичность этой константы, определяемой из условий реакции.

Запишем константу фотохимического равновесия для этой стадии химического процесса:

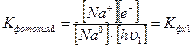(4)

Запись справа является сокращением записи константы слева, так как последняя требует слишком много букв. Но это не значит, что у новых констант фотохимического равновесия не было отличия от традиционной записи.

Запишем уравнение реакции между свободным электроном и нейтральным атомом хлора. Полная запись с участием фотонов приобретает вид:

Cl ⁰ + e ^- = Cl 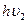^- + (5)

Здесь захват электрона нейтральным атомом хлора связан с выделением "энергии сродства к электрону", которая высвечивается в виде фотона с частотой .

Запишем константу фотохимического равновесия для этой стадии химического процесса:

(6)

Последняя стадия этого химического процесса состоит в образовании связи между ионами натрия и хлора, а энергия образовавшейся связи выделяется в виде фотона с частотой .

Na ⁺ + Cl ^- = NaCl + (7)

Запишем константу фотохимического равновесия и для этой стадии химического процесса:

(8)

Последняя константа фотохимического равновесия отличается от обычной константы, принятой в химии, тем, что в знаменателе стоят ионы, а не свободные атомы натрия и хлора. Но, пользуясь выражениями (4) и (6), можно совершить замену. Используя формулу (4), находим выражение для иона натрия, фигурирующего в формуле (8):

(4*)

Подставим это значение в формулу (8) и получим:

(8*)

Подобным образом из формулы (6) находим:

(6*)

Подставим и это значение в формулу (8*):

(8**)

Нетрудно видеть, что перенося в левую часть формулы (8**) все, что не входит в запись формулы (2), и сокращая концентрацию электронов, получим:

(2**)

Полученный результат показывает, что полное выражение урезанной константы химического равновесия игнорирует излучение, которое используется в химическом процессе.

Окончательно — полное выражение для константы равновесия имеет вид:

(9)

Но до сих пор используемая урезанная запись не приводила к особым недоразумениям. Это так и будет, если излучение соответствует формуле Планка, дающей распределение излучения в спектре абсолютно черного тела.

Если же под действием внешних источников плотность излучения
отличается от той, что следует из формулы Планка, то мы и обнаруживаем несостоятельность обычной константы. Эта возможность и используется при подаче резонансного излучения в сферу реакции.

Мы еще не выразили тепловой эффект химической реакции Q через участников реакции при полном описании. Нетрудно видеть, что тепловой эффект химической реакции легко выражается через фотоны. Алгебраическая сумма поглощенных и излученных фотонов дает выражение для теплового эффекта реакции.

(10)

где

Q - тепловой эффект реакции;

N - число Авогадро;

- энергия фотонов, участвующих в реакции.

В нашем описании отсутствует понятие энергии активации; роль этой величины играет энергия первого фотона, обладающего частотой фотоэффекта. В экзотермических реакциях энергия этого фотона меньше, чем энергия выделившихся фотонов. В эндотермических реакциях энергия первого фотона больше, чем энергия выделившихся фотонов. Из этого следует, что эндотермические реакции предполагают использование дальнего ультрафиолета, которого сейчас на поверхности планеты практически нет. По утверждению В.И. Вернадского, вся атмосфера Земли биогенного происхождения. Это означает, что в отсутствии Жизни этот ультрафиолет доходил до поверхности планеты и мог обеспечить протекание реакций синтеза органических веществ из неорганических.

5. Фантом энтропии и мифы экономических "теорий"

Если бы автор оставался в пределах тех научных результатов, которые известны современной науке, то ничего существенно нового от него получить (услышать, прочитать) было бы невозможно.

Я называю любую научную позицию либо новой, либо старой.

Для новой научной позиции необходимо указать те положения, которых в современной науке не было, а эта позиция отличает автора от всех известных работ.

Если этих новых положений нет, то мы имеем дело лишь с перестановкой порядка слов в известных (существующих) теориях.

Для старой научной позиции характерно то, что в рамках той или иной теории выводимо из ранее известных законов (или аксиом — в математическом описании). Более того, автор старой научной позиции даже не всегда может назвать те аксиомы, на которых построена используемая им прикладная теория.

Мне самому приходилось и приходится сталкиваться с людьми, которые считают, что они приходят ко мне с "новыми" научными результатами. В этом случае мне приходится задавать один и тот же вопрос: "Что вам известно такого, что неизвестно в современной науке"? ,а1 Если мне не могут назвать таких положений, то я знаю, что от перестановки слов известной теории ничего нового получить нельзя. Очевидно, что спрашивая это у других людей, я сам должен отвечать на тот же вопрос. Поскольку речь идет о математической (или теоретической) физике, то все правильно сделанные теории можно передать машинной информационной системе, а последняя, при задании соответствующих условий, должна выдавать на выходе вычислительного комплекса научные предсказания (подтверждаемые практикой), выводимые из предпосылок данной теории.

Вообще говоря, нельзя настаивать на положении, как на новом, то есть таком, что у этого положения не было научных предшественников, которые по тем или иным причинам не получили признания из-за ограниченности научных данных, которыми располагали предшественники. - Именно это положение и приводит к пословице: "Новое — это хорошо забытое старое".

Я назову три положения, которые отличают автора от многочисленных предшественников:

1) автор пользуется стандартом или техническими условиями на приемку прикладных научных теорий;

2) автор использует закон сохранения мощности (установленный еще Лагранжем и отсутствующий в учебниках физики высшей школы не только в России, но и в Европе и Америке, однако известный в Японии);

3) автор пользуется своим определением понятия жизнь, с учетом введенного им различия в аксиоматике живой и неживой природы.

Если все указанные положения не являются новыми для читателя, причем во всей совокупности, то для такого читателя этот текст не несет новой информации.

Я назвал три положения, которые и обеспечивают особенность нового в работах автора. Необходимо знание этих трех положений, чтобы новая физика химических процессов приобрела достойный вид. Следует отметить, что всякая новая теория включает классические теории на правах частного случая. Такой эффект достигается, когда в рамках старой теории, имеющей свои границы применимости, определяемые аксиомами, одна из аксиом отрицается, а это позволяет распространить теорию на область, в которой старая теория была несостоятельна. В области чистой математики такой пример следует из работ Н.И.Лобачевского и Я. Бойяи.

Прежде чем излагать доказательство истинности трех особенных положений, которыми автор пользуется в своих работах, мы хотели бы обратить внимание на одну физическую константу, известную как константа Больцмана. Константа Больцмана k =1,38054 х 10^-16 эрг х град^-1 фигурирует в физике как постоянная и связывает классическую термодинамику со статистической физикой как в классическом случае, так и в квантовой механике. Действительно ли это физическая постоянная?

Нетрудно показать, что это не так. Достаточно было бы в истории физики разбить шкалу термометра между точкой плавления льда и точкой кипения воды на десять или на тысячу частей, как эта константа либо увеличилась бы в десять раз, либо уменьшилась бы в десять раз. Слепая уверенность в том, что эта величина от Бога, не позволяет увидеть в этой константе соглашения, принятого в истории физики. Считать эту величину константой — это не увидеть другие, не менее важные дефекты в физической теории.

Известно, что в школьной физике, да и в учебниках высшей школы, фигурирует формула:

(1)

Здесь

Е - энергия, накопленная в форме тепла в газе;

р - давление газа;

V - объем газа;

R - газовая постоянная;

Т - температура газа.

Вообще говоря, такую зависимость теоретическая физика имеет только для "идеального газа".

Через некоторое время, когда было обнаружено, что теплоемкость газов различна и зависит от числа степеней свободы (которые считались определяемыми числом атомов в молекуле), было принято соглашение относить постоянную К не к одному молю газа, а относить на одну степень свободы молекулы. Это соглашение превратило газовую постоянную в константу Больцмана, которая выражается отношением газовой постоянной к числу молекул в грамм-молекуле:

k = R : N = 1,38054 х 10^-16 эрг/град (2)

Некоторое время спустя эту константу начали умножать на множитель, зависящий от сложности молекул, используя представление о степени свободы. Формула (1) приобретает вид:

(3)

где

Е - энергия газа;

р - давление газа

V - объем газа

kN = R - газовая постоянная, отнесенная к одной молекуле;

n - множитель, учитывающий число степеней свободы и принимающий значения: 3/2; 5/2; 7/2....

Некоторое время спустя снова пришлось корректировать формулу теплоемкости газа, которая оказалась сама зависящей от температуры. Традиционный математический прием аппроксимации изменяющейся величины — это разложение в ряд по степеням независимой переменной. Возвращаясь снова к газовой постоянной (разложение в степенной ряд лишает эту величину статуса постоянной — теперь она переменная, представляемая суммой ряда) запишем разложение в ряд по степеням температуры:

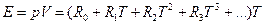(4)

Мы получили новый вид функции, выражающий изменение теплоемкости газа в зависимости от температуры, то есть мы установили, что газовая "постоянная" не является "постоянной", а изменяется с изменением температуры. Формула (4) имеет очень громоздкий вид. Для уменьшения числа членов в степенном ряду можно заменить этот ряд некоторой новой буквой, заменяющей этот ряд. Выбираем для этого обозначения букву 5. Имеем:

(5)

Подставляем это значение в формулу (4), но не будет забывать, что скрывается за символом S:

(6)

Сравним формулу (6) с формулой (1) и зададимся вопросом: "На какой же формуле базируется статистическая физика?" Ведь нельзя ПОСТУЛИРОВАТЬ в рамках одной и той же теории в качестве ИСТИННЫХ - ДВЕ различные формулы для одной и той же энергии газа. Образованный физик сразу же поймет, что буква S выбрана не случайно - да, это и есть ЭНТРОПИЯ. Нетрудно убедиться в этом, записывая выражение для "свободной энергии":

(7)

Дифференцируя это выражение, мы получим хорошо известную формулу изменения свободной энергии:

(8)

Интеграл от этого полного дифференциала возвращает нас к формулам (7) и (6).

Для начала заметим, что для равновесных систем свободная энергия равна нулю. С другой стороны, обращаясь к формуле (1) и к формуле (6), зададимся не традиционным вопросом: "Что такое энтропия", а вопросом: "Что мы измеряем, когда измеряем температуру".

Ведь измерение температуры задавалось правилом, что при постоянном давлении между температурой и объемом термометрического тела существует линейная зависимость, которая и выражается газовой постоянной. Это означает, что приращение энергии газа выражается через приращение температуры. В настоящее время мы знаем целое множество температур: цветовая, вращательная, колебательная и другие и плюс к этому "абсолютная отрицательная температура".

Небольшое размышление показывает, что исторический термин "температура" связан с изменением объема термометрического тела и предположением о линейной зависимости энергии тела от его объема.

В этом случае в формуле (1) приращение энергии можно выразить через приращение объема, то есть:

(1*)

Здесь мы показываем, что измеряемой физической величиной, которую измеряла классическая физика и называла температурой, была величина изменения объема термометрического тела, что мы делаем и в наши дни при использовании термометров расширения. Обратимся к формуле (6) – здесь та же ситуация, только вместо буквы R стоит буква S. Но физический смысл остается без изменения - эта теперь переменная величина связывает между собою энергию и объем термометрического тела. Имеем:

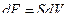(6*)

При обсуждении парадоксального положения, связанного с использованием в основаниях статистической физики ДВУХ ВЗАИМОИСКЛЮЧАЮЩИХ ФОРМУЛ, мне приходилось слышать, что величина S существенно ПОЛОЖИТЕЛЬНА. И это положение не выдерживает критики: достаточно заполнить термометр расширения водой и нагревать от 0⁰ до 4⁰ по Цельсию, чтобы получить положительную величину прироста энергии (при уменьшающемся объеме) необходимо считать значение S - ОТРИЦАТЕЛЬНЫМ.

Поскольку мы теперь знакомы и с отрицательными абсолютными температурами, то автор еще в 1961 году рассматривал в одной из своих публикаций абсолютные отрицательные температуры при фазовых переходах в окислительно-восстановительном потенциале и при фотохимических реакциях.

Поскольку при публикации необходимо было отказаться от формул, то мы их воспроизведем здесь.

Рассматривая убывающую часть функции распределения скоростей (соответственно энергий) молекул при заданной температуре имеем общее выражение для числа молекул в зависимости от их энергии:

(9)

Это соотношение и задает зависимость между числом молекул, находящихся на нижнем и верхнем энергетическом уровне при заданной температуре. Используем это выражение для вычисления числа молекул на нижнем и верхнем энергетическом уровнях. Полагая, что Е₁ меньше, чем энергия Е₂, будем иметь:

(10)

Мы записали выражение для доли молекул, находящихся на нижнем энергетическом уровне. Сделаем то же самое для доли молекул на верхнем энергетическом уровне:

(11)

Возьмем отношение числа молекул на нижнем уровне к числу молекул на верхнем энергетическом уровне. Учитывая, что физический смысл левых частей выражений (10) и (11) - есть просто ЧИСЛА молекул на соответствующих уровнях, можно отказаться от символа d, который заменял отсутствующую у меня букву греческого алфавита дельта. Поскольку общее число молекул N₀ сократится, мы будем иметь:

(12)

Полученное выражение показывает, что в числителе стоит разность энергий верхнего и нижнего энергетических уровней, то есть величина существенно положительная. Для того, чтобы освободиться от вхождения ехр, прологарифмируем обе части соотношения (12).

Получим:

(13)

Левую часть выражения (13) можно представить как разность логарифмов:

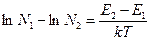(14)

Наш следующий шаг состоит в получении зависимости температуры от населенности верхнего и нижнего энергетических уровней (такой способ измерения температуры применяется в спектроскопии, где рассматривается отношение интенсивностей двух спектральных линий — соответствующих различным значениям энергии). Окончательно имеем:

(15)

Не сразу бросается в глаза, что выражение в скобках, характеризующее разницу логарифмов частиц на нижнем и верхнем уровнях, наша старая знакомая энтропия, точнее ее дифференциал, умноженный на константу Больцмана. Если разницу энергий обозначить как dQ , не использовать постоянной Больцмана, то выражение (15) преобразуется в:

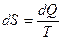(16)

Этого следовало ожидать, так как в статистической термодинамике в полученное выражение от логарифма функции распределения множитель к принято добавлять "руками", поскольку эта размерная физическая величина не присутствует в стандартной теории вероятностей.

Вернемся к выражению (15), где фазовые переходы, редокс-потенциал и фотохимические процессы (типа фотосинтеза) связаны с абсолютными отрицательными температурами, что и было отмечено некоторыми учеными через два года после публикации автора.

Рассмотрим превращение льда в воду. Обычный термометр расширения на протяжении всего фазового перехода показывает нуль градусов по Цельсию. Совсем иначе ведет себя "статистический термометр". Естественно, что молекула воды в состоянии льда находится на более низком энергетическом уровне, чем тогда, когда она находится в жидкой фазе,
Разница энергий есть то, что принято называть скрытой теплотой плавления. Пока в смеси воды со льдом число молекул в виде льда много больше, чем молекул в жидкой фазе, и числитель и знаменатель выражения (15) положительны и температура тоже положительна. В тот момент, когда число молекул в твердой и жидкой фазе становятся равными друг другу, знаменатель выражения (15) обращается в нуль и вычисляемое значение температуры становится равным бесконечности. По мере нарастания числа молекул в жидкой фазе, теперь уже численно доминирующих твердую фазу, мы идем через область абсолютных отрицательных температур. После превращения всего льда в воду функция температуры со
стороны отрицательных значений устремляется к нулю и здесь претерпевает разрыв, так как логарифм нуля (для твердой фазы) равен бесконечности.

Аналогичное положение имеет место при рассмотрении окислительно-восстановительных потенциалов. Если мы имеем раствор, в котором находятся ионы двух- и трехвалентного железа, то когда число молекул того и другого рода равны друг другу, то вычисляемая температура равна бесконечности, а обычные химики называют это состояние "нормальным редокс-потенциалом".

Вообще, абсолютные отрицательные температуры появляются там, где возможно устойчивое существование микрочастиц на верхнем и нижнем энергетических уровнях — приведенные выше фазовый переход и окислительно-восстановительный потенциал (железо-3 — более высокий энергетический уровень, чем железо-2). Наконец, фотосинтез: продукты фотосинтеза занимают более высокий энергетический уровень, чем исходные вещества.

Известна работа Э. Шредингера: "Что такое жизнь с точки зрения физики?". В ней Шредингер делает заявление, что растение питается "отрицательной энтропией" — и все поверили ему. Автор проверил это утверждение прямым расчетом и оказалось, что Шредингер прав тогда и только тогда, когда температура листа растения имеет абсолютное отрицательное значение. Таким образом эффект "отрицательной энтропии" имеет ту же природу, что и абсолютные отрицательные температуры.

6. Обратимость "необратимых" реакций - возможна регенерация

Дата добавления: 2019-07-17; просмотров: 243; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 9 10 11 12 13 14 15 161718 Следующая ⇒

Мы поможем в написании ваших работ!