Закон распределения вероятностей дискретной случайной величины. Ряд распределения вероятностей дискретной случайной величины. Многоугольник распределения.
Законом распределения дискретных случайных величин называется перечень ее возможных значений и соответствующих им вероятностей.
Формы распределения:
1) Таблица (ряд) распределения, где pi=Р(Х=xi)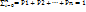 
2) Многоугольник распределения
Функция распределения вероятностей дискретной случайной величины, ее свойства и график
Функцией распределения дискретной случайной величины называется функция F(x), определяющая для каждого значения «х» вероятность того, что дискретная случайная величина примет значение < х: F(x)=Р(Х<х)
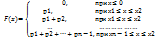
Свойства функций распределения:
1) Значение ф-ции распределения принадлежит отрезку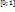 
0≤F(x)≤1
2) Ф-ция распределения является неубывающей функцией, если х1<х2, то F(x1)<F(x2)
3) Ф-ция распределения непрерывна слева
Числовые характеристики дискретной случайной величины: мат. ожидание, дисперсия и среднеквадратическое отклонение
Математическим ожиданием дискретных случайных величин «х» называется сумма произведений ее возможных значений на соответствующие вероятности. M(X)=x1p1+x2p2+…+xnpn
Дисперсией дискретной случайной величины «х» называют математическое ожидание квадрата отклонения случайной величины X от ее математического ожидания. D(x)=M[x-M(x)]2 или D(x)=M(x)2-[M(x)]2
Среднее квадратичное отклонение. σ(x)=√D(х)
Математическое ожидание дискретной случайной величины (ДСВ). Свойства математического ожидания ДСВ
|
|
|
Мат. ожидание ДСВ «х» - это сумма произведений ее возможных значений на соответствующие вероятности. M(X)=x1p1+x2p2+…+xnpn
Свойства мат. ожидания:
1. M(CX) = CM(X); M(C) = C, где С -произвольная постоянная величина
2. M(X1X2…Xn) = M(X1)M(X2)…M(Xn), если X1, X2, …, Xn – взаимно независимые случайные величины.
3. M(X1+X2+…+Xn) = M(X1)+M(X2)+…+M(Xn)
4. M(X) = np, где Х – дискретная случайная величина, n – число испытаний с биноминальным законом распределения, р – вероятность появления события в одном испытании.
Дисперсия дискретной случайной величины (ДСВ). Свойства дисперсии ДСВ.
Дисперсией ДСВ «х» называют математическое ожидание квадрата отклонения случайной величины «х» от ее математического ожидания.
D(x)=M[x-M(x)]2 или D(x)=M(x)2-[M(x)]2
Свойства дисперсии:
1. D(C) = 0; D(CX) = C2D(X), где С - произвольная постоянная
2. D(X1+X2+…+Xn)=D(X1)+D(X2)+…+D(Xn), где Х – независимые случайные величины.
3. D(X) = npq, где X ДСВ с биноминальным законом распределения, n – число испытаний, pq – верятность появления и вероятность непоявления события в одном испытании соответственно.
4. σ(Х) =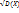 
, где σ(Х) – это среднее квадратичное отклонение.
Вероятность появления хотя бы одного события. Вероятность появления только одного события.
В некоторых случая вероятность события удобнее подсчитывать как вероятность противоположного др. событию и определяется по формуле
|
|
|
P(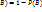 
.
Вероятность появления только одного из 2-х совместных событий А и В расчитывается по формуле
P(A+B) = P(A×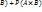 
23.Классическая и геометрическая схемы определения вероятностей.
Классическая: Вероятность события А рассчитывается по формуле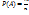 
, где m – число тех исходов испытания, которые благоприятствуют событию А, n – число всех исходов испытания.
Опыт имеет n возможных исходов, которые равно возможны, несовместны и образуют полную группу.
Геометрическая. Вероятность случайного события равна отношению меры области (длины, площади, объема), благоприятствующей данному событию к мере, соответствующей всевозможным исходным данным. Рассчитывается по формуле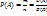 
, где D – мера области, А – область которая благоприятствует появлению события, Ω – вся плоскость.
1. Основные понятия теории множеств. Способы задания множеств. Привести примеры.
2. Понятие множества. Отношения между множествами, их представление с помощью диаграмм Эйлера-Венна. Привести примеры.
3. Понятие множества. Основные операции над множествами. Изображение их результатов с помощью диаграмм Эйлера-Венна. Привести примеры.
|
|
|
4. Основные понятия математической логики (простые и составные высказывания, их логические значения).
5. Логические операции над высказываниями. Привести примеры.
6. Определение матрицы. Виды матриц. Привести примеры.
7. Основные операции над матрицами. Привести примеры.
8. Определители. Вычисление определителей 2-го и 3-го порядков. Основные свойства определителей. Привести примеры.
9. Система m линейных уравнений с n неизвестными. Определение решения системы. Совместные и несовместные, определенные и неопределенные системы линейных уравнений. Привести примеры.
10. Система n линейных уравнений с n неизвестными. Правило Крамера. Привести пример.
11. Базисные решения системы линейных уравнений. Метод Гаусса. Привести пример.
12. Понятие линейного программирования. Математическая постановка общей и основной задачи линейного программирования.
13. Разрешимость задачи линейного программирования (ЗЛП). Допустимое решение ЗЛП. Область допустимых решений ЗЛП. Оптимальное решение ЗЛП.
14. Графический метод решения задачи линейного программирования с двумя переменными. Привести пример.
15. Постановка транспортной задачи закрытого типа. Разрешимость транспортной задачи. Понятия допустимого, опорного, вырожденного и оптимального планов. Привести примеры.
|
|
|
16. Методы составления опорных планов: метод северо-западного угла и метод минимального элемента. Привести пример.
17. Решение транспортной задачи методом потенциалов. Привести пример.
18. Понятие комбинаторики. Основные правила комбинаторики: правила суммы и произведения. Привести примеры.
19. Основные виды комбинаций (с повторениями и без повторений): перестановки, размещения, сочетания. Привести примеры.
20. Основные понятия теории вероятностей: опыт, серия опытов, событие, вероятность. Детерминированное и случайное события. Привести примеры.
21. Основные виды событий: совместные и несовместные, зависимые и независимые, равновозможные. Привести примеры.
22. Полная группа событий. Условие нормировки. Противоположные события. Привести примеры.
23. Классическая и геометрическая схемы определения вероятностей. Привести примеры.
24. Произведение событий. Правила умножения вероятностей зависимых и независимых событий. Привести примеры.
25. Сумма событий (совместных и несовместных). Правила сложения вероятностей совместных и несовместных событий. Привести примеры.
26. Вероятность появления хотя бы одного события. Вероятность появления только одного события. Привести примеры.
27. Формула полной вероятности. Формула Байеса. Привести примеры.
28. Схема Бернулли и приближенные формулы Пуассона и Муавра-Лапласа.
29. Понятие случайной величины. Классификация случайных величин (дискретные и непрерывные). Привести примеры.
30. Закон распределения вероятностей дискретной случайной величины. Ряд распределения вероятностей дискретной случайной величины. Многоугольник распределения. Привести примеры.
31. Функция распределения вероятностей дискретной случайной величины, ее свойства и график. Привести примеры.
32. Числовые характеристики дискретной случайной величины: математическое ожидание, дисперсия и среднеквадратическое отклонение. Привести примеры.
33. Математическое ожидание дискретной случайной величины (ДСВ). Свойства математического ожидания ДСВ. Привести примеры.
34. Дисперсия дискретной случайной величины (ДСВ). Свойства дисперсии ДСВ. Привести примеры.
35. Биномиальный и пуассоновский законы распределения вероятностей дискретной случайной величины, их числовые характеристики.
36. Основные понятия и определения математической статистики. Генеральная и выборочная совокупности. Объем совокупности. Типы выборок. Способы образования выборок. Привести пример.
37. Первичная обработка статистических данных. Вариационный ряд. Абсолютная и относительная частоты. Условия нормировки. Статистическое распределение выборки. Интервальное распределение выборки. Привести пример.
38. Эмпирическая функция распределения, ее свойства и график. Полигон частот и гистограмма. Привести пример.
39. Статистическая оценка вероятности появления случайной величины. Несмещенная, смещенная, эффективная и состоятельная оценки.
40. Точечные оценки вероятностных характеристик: выборочная средняя, выборочная дисперсия, выборочное среднеквадратическое отклонение.
Дата добавления: 2019-07-15; просмотров: 294; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!