Содержание ограничений по выражению требований общества к товаропроизводителям.

⇐ ПредыдущаяСтр 19 из 20Следующая ⇒

Методика построения матрицы экономико-математической задачи.

Матрицей A=A_mn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.

Элементы матрицы a_ij, у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a₁₁, a₂₂,..., a_nn .

Равенство матриц.

A=B, если порядки матриц A и B одинаковы и a_ij=b_ij (i=1,2,...,m; j=1,2,...,n)

Действия над матрицами.

1. Сложение матриц - поэлементная операция

2. Вычитание матриц - поэлементная операция

3. Произведение матрицы на число - поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B) A_mk*B_kn=C_mn причем каждый элемент с_ij матрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

Покажем операцию умножения матриц на примере

5. Возведение в степень

m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A'

Свойства опрераций над матрицами

A+B=B+A, ( A + B )+ C = A +( B + C ), λ( A + B )=λ A +λ B , A ( B + C )= AB + AC , ( A + B ) C = AC + BC , λ( AB )=(λ A ) B = A (λ B ), A ( BC )=( AB ) C , ( A ')'= A , (λ A )'=λ( A )', ( A + B )'= A '+ B ', (AB)'=B'A'

Виды матриц

1. Прямоугольные: m и n - произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1. Например

5. Диагональная матрица: m=n и a_ij=0, если i≠j. Например

6. Единичная матрица: m=n и

7. Нулевая матрица: a_ij=0, i=1,2,...,m

j=1,2,...,n

Методика расчета параметров ЭМ на ПК.

При обработке информации на компьютере выбор вида уравнения регрессии обычно осуществляется экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии d_oct, рассчитанной при разных моделях.

Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии 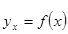, то фактические значения результативного признака совпадают с теоретическими , т. е. они полностью обусловлены влиянием фактора х. В этом случае остаточная дисперсия D_OC_Т = 0. В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих не учитываемых в уравнении регрессии факторов. Иными словами, имеют место отклонения фактических данных от теоретических . Величина этих отклонений и лежит в основе расчета остаточной дисперсии:

Чем меньше величина остаточной дисперсии, тем в меньшей мере наблюдается влияние прочих не учитываемых в уравнении регрессии факторов лучше уравнение регрессии подходит к исходным данным. При обработке статистических данных на компьютере перебираются разные математические функции в автоматическом режиме и из них выбирается та, для которой остаточная дисперсия является наименьшей.

Если остаточная дисперсия оказывается примерно одинаковой для нескольких функций, то на практике предпочтение отдается более простым видам функций, ибо они в большей степени поддаются интерпретации и требуют меньшего объема наблюдений. Результаты многих исследований подтверждают, что число наблюдений должно в 6-7 раз превышать число рассчитываемых параметров при переменной х. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при х должен рассчитываться хотя бы по 7 наблюдениям. Значит, если мы выбираем параболу второй степени

то требуется объем информации уже не менее 14 наблюдений. Учитывая, что эконометрические модели часто строятся по весьма ограниченным данным: объем выборки редко превышает 10-15 членов, при выборе спецификации

Методика решения ЭММ на ПК.

Экономико-математические методы в сочетании с применением персональных компьютеров позволяют в ряде случаев при доступных затратах получать рациональные управленческие решения. Трудности использования ЭВМ связаны со многими причинами, по прежде всего из-за сложности экономических процессов и явлений, затрудняющей их формализацию моделями.

В настоящее время апробированы математические методы решения следующих задач подготовки управленческих решений

— оптимизация выпуска однородной продукции при нескольких технологических способах, что обеспечивает получение максимальной общей прибыли при ограничениях на объемы ресурсов и запасов и на производство единицы продукции;

— оптимизация производственной программы при заданной технологии, когда находятся объемы выпуска продукции /-го вида, обеспечивающие получение максимальной прибыли при заданных значениях расходов /-го ресурса и величины прибыли на единицу продукцииу-го вида;

— оптимизация состава парка машин разного типа, когда известны их стоимость и производительность при выполнении конкретных работ, обеспечивающих выполнение плана при минимуме затрат на покупку этих машин;

— определение оптимальной загрузки оборудования для достижения минимума себестоимости продукции при известных стоимости и производительности этого оборудования;

— оптимальное размещение организации — поставщика продукции, при котором минимизируется число тонно-километров перевозок к потребителям с заданным потреблением и расположением;

— распределение капитальных вложений для объектов незавершенного строительства, по каждому из которых известны предыдущие капитальные вложения и максимально возможные для освоения их объемы в планируемом году при соблюдении предельного значения общего фонда финансирования незавершенного строительства,

— прикрепление потребителей к поставщикам таким образом, чтобы суммарные транспортные расходы по доставке всей продукции потребителям были минимальны;

— назначение по объектам работников различных специальностей для достижения максимальной производительности;

— расчет временных и ресурсных параметров сетевых моделей. Экономико-математическая модель — это описание, отображающее экономический процесс или явление с помощью математических выражений (уравнений, функций, неравенств, тождеств), имитирующих поведение моделируемого объекта в заданных или возможных условиях его реального существования.

Дата добавления: 2019-07-15; просмотров: 588; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 11 12 13 14 15 16 17 181920 Следующая ⇒

Мы поможем в написании ваших работ!