Параллельное соединение четырехполюсников.

При параллельном соединении как входные, так и выходные зажимы составляющих четырехполюсников соединяются параллельно (рис. 3).

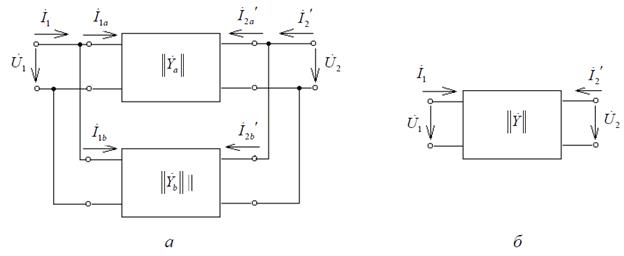
Рисунок 3

Запишем уравнения исходных четырехполюсников (рис. 3, а) в сис­теме 7-параметров:

 

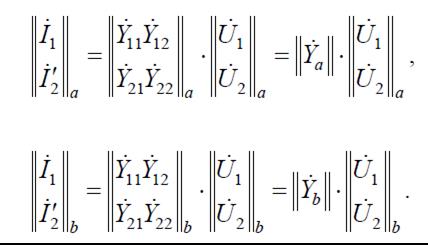
Напряжения и токи на входе и выходе эквивалентного четырехполюс­ника (рис.3, б):

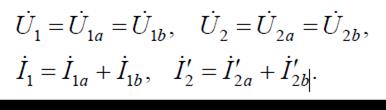
Следовательно,

 

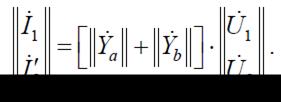
Матрица проводпмостей эквивалентного четырехполюсника (рис. 3, б)

 

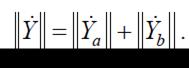
Последовательно-параллельное соединение четырехполюсников.

В данном случае входные зажимы составляющих четырехполюсников соединяются последовательно. а выходные - параллельно (рис. 4).

Запишем систему уравнений четырехполюсников в //-параметрах:

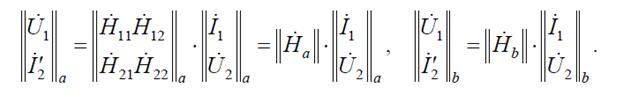
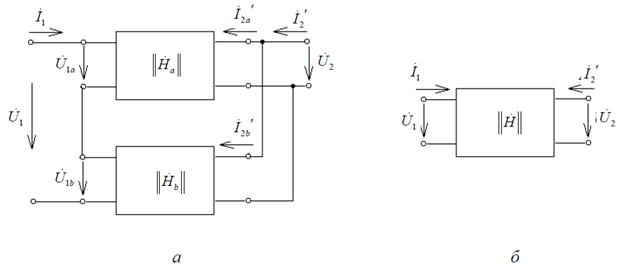
Рисунок 4

Для эквивалентного четырехполюсника (рис. 4, б)выполняются со­отношения:

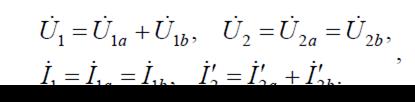
Таким образом,

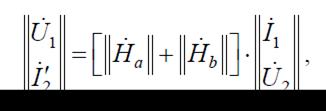
т. е. матрица H-параметров эквивалентного четырехполюсника:

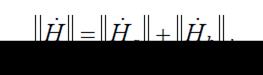
Параллельно-последовательное соединение четырехполюсников.

В рассматриваемой схеме (рис. 5, а)входные зажимы составляющих четырехполюсников соединены параллельно, а выходные - последовательно.

Уравнения четырехполюсников в данном случае удобно представить в системе G-параметров

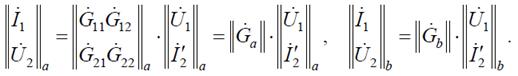
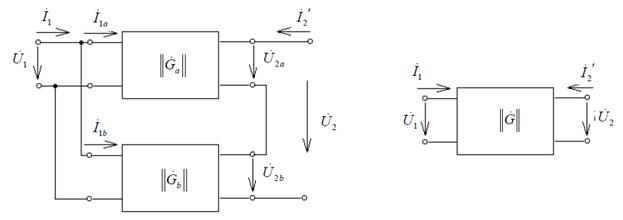
Рисунок 5

Из схемы (рис.5, а)следует, что

 

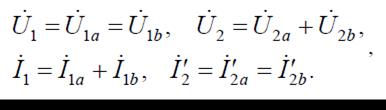
Для эквивалентного четырехполюсника (рис. 5, б) получим:

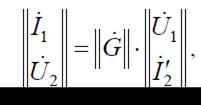
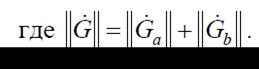
Следует отметить, что правила нахождения матриц сложных четырех­полюсников выполняются только для регулярных соединений, т. е. таких, в которых токи входящие и выходящие в каждой паре зажимов равны.

Мостовой четырехполюсник

При анализе и синтезе пассивных симметричных четырехполюсников широко используются мостовые четырехполюсники. Доказано, что для лю­бого пассивного симметричного четырехполюсника можно найти эквива­лентный мостовой (рис. 6. а).

Мостовой четырехполюсник можно представить как параллельное со­единение двух простых четырехполюсников (рис. 6. б). Уравнения, связы­вающие напряжения и токи на зажимах этих четырехполюсников, имеют вид

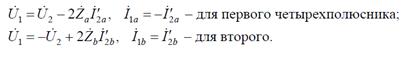
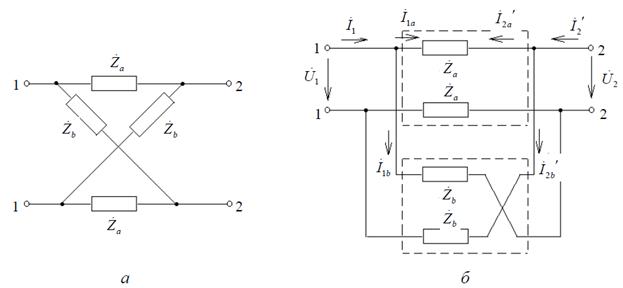
Рисунок 6

С учетом предыдущих выражении, можно получить уравнения для элементарных четырехполюсников

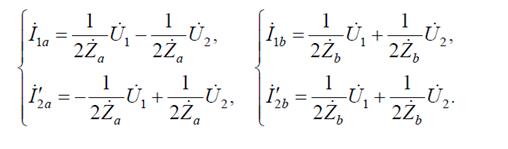
Матрица проводимости мостового четырехполюсника как сумма мат­риц проводимостей имеет вид

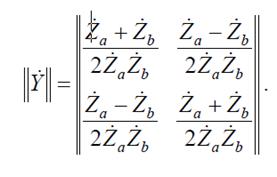
По известным коэффициентам матрицы проводимостей можно найти матрицу А -параметров

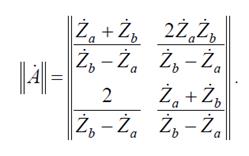
Характеристические параметры симметричного мостового четырехпо­люсника определяются по формулам:

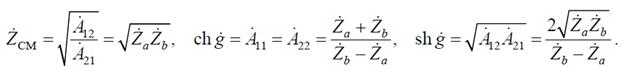
После несложных преобразований получаем

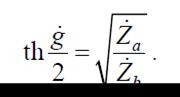
Коэффициент передачи по напряжению мостового четырехполюсника при согласованной нагрузке

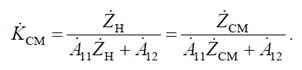
Подставив в эту формулу значения первичных параметров, получим:

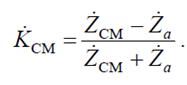
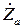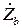Мостовой четырехполюсник обладает интересными свойствами в том случае, когда элементы  и  реактивны и имеют разные знаки. Характе­ристическое сопротивление при этом оказывается вещественным:

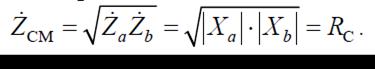
Коэффициент передачи по напряжению реактивного мостового четы­рехполюсника при согласованной нагрузке

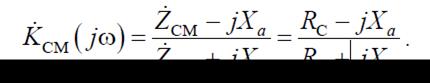
Отсюда видно, что модуль коэффициента передачи 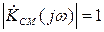 и, значит, такой четырехполюсник пропускает все частоты оез изменения их амплитуд.

Фазовый сдвиг напряжений на входе и выходе определяется из формулы

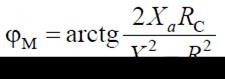
и, следовательно, является функцией частоты. Такие цепи называются четы­рехполюсниками чисто фазового сдвига и используются при синтезе цепей по заданным частотным характеристикам.

---

Дата добавления: 2019-07-15; просмотров: 531; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!