Формування динамічних характеристик електропривода
Динамічні характеристики будь-якої системи регулювання представляють собою реакцію системи на стрибкоподібну зміну задаючого сигналу чи збурення. Стосовно автоматизованого електропривода це буде зміна швидкості двигуна, зумовлена миттєвою зміною задаючої напруги чи моменту сил опору (ударне навантаження), і кількісно буде описуватись диференціальним рівнянням системи регулювання при дії вказаних зовнішніх впливів.
Отже, для формування бажаних динамічних процесів необхідно знати диференціальне рівняння системи і мати засоби зміни коефіцієнтів цього рівняння, щоби в системі протікали процеси, близькі до технічно-оптимальних, тобто таких, коли час перехідного процесу буде мінімально можливим і перерегулювання не перевищить 8%.
Узагальнена системи стабілізації швидкості з сумуючим підсилювачем в усталеному режимі описується системою рівнянь /52/. Щоб описати цю ж систему в динамічних режимах, необхідно ці рівняння доповнити членами, які визначають зміну енергії в її ланках. Тому при зміні задаючої напруги 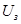 і моменту навантаження
і моменту навантаження 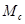 маємо наступну систему рівнянь:
маємо наступну систему рівнянь:
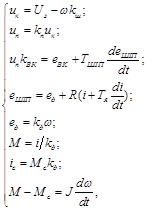 /69/
/69/
де 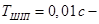 стала часу широтно-імпульсного перетворювача;
стала часу широтно-імпульсного перетворювача;
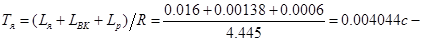
стала часу якорного кола;
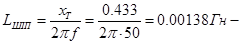
індуктивність трансформатора; 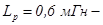 індуктивність згладжуючого реактора;
індуктивність згладжуючого реактора; 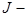 зведений до вала двигуна момент інерції привода.
зведений до вала двигуна момент інерції привода.
Розв’язок системи рівнянь /69/, якою описуються перехідні процеси, матиме вигляд:
|
|
|
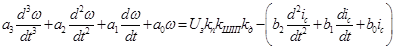 , /70/
, /70/
де
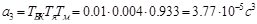 ;
;
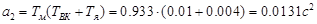 ;
;
 ;
;
 ;
;
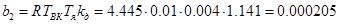 ;
;
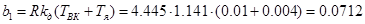 ;
;
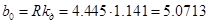 ;
;
 електромеханічна стала часу.
електромеханічна стала часу.
Підставивши числові значення, отримаємо:
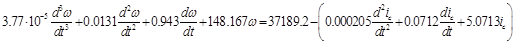
Будь-яка система автоматичного регулювання повинна бути стійкою. Систему, робота якої описуються диференціальним рівнянням ІІІ-го прядку, найбільш просто перевіряти на стійкість за критерієм Рауса-Гурвіца. Згідно з цим критерієм система буде стійкою, якщо коефіцієнти лівої частини рівняння /70/ будуть додатними числами і
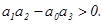 /71/
/71/
Маємо 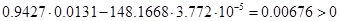 , отже система стійка.
, отже система стійка.
Система стабілізації швидкості повинна бути не тільки стійкою, але і забезпечити бажані перехідні процеси, зокрема, перехідні процеси, викликані зміною задаючої напруги, або зміною моменту Мс, близькими до технічно-оптимальних.
На підставі діаграми Вишеградського доведено, що технічно-оптимальні перехідні процеси в статичній системі будуть тоді, коли коефіцієнти нормованого рівняння системи
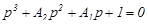 /72/
/72/
будуть такими: 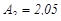 і
і 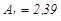 [3, с.287, табл.10.5].
[3, с.287, табл.10.5].
Змінити величини коефіцієнтів при першій і другій похідних за швидкістю можна введенням в контур регулювання похідних за швидкістю і струмом з коефіцієнтами  і
і 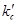 .
.
При подачі на вхід сумуючого підсилювача додатково напруг зв’язків за похідними
|
|
|
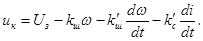 /73/
/73/
Замінивши в системі рівняння /69/ перше рівняння рівнянням /73/, записують нову систему рівнянь, її розв’язують і отримують рівняння, яке буде аналогічним /70/, але з такими коефіцієнтами:
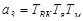 ;
;  ;
;
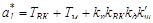 ;
; 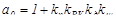 ;
;
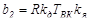 ;
; 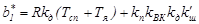 ;
; 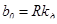 .
.
Коефіцієнтами нормованого рівняння /72/ зв’язані з даними коефіцієнтами такими залежностями:

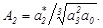 /74/
/74/
Оскільки коефіцієнти 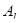 і
і 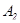 визначені з умови бажаних перехідних процесів, то розрахункові значення коефіцієнтів зв’язків за похідними
визначені з умови бажаних перехідних процесів, то розрахункові значення коефіцієнтів зв’язків за похідними  і
і  знаходять з рівнянь
знаходять з рівнянь
 ;
;
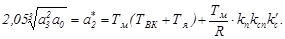 /75/
/75/
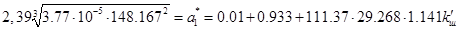 ,
,
звідки 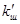 =0.00035
=0.00035
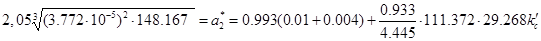 ,
,
Звідки
 =-1,313∙10-6
=-1,313∙10-6
Реалізувати зворотні зв’язки за похідними можна за допомогою реальних диференціюючих ланок.
Дата добавления: 2019-07-15; просмотров: 127; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
