Анализ спектра отклика НЭ на гармоническое воздействие

Методы спектрального анализа

Гармонический анализ отклика НЭ осуществляется при воздействии на него гармониче­ского колебания со «смещением», представляемого выражением:

и ( t )= U ₀ + U _{т 1} cosω₁ t .

Цель гармонического анализа отклика - определение его спектрального состава. При этом имеется ввиду, что НЭ безинерционный. Под таким НЭ подразумевается любой электронный прибор с нелинейной ВАХ при использовании его в диапазоне частот, на которых можно пренебречь влиянием паразитных параметров (внутренних емкостей и индуктивностей).

Наиболее распространенные методы анализа и случаи их использования приведены в таблице 1.

Таблица 1 - Методы спектрального анализа.

Метод спектрального анализа	Способ аппроксимации ВАХ
С использованием тригонометрических формул кратного аргумента (аналитический)	Полиномиальный
Угла отсечки (графический)	Кусочно-линейный
С использованием формул трех и пяти ординат(графоаналитический)	Не требует аппроксимации характеристики НЭ
С использований функций Бесселя от мнимого аргумента	Экспонента или сумма экспонент

Метод кратных аргументов основывается на получении выражения реакции у ( t )путем подстановки в степенной полином, которым представлена нелинейная характеристика у = (х), выражения воздействия х ( t ), представленного в виде ряда Фурье. После элемен­тарных преобразований с учетом известных тригонометрических формул кратных аргу­ментов и группировки слагаемых с одинаковыми аргументами получают выражение от­клика в виде ряда.

При методе угла отсечки используется кусочно-линейная аппроксимация характеристи­ки НЭ. Форма реакции находится графическим методом (методом проекций), который заключается в построении третьей проекции у(t )(реакции НЭ) по известным двум: воз­действию х ( t )и характеристике у = (х). При построении графика у ( t )сначала наносят характерные точки: максимумы, минимумы, пересечения с осью абсцисс, - а затем про­межуточные точки. Спектральный состав реакции определяется при разложении ее в ряд Фурье.

Метод кратных аргументов.

Метод кратных аргументов применяется при слабонелинейном режиме работы НЭ.

Рассмотрим режим работы, при котором напряжение сигнала и ( t )не выходит за пределы точки начала характеристики U_н(рис.3.) и ВАХ удовлетворительно аппроксими­руется степенным полиномом третьей степени:

i (и) = а₀ + а₁(и- U ₀ ) +а₂(и- U ₀ )² + а₃(и- U ₀ )³,

 

где u ( t ) = U ₀ + U_т1 cosω ₁t- входной сигнал.

Подставим в заданный полином выражение входного сигнала:

i ( t ) = а₀ + а₁ U _т1cos ω₁ t + а₂( U _т1cos ω t)²+ а₃( U _т1 cos ω ₁t )³

= а₀ + а₁ U _т1cos ω₁ t + а₂ U _т1 ²cos²ω ₁t+ а₃ U _т1 ³cos³ω ₁t .

Применяя тригонометрические формулы кратных аргументов:

 

cos²α = 1/2 + 1/2cos2α,

cos³α = 3/4cos α + 1/4cos3 α,-

избавимся от степеней тригонометрических функций:

 

i ( t ) =а₀ + а₁ U _т1cos ω₁ t + 1/2 а₂ U _т1 ² + 1/2 а₂ U _т1 ²cos2ω₁t + 3/4 а₃ U _т1 ³cos ω₁t₁+ 1/4 а₃ U _т1 ³cos 3ω₁t₁

Сгруппируем слагаемые с одинаковым аргументом косинуса:

i ( t ) = (а₀ + 1/2 а₂ U _т1 ² ) + (а₁ U _т1 + 3/4 а₃ U _т1 ³ )cosω₁t₁+1/2 а₂ U _т1 ²cos2ω₁t + 1/4 а₃ U _т1 ³cos 3ω₁t_1.

Заменим коэффициенты обозначением тока:

I ₀ =а₀ +1/21/2 а₂ U _т1 ²- постоянная составляющая;

I _т1 = а₁ U _т1 +3/4 а₃ U _т1 ³- амплитуда первой гармоники;

I _{т 2} = 1/2 а₂ U _т1 ²- амплитуда второй гармоники;

I _{т 3} =1/4 а₃ U _т1 ³- амплитуда третьей гармоники.

 

Отклик представим в виде:

i(t) = I ₀ +I _{т 1}cosω t+ I _{т 2}cos2ω t+I _{т 3}cos 3 ω t

 

Представим воздействие и отклик графически  

 

 

 

Рис.7. Спектральные диаграммы гармонического воздействия и отклика на него

 

Выводы:

- спектр отклика при воздействии гармонического сигнала линейчатый;

- частоты составляющих спектра кратны частоте входного сигнала;

- кратность частоты высшей гармоники спектра равна степени полинома;

- постоянная составляющая и четные гармоники определяются только четными степеня­ми напряжения в полиноме;

- нечетные гармоники определяются только нечетными степенями напряжения в поли­номе.

Отметим, что в спектре отклика появились составляющие, отсутствовавшие в спектре входного воздействия. Эти новые составляющие являются результатом реакции нели­нейной цепи и называются нелинейными продуктами, характеризующими нелинейные искажения входного сигнала.

Рассмотренный метод используется при анализе работы усилителей, работающих в не­линейном режиме, т.е. когда допустим уровень нелинейных продуктов выше 10%.

Метод угла отсечки.

Метод угла отсечки применяется присущественно нелинейном режиме работы НЭ.

Рассмотрим режим работы, получаемый при сдвиге рабочей точки U ₀влево и увеличе­нии амплитуды возбуждающего напряжения (рис.4). В данном случае целесооб­разно применить кусочно-линейную аппроксимацию ВАХ:

i =0 при u< и i=S(u-U) при u≥

где S- крутизна линейно возрастающего участка ВАХ,

- координата его начала.

Форму реакции находим графическим методом. Типичное взаимное расположение ВАХ

и сигналов показано на рисунке 8.

 

 

 

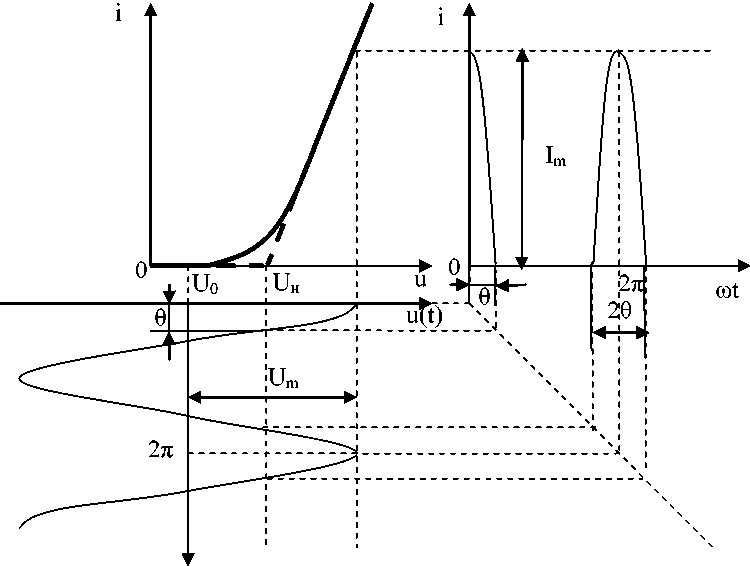
Рис.8. Определение формы реакции методом проекций.

 

Форма реакции имеет вид периодической последовательности косинусоидальных им­пульсов с отсечкой. Полученные импульсы характеризуются двумя параметрами: высо­той 1_ти шириной 2Ɵ .

Угол, соответствующий половине времени существования импульса, называется углом отсечки в. Угол отсечки определяется из равенства:

Ɵ=arccos

 

В соответствии с формулой при заданной ВАХ (фиксированном U_н) угол отсечки Ɵ ре­гулируется выбором амплитуды U _твеличины смещения U ₀ .

Высота (максимальное значение) импульса тока определяется выражением:

I _т = SU _т (1 - cos Ɵ).

Поскольку ток - периодическая функция времени с периодомТ = 2 /ω₁, его можно пред­ставить в виде ряда Фурье:

i(t)= I ₀ + ω₁t₁  + ).

 

Коэффициенты этого ряда являются постоянной составляющей и амплитудами гармоник тока и могут быть вычислены по формулам:

1₀ = а₀ (Ɵ) I _т = SU _т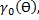

1 _{т п} = а_п (Ɵ)1_т = SU _т

где а_п(Ɵ) −коэффициенты Берга;

= (1 - cos )а_п (Ɵ) −функции Берга.

 

Для ряда значений пкоэффициенты и функции Берга табулированы. Из рассмотрения графиков коэффициентов Берга можно сделать такие заключения: при Ɵ= 0 ток равен нулю (НЭ заперт на протяжении всего периода); при Ɵ=180  отсечка тока отсутствует и режим работы становится линейным; при работе с Ɵ<180  отношение амплитуды первой гармоники к постоянной составляющей больше единицы I _т1 / I ₀ >1 и

растет с уменьшением θ; с повышением номера гармоники максимумы амплитуд гармо­ник перемещаются в область малых значений θ.

Указанные обстоятельства существенно влияют на выбор режима работы НЭ при усиле­нии колебаний, умножении частоты. При умножении частоты для получения наиболь­шей амплитуды нужной гармоники тока (п-ой) необходимо выбрать оптимальное значе­ние угла отсечки:

=120 /п.

Таким образом, вне зависимости от вида аппроксимирующей функции ток через НЭ при гармоническом воздействии представляется суммой постоянной 1₀и гармонических с амплитудами I _т1 , I _т2 , I _т3 , ... и частотами ω₁, 2ω₁, 3ω₁, ..., кратными частоте приложен­ного напряжения, составляющих, т.е. рядом Фурье.

 

---

Дата добавления: 2019-07-15; просмотров: 1653; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!