Параметры аналоговых и цифровых сигналов
Основными параметрами аналоговых сигналов являются:
Длительность сигнала (время передачи) Тс - интервал времени, в течении которого существует сигнал.
Ширина спектра Fc - диапазон частот, в пределах которых сосредоточена основная мощность сигнала.
База сигнала В c - произведение ширины спектра сигнала на его длительность.В c= FcTc
Динамический диапазон Dc - логарифм отношения максимальной мощности сигнала - Pmax к минимальной - Pmin (минимально-различимая на уровне помех):
Dc = 10lg (Pmax/Pmin).
Как правило, основание логарифма определяет единицу измерения (например: десятичный - [Бел], натуральный - [Непер]).
Объем сигнала определяется соотношениемVc = TcFcDc.
Пик-факторомQ-называется отношение его максимальной мощности к средней. В логарифмических единицахQ= 10lg (Pmax/Pср).
Основным параметром цифрового сигнала с точки зрения его передачи является требуемая скорость передачи (бит/с).
Периодические сигналы и их спектры
Периодическим сигналом (током или напряжением) называют такой вид воздействия, когда форма сигнала повторяется через некоторый интервал времени T, который называется периодом. Простейшей формой периодического сигнала является гармонический сигнал или синусоида, которая характеризуется амплитудой, периодом и начальной фазой. (рис.6). Все остальные сигналы будут негармоническими или несинусоидальными. Можно показать, и практика это доказывает, что, если входной сигнал источника питания является периодическим, то и все остальные токи и напряжения в каждой ветви (выходные сигналы) также будут периодическими. При этом формы сигналов в разных ветвях будут отличаться друг от друга.
|
|
|
Рис.6. Гармонический сигнал (синусоида)
Существует общая методика исследования периодических негармонических сигналов (входных воздействий и их реакций) в электрической цепи, которая основана на разложении сигналов в ряд Фурье. Данная методика состоит в том, что всегда можно подобрать ряд гармонических (т.е. синусоидальных) сигналов с такими амплитудами, частотами и начальными фазами, алгебраическая сумма ординат которых в любой момент времени равна ординате исследуемого несинусоидального сигнала. Так, например, напряжение U(рис.7) можно заменить суммой напряжений и, поскольку в любой момент времени имеет место тождественное равенство:
u ( t )= 
Каждое из слагаемых представляет собой синусоиду, частота колебания которой связана с периодом T целочисленными соотношениями.
Для рассматриваемого примера имеем период первой гармоники совпадающим с периодом негармонического сигнала T1=T, а период второй гармоники в два раза меньшим T2=T/2, т.е. мгновенные значения гармоник должны быть записаны в виде:
|
|
|
sinωt= 
t 
sinωt= 
t
Здесь амплитуды колебаний гармоник неравны между собой ( 
), а начальные фазы равны нулю.
Рис.7. Пример сложения первой и второй гармоники
негармонического сигнала
Гармоническая составляющая, период которой равен периоду негармонического сигнала, называется первой или основной гармоникой сигнала. Все остальные составляющие называются высшими гармоническими составляющими. Гармоника, частота которой в k раз больше первой гармоники (а период, соответственно, в k раз меньше), называется k - ой гармоникой. Выделяют также среднее значение функции за период, которое называют нулевой гармоникой. В общем случае ряд Фурье записывают в виде суммы бесконечного числа гармонических составляющих разных частот:
u(t)= 
+ 
)
где k - номер гармоники; ω - угловая частота k - ой гармоники;
ω1=ω=2π/T- угловая частота первой гармоники; - нулевая гармоника.
Для сигналов часто встречающихся форм разложение в ряд Фурье можно найти в специальной литературе. В таблице 1 приведены разложения для восьми форм периодических сигналов. Следует отметить, что приведенные в таблице 1 разложения будут иметь место, если начало системы координат выбраны так, как это указано на рисунках слева; при изменении начала отсчета времени t будут изменяться начальные фазы гармоник, амплитуды гармоник при этом останутся такими же. В зависимости от типа исследуемого сигнала под V следует понимать либо величину, измеряемую в вольтах, если это сигнал напряжения, либо величину, измеряемую в амперах, если это сигнал тока.
|
|
|
Таблица 1
| График f(t) | Ряд Фурье функции f(t) | Примечание |
| 
| k=1,3,5,...
|
| 
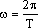
| k=1,3,5,...
|
| 
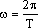
| k=1,3,5,...
|
| 
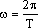
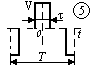
| k=1,2,3,4,5
|
| 
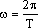
| k=1,3,5,... |
| 
| k=1,2,3,4,5
|
| 
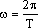
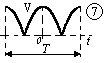
| S=1,2,3,4,..
|
| 
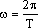
| k=1,2,4,6,...
|
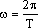
Совокупность всех гармонических составляющих негармонического сигнала называется спектром этого сигнала. Из этого набора гармоник выделяют и различают амплитудный и фазовый спектр. Различают амплитудный и фазовый спектр сигнала:
- амплитудный спектр сигнала — амплитуды всех гармоник, из которых складывается негармонический сигнал
- фазовый спектр сигнала — совокупность начальных фаз всех гармоник
|
|
|
Амплитудный спектр обычно представляют диаграммой в виде набора вертикальных линий, длины которых пропорциональны (в выбранном масштабе) амплитудным значениям гармонических составляющих, а место на горизонтальной оси определяется частотой (номером гармоники) данной составляющей.
Аналогично рассматривают фазовые спектры как совокупность начальных фаз всех гармоник; их также изображают в масштабе в виде набора вертикальных линий.
Следует заметить, что начальные фазы в электротехнике принято измерять в пределах от – 
до + Спектры, состоящие из отдельных линий, называют линейчатыми или дискретными. Спектральные линии находятся на расстоянии f друг от друга, где f - частотный интервал, равный частоте первой гармоники f .Таким образом, дискретные спектры периодических сигналов имеют спектральные составляющие с кратными частотами - f, 2f, 3f, 4f, 5f и т.д.
Для примера найдём амплитудный и фазовый спектр для сигнала однополупериодного выпрямления (см. табл.1 график8), изменяющегося по закону: 
ωt при -T/4<t<T/4; u(t) = 0 при T/4<t<3/4T. Такой сигнал формируется из синусоиды посредством исключения (схемным путем с использованием вентильных элементов) отрицательной части гармонического сигнала.
Ряд для этого сигнала Фурье содержит постоянную составляющую (нулевую гармонику), первую гармонику и далее набор только четных гармоник, амплитуды которых быстро убывают с ростом номера гармоники. Если, например, положить величину V = 100 B, то, умножив каждое слагаемое на общий множитель 2V/π , найдем
Приведем полученное выражение к синусоидальной форме записи слагаемых, используя известные из математики формулы: cos(x) = sin(x+90˚) и
-cos(x) = sin(x-90˚).
Окончательно получим:
31,8+50sin(ωt+ 
) + 21,2sin(2ωt+ ) + 4,25sin(4ωt 
) +
+1,82sin(6ωt+ ) 
…
а) б)
Рис. 8. Линейчатый спектр сигнала однополупериодного выпрямления: а)амплитудный; б)фазовый
В соответствии с теорией рядов Фурье точное равенство негармонического сигнала сумме гармоник имеет место только при бесконечно большом числе гармоник. Расчет гармонических составляющих на ЭВМ позволяет анализировать любое число гармоник, которое определяется целью расчета, точностью и формой негармонического воздействия. Если длительность сигнала t независимо от его формы много меньше периода T, то амплитуды гармоник будут убывать медленно, и для более полного описания сигнала приходится учитывать большое число членов ряда. Эту особенность можно проследить для сигналов, представленных в таблице 1 - 5 и 6, при выполнении условия τ <<T. Если негармонический сигнал по форме близок к синусоиде (например, сигналы 2 и 3 в табл.1), то гармоники убывают быстро, и для точного описания сигнала достаточно ограничиться тремя - пятью гармониками ряда.
Дата добавления: 2019-07-15; просмотров: 2800; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!