Занятие 9. Неоднородные системы линейных алгебраических уравнений
Пример 1. Исследуем неоднородную систему линейных алгебраических уравнений
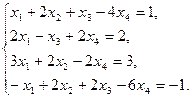
Исследовать неоднородную систему — ответить на вопрос является ли система совместной, и если является, то найти ее общее решение.
Решение. Решим задачу методом Гаусса-Жордана.
Приведем расширенную матрицу системы к ступенчатому виду, выполняя элементарные преобразования строк (прямой ход метода Гаусса):

Ранг расширенной матрицы системы равен рангу матрицы системы и равен двум:
RgAp = RgA= r = 2, система совместна. Число неизвестных n =4, r < n — приведенная однородная система нетривиально совместна.
Кроме того, очевидно, множества решений исходной системы и системы с преобразованной матрицей совпадают.
Продолжим преобразование расширенной матрицы системы, выполняя элементарные операции со строками так, чтобы базисный минор матрицы стал единичным (обратный ход метода Гаусса):
 .
.
Запишем эквивалентную систему уравнений:

Как и в примере 1, переменные  — базисные переменные, а
— базисные переменные, а  — свободные.
— свободные.
Перенесем свободные переменные вправо:

Получили выражение базисных переменных через свободные переменные. Такое выражение — общее решение неоднородной системы, записанное «на языке систем».
Найдем частное решение неоднородной системы. Для этого положим значения свободных переменных равными  и вычислим базисные переменные:
и вычислим базисные переменные:

и тогда вектор  — частное решение неоднородной системы.
— частное решение неоднородной системы.
|
|
|
Приведенная однородная система — система из примера 1.
Воспользуемся решением предыдущего примера:
 ,
, 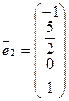 — фундаментальная система приведенной однородной системы,
— фундаментальная система приведенной однородной системы,  — общее решение приведенной однородной системы.
— общее решение приведенной однородной системы.
Тогда 
Проверим:

Верно.
Ответ: Система совместна, ее общее решение 
Задача 9.1. Исследовать совместность и найти общие решения систем:
1)  2)
2)  3)
3)  4)
4) 
4)  5)
5) 
6)  6*)
6*) 
Занятие 10. Контрольная работа по теме «Матрицы. Системы линейных алгебраических уравнений»
Занятие 11. Линейный оператор. Матрица линейного оператора. Преобразование координат вектора и матрицы линейного оператора при изменении базиса
Пример 1.
Пусть A и B — операторы, действующие в R3:
 ,
,  и
и 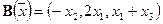 .
.
Найдем  .
.
В качестве дополнительного задания докажем линейность операторов, найдем их матрицы.
Решение
Сначала выполним дополнительное задание.
Докажем линейность оператора A:

 Очевидно, что оба равенства справедливы для произвольных векторов
Очевидно, что оба равенства справедливы для произвольных векторов  и
и  и любого числа
и любого числа  .
.
Докажем линейность оператора B:
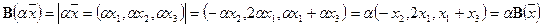
 Очевидно, что оба равенства справедливы для произвольных векторов
Очевидно, что оба равенства справедливы для произвольных векторов  и
и  и любого числа
и любого числа  .
.
Запишем матрицу оператора A:  ,
,
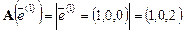 ,
,
|
|
|
 ,
,
 ;
;
запишем координаты образов базисных векторов столбцами — получим матрицу оператора A:
 .
.
Запишем матрицу оператора B:  ,
,
 ,
,
 ,
,
 ;
;
запишем координаты образов базисных векторов столбцами — получим матрицу оператора B:
 .
.
Перейдем к решению самой задачи: найдем 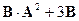 .
.
Первый способ решения задачи
Сначала найдем  :
:  ,
,  ;
;
Затем найдем  :
:  ,
,  теперь найдем
теперь найдем  :
:

и, наконец, найдем 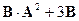 :
:

Получили:
Второй способ решения задачи
Сначала найдем матрицу оператора 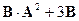 :
:
 ,
,  ,
,

и тогда
 .
.
Сравним с результатом, полученным первым способом:
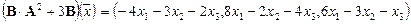 — полное совпадение.
— полное совпадение.
Пример 2. Вектор  задан своими координатами в базисе
задан своими координатами в базисе  . Найдем координаты вектора
. Найдем координаты вектора  в базисе
в базисе 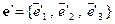 :
: 
Решение. Используем формулу  преобразования координат вектора при изменении базиса. Запишем матрицу перехода от базиса
преобразования координат вектора при изменении базиса. Запишем матрицу перехода от базиса  к базису
к базису  — ее столбцы — координаты векторов
— ее столбцы — координаты векторов  в базисе
в базисе  :
:
 .
.
Найдем обратную матрицу методом Гаусса-Жордана

 и тогда
и тогда  .
.
Проверим: 
Получили заданные в условии координаты вектора в исходном базисе.
Ответ: 
Пример 3. Линейный оператор A, действующий в пространстве R3, задан в в базисе 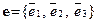 матрицей
матрицей  . Найдем матрицу оператора A, в базисе
. Найдем матрицу оператора A, в базисе  :
: 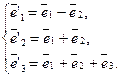
Решение. Используем формулу  преобразования матрицы линейного оператора при изменении базиса. Запишем матрицу перехода от базиса
преобразования матрицы линейного оператора при изменении базиса. Запишем матрицу перехода от базиса  к базису
к базису  и вычислим обратную к ней (см. предыдущий пример):
и вычислим обратную к ней (см. предыдущий пример): 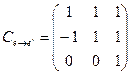 ,
, 
|
|
|
 .
.
Проверим. Проверить можно так: найти образы новых базисных векторов и записать матрицу в новом базисе.
Можно проверить «случайные» арифметические ошибки:
 :
:
 ,
, 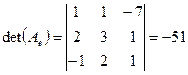 .
.
Ответ: 
Пример 4. Найдем ранг, дефект и базис ядра линейного оператора A, заданного в некотором базисе в R3 матрицей  .
.
Решение. Приведем матрицу оператора к ступенчатому виду:
 .
.
Следовательно, 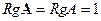 ,
,  .
.
Ядро оператора описывается равенством  .
.
Методом Гаусса получили выражение для общего решения: 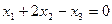 или, что то же самое,
или, что то же самое,  .
.
Найдем ФСР (базис в пространстве решений однородной системы):  .
.
Базис в пространстве решений однородной системы  — это и есть базис в ядре оператора A, заданного в некотором базисе в R3 матрицей A.
— это и есть базис в ядре оператора A, заданного в некотором базисе в R3 матрицей A.
Ответ:  ,
, 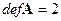 ,
,
базис в ядре оператора образуют векторы  .
.
Задача 11.1. Вектор  задан своими координатами в базисе
задан своими координатами в базисе  . Найти координаты вектора
. Найти координаты вектора 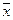 в базисе
в базисе  , где
, где  ,
,  ,
,  .
.
Задача 11.2. Вектор  задан своими координатами в базисе
задан своими координатами в базисе  . Найти координаты вектора
. Найти координаты вектора  в базисе
в базисе  , где
, где  ,
,  ,
,  .
.
Задача 11.3. Линейный оператор, действующий в R3, задан в базисе  . матрицей
. матрицей 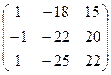 . Найти матрицу оператора в базисе
. Найти матрицу оператора в базисе  , где
, где  ,
,  ,
,  .
.
|
|
|
Задача 11.4. Линейный оператор, действующий в R3, задан в базисе  . матрицей
. матрицей  . Найти матрицу оператора в базисе
. Найти матрицу оператора в базисе  , где
, где  ,
,  ,
,  .
.
Дата добавления: 2019-02-22; просмотров: 331; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
