Занятие 2. Векторное, смешанное произведение векторов

Стр 1 из 5Следующая ⇒

Nbsp; Оглавление Занятие 1. Геометрические векторы. Линейные операции. Скалярное произведение векторов 2 Занятие 2. Векторное, смешанное произведение векторов. 6 Занятие 3. Плоскость и прямая в пространстве. 10 Занятие 4. Контрольная работа по теме «Аналитическая геометрия». 16 Занятие 5. Матрицы. Операции над матрицами. 17 Занятие 6. Определители. Приведение матрицы к ступенчатому виду. Ранг матрицы.. 18 Занятие 7. Обратная матрица. Правило Крамера. 22 Занятие 8. Однородные системы линейных алгебраических уравнений. 25 Занятие 9. Неоднородные системы линейных алгебраических уравнений. 28 Занятие 10. Контрольная работа по теме «Матрицы. Системы линейных алгебраических уравнений» 31 Занятие 11. Линейный оператор. Матрица линейного оператора. Преобразование координат вектора и матрицы линейного оператора при изменении базиса. 32 Занятие 12. Собственные значения и собственные векторы линейного оператора. 38 Занятие 13. Кривые второго порядка. 41 Занятие 14. Поверхности второго порядка. 43 Занятие 15. Контрольная работа по теме «Линейная алгебра». 44

Занятие 1. Геометрические векторы. Линейные операции. Скалярное произведение векторов

Задачи: вычисление длины вектора, деление отрезка в заданном отношении, скалярное произведение векторов, вычисление элементов треугольника.

Определение. Геометрическим вектором называется направленный отрезок.

Обозначаем: , А — начало, B — конец вектора.

Геометрические векторы также обозначают одной буквой: и т.п.

Определение. Длина вектора — расстояние между точками A и B.

Обозначаем: 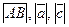и т.п.

Определение. Операции сложения векторов и умножение вектора на число называются линейными операциями с векторами.

Известно (нетрудно доказать), что для линейных операций с векторами справедливо:

;
;
;
;
;
;
;
.

Равенства 1-8 справедливы для произвольных векторов и для любых чисел .

Пример 1. Запись равносильна записи ; .

Пример 2. Пусть , .

Тогда , .

Определение. Трехмерным арифметическим вектором называется упорядоченная совокупность 3 чисел. Обозначается . Числа называются компонентами арифметического вектора.

Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: для любых и и любого числа — ,

Вектор называется нулевым вектором, а вектор — противоположным вектором для вектора .

Определение.Множество трехмерных арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторовR³.

Очевидно, что для любых , , из Rⁿ и любых чисел α, β справедливо:

1. , сложение коммутативно;

2. 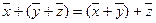,сложение ассоциативно;

3. ;

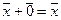4. ;

5. ;

6. , умножение на число дистрибутивно относительно сложения векторов;

7. , умножение на число ассоциативно;

8. 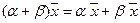, умножение вектора на число дистрибутивно относительно сложения чисел.

Мы видим, что операции сложения и умножения геометрических и трехмерных арифметических векторов имеют одинаковые свойства. Тогда можно проделать такое сопоставление:

Выберем в трехмерном геометрическом пространстве декартову систему координат. Тогда для каждого геометрического вектора однозначно определены координаты : , что означает , причем, как показано выше, .

Это означает, что любой геометрический вектор можно рассматривать как трехмерный арифметический вектор, а пространство геометрических векторов можно изучать как пространство трехмерных арифметических векторов.

Задача. Найти длину медианы треугольника ABC, проведенную из вершины A, если A(1, 0, 2), B(0,1,1), С(3, 0,-2).

Решение. Точка M — середина BC, , .

Тогда .

Ответ. .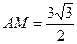

Скалярное произведение векторов

Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначаем: , .

Поскольку 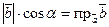и , то

Свойства скалярного произведения. Нетрудно показать, что для произвольных векторов , и , и для любого числа справедливо:

1. ;

2. ;

3. ;

4. 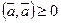, причем тогда и только тогда, когда .

Задача 1(Типовой расчет!). Найти косинус угла между векторами и , если A(1, 2, 0), B(0, 2, -1) и C(0, 0, 1).

Решение. 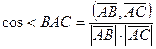; , , — векторы и — ортогональны, угол между ними равен , .

Если не вспомнили признак ортогональности, то можно продолжать вычисления: , , 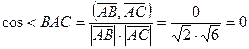. Ответ. .

Задача 2.

Найти все внутренние углы, стороны, площадь, медианы, средние линии и высоты треугольника ABC, если A(1, 1, 0), B(0, 2, –1) и C(0, 1, –1).

Решение. Не будем здесь приводить все вычисления. Найдем 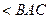, медиану BD, высоту BE и среднюю линию FG.

; , , , , , , , ,

, , ,

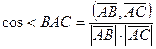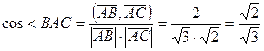D — середина AC — , , .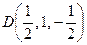

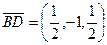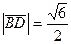Остальные элементы треугольника вычисляются аналогично.

B(0, 2, –1)

Задача 2.1. Доказать, что точки А(3; -1; 2), B(1; 2; -1), C(-1; 1;-3) и D(3; -5; 3) Являются вершинами трапеции. Найти ее стороны и среднюю линию.

*Найти площадь трапеции.

Задача 2.2. Найти орт вектора AB из предыдущей задачи.

Задача 2.3. Даны векторы a = (3; –5; 8) и b = (-1; 1; – 4). Найти:

1) длину суммы и разности векторов a и b; 2) проекцию вектора aна вектор b;

3) проекцию вектора bна вектор a; 4) проекцию суммы векторов a и b на их разность.

Задача 2.4. Векторы a и bобразуют угол 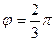, a = |3|, b = |4|. Найти:

1) (a, b); 2) a²; 3) b²; 4) (a + b)²; 5) (2a +3 b, a - b).

Задача 2.5. Даны 2 вектора a = (4; –2; –4) и b = (–6; –3; 2).

Вычислить: 1) (a, b); 2) a²; 3) b²; 4) (a + b)²; 5) (2a +3 b, a - b).

Задача 2.6. Даны вершины треугольника А(3; -1; 2), B(1; 2; -1) и C(-1; 1;-3).

Найти все внутренние и углы треугольника, длины его сторон, площадь, высоту, опущенную из вершины A, медиану, проведенную из вершины A.

Задача 2.7. Доказать, что орты i, j и k попарно ортогональны. Доказать, что любая линейная комбинация ai + b j ортогональна вектору k.

Задача 2.8*. Доказать, что вектор p = b(a,c) – c(a,b)перпендикулярен вектору a.

Задача 2.9*. При каком значении ортогональны векторы a+ b и a– b.

Занятие 2. Векторное, смешанное произведение векторов

До изучения векторного и смешанного произведения векторов, ознакомить студентов с понятиями определители 2-го и 3-го прядка и с правилами их вычисления.

Задачи: вычисление определителя 2-го и третьего порядка, определитель диагональной матрицы, определитель с нулевой строкой (столбцом).

Определители 2-го и 3-го порядка

Определение.Определителем 2-го порядка называется число, вычисленное по квадратной таблице из 4-х чисел следующим образом:

Определение. Определителем 3-го порядка называется число, вычисленное по квадратной таблице из 9-ти чисел следующим образом:

Пример.

Векторное произведение векторов

Задачи: вычисление векторного произведения, вычисление площади параллелограмма, треугольника, векторное произведение коллинеарных векторов, вычисление смешанного произведения, вычисление объема параллелепипеда, тетраэдра, смешанного произведения компланарных векторов.

Определение. Векторным произведением векторов и (обозначаем его 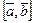) называется вектор, который определяется следующим образом:

o , — угол между векторами и ; (определили длину вектора );

o вектор 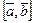ортогонален вектору и вектору ; (определили положение вектора в пространстве);

o векторы , и 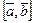образуют правую тройку; (определили направление вектора ).

Правая тройка: из конца вектора 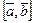поворот от вектора к вектору видится против часовой стрелки. Правую тройку хорошо «моделировать тремя первыми пальцами правой руки.

Важный пример. ,

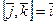Свойства векторного произведения. Нетрудно показать, что для произвольных векторов 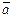, и , и для любого числа справедливо:

1. ;

2. ;

3. ;

4. .

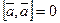Задача 1(Типовой расчет!). Вычислить площадь параллелограмма, построенного на векторах 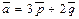и , если — угол между векторами 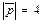и , и .

Решение. S — площадь параллелограмма. 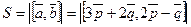. Воспользуемся линейностью векторного произведения (св-ва 2, 3, следствия 1, 2): а поскольку (св-ва 1 и 4) , то имеем

Ответ. .

Смешанное произведение векторов

Определение. Смешанное произведение векторов , и 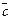(обозначаем его ) определяется равенством 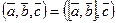, т.е. равно скалярному произведению векторов 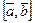и .

Свойства смешанного произведения. Понятно, что свойства смешанного произведения — это свойства скалярного произведения двух векторов, а поскольку первый из сомножителей, , векторное произведение, то получим суперпозицию свойств векторного и скалярного произведений.

Например: .

Рассмотрим только некоторые, наиболее интересные с нашей точки зрения свойства.

Признак компланарности векторов. Векторы, лежащие в одной плоскости (параллельные одной плоскости) называются компланарными векторами.

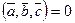тогда и только тогда, когда векторы , и компланарны.

Задача 3(Типовой расчет!). Компланарны ли векторы , , ?

Решение. Вычислим смешанное произведение векторов: .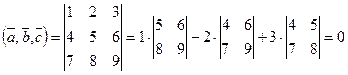

Смешанное произведение векторов равно нулю — векторы компланарны.

Ответ. Векторы компланарны.

Задача 4(Типовой расчет!). Вычислить объем тетраэдра с вершинами в точках A₁(1, -1, 2), A₂(2, 1, 2), A₃(1, 1, 4), A₄(6, -3, 8) и его высоту h, опущенную из вершины A₄.

Решение. Вычислим смешанное произведение векторов , , 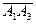и :

Тогда объем тетраэдра . Теперь найдем

высоту тетраэдра h, опущенную из вершины A₄:

, ,

, .

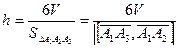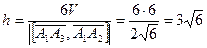Ответ. Объем тетраэдра — 6; высота, опущенная из вершины A₄, — .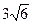

Задача 5(Типовой расчет!). Найти расстояние от точки M₀(1, -1, 2) до плоскости, проходящей через точки M₁(2, 1, 2), M₂(1, 1, 4), M₃(6, -3, 8) .

Решение. Ясно, что искомое расстояние — это длины высоты тетраэдра с вершинами в точках M₀, M₁, M₂, M₃, опущенной из вершины M₀. Следовательно, решение задачи совершенно аналогично решению предыдущей задачи: вычислить объем тетраэдра (смешанное произведение), вычислить площадь основания (половина модуля векторного произведения), вычислить высоту тетраэдра.

Задача 2.10. Векторы a и bобразуют угол , a = |6|, b = |5|.

Найти |[a, b]|.

Задача 2.11. Найти площадь параллелограмма ABCD: А(0; 0; 0), B(1; 1; 0), C(2; 1; 0) и D(1; 0; 0).

Задача 2.12. Даны векторы a = (3; –5; 8) и b = (-1; 1; – 4). Найти:

1) [a+ b, a – b];2) [a+ 3b, a];3) (a, b) [a, b]; 4) [3a+ 4b,2a– b].

Задача 2.13. Даны векторы a = 3i –5j + 8k и b = -i + j – 4k. Найти [a, b].

Задача 2.14*. Найти вектор x, если известно, что он перпендикулярен векторам

a = (2; –3; 1) и b = (1; –2; 3) и x(i + 2j –7k) =10.

Задача 2.15. Векторы a, bи с образуют правую тройку; |a| = 4, |b| = 2, |c| = 3. Вычислить abс.

Задача 2.16. Вектор с перпендикулярен векторам aи b.Угол между векторам aи b равен 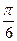. Известно, что |a| = 4, |b| = 2, |c| = 3. Вычислить abс.

Задача 2.17. Проверить компланарность векторов:

1) (2; 3; –1), (1; –1; 3) и (1; 9; – 11);

2) (3; –2; 1), (2; 1; 2) и (3; –1; – 2);

3) (2; –1; 2), (1; 2; –3) и (3; –4; 7);

4) (3; –2; 1), (2; 1; 2) и (1; 9; – 12).

Задача 2.18. Доказать, что точки А(1; 2; –1), B(0; 1; 5), С(–1; 2; 1) и D(2; 1; 3) лежат в одной плоскости.

Задача 2.19. Вычислить объем тетраэдра с вершинами в точках А(1; –2; –1), B(0; 1; 5), С(–1; 2; 1) и D(2; 1; 0).

Дата добавления: 2019-02-22; просмотров: 292; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 Следующая ⇒

Мы поможем в написании ваших работ!