Особенности упругого напряженного состояния горных пород при вдавливании инденторов
При экспериментальном изучении деформирования и разрушения горных пород вдавливанием элементы вооружения породоразрушающих инструментов рассматриваются как инденторы. Они разделены на две большие группы: с плоской рабочей поверхностью (притупленный клин) и со скругленной рабочей поверхностью (зубки с цилиндрической и сферической рабочими поверхностями). Особенности напряженного состояния горных пород при вдавливании элементов вооружения (инденторов) с плоской рабочей поверхностью рассмотрены ниже на примере вдавливания цилиндрического штампа с плоским основанием, а со скругленной рабочей поверхностью – на примере штампа со сферической рабочей поверхностью и клинового штампа с цилиндрической рабочей поверхностью.
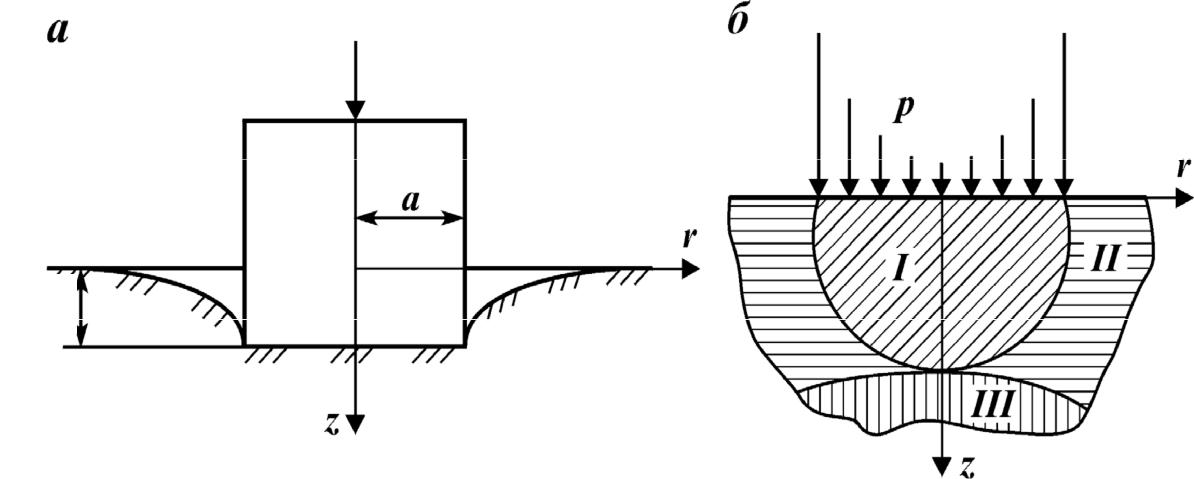
Вдавливание жесткого цилиндрического штампа с плоским основа- нием. Штамп вдавливается в упругое полупространство силойF,действующей по оси z (рис. 4.20 а). Задача осесимметрична, поэтому решение дается в цилиндрических координатах. Распределение давления р по радиусу круга описывается уравнением
| р = | F | , | (4.51) | |||
| 2πа | а2 | − r 2 | ||||
где а – радиус штампа; r – полярный радиус.
F
| h |
Рис. 4.20. Схема испытания (а), распределения давления и области напряженного состояния (б) в горной породе при вдавливании штампа
Из анализа формулы (4.51) видно , что r = 0 , p = F/2πa 2, а если r = a, то р → ∞, т.е. распределение давления по площади контакта весьма неравномерное: минимальное давление действует в центре, а максимальное – на контуре контакта (рис. 4.20 б).
|
|
|
Экспериментальными работами Л. А. Шрейнера и др. установлено, что распределение давлений по плоскости контакта неравномерно только в начальный период вдавливания, а по мере приближения к пределу текучести горной породы давление стремится к равномерно распределенному, т.е. можно принять p = F/πa2.
| Упругий прогиб h у поверхности горной породы под штампом определяет- | |||
| ся по формуле | F(1 − μ 2 | ||
| h у = | ) | (4.52) | |
| 2аЕ | |||
где μ – коэффициент Пуассона; Е – модуль Юнга.
Во все формулы, описывающие вдавливание инденторов, упругие характеристики μ и Е входят в виде комплекса С:
| С = | Е | , | ||
| 1 − μ2 | ||||
который представляет собой модуль деформации (упругости) твердых тел при вдавливании инденторов.
Р.М. Эйгелесом проанализировано напряженное состояние упругого полупространства при вдавливании жесткого штампа. Установлено, что под штампом расположена область I всестороннего сжатия, ограниченная поверхностью σ1 = 0 (рисунок 4.20, б). Размеры этой области определяются радиусом площадки контакта и коэффициентом Пуассона. Область I всестороннего сжатия окружена областью II, где одно из главных напряжений больше нуля (растягивающее).
|
|
|
Область II ограничена снизу поверхностью σ2 = 0. Далее расположена область III , где 
s1 > 0 и s2 > 0.
В качестве основной характеристики напряженного состояния твердого тела при вдавливании приняты максимальные касательные напряжения:
tmax = (s3 – s1)/2.
На рисунке 4.21 приведено распределение максимальных касательных напряжений в деформируемом полупространстве под штампом в относительных величинахtmax / p = f ( z / a ; r / a ) .
Из рисунка 4.21 видно, что линии равных tmax / p замыкаются на контуре штампа, где возникают наибольшие напряжения. Далее зона максимума максимальных касательных напряжений в виде языка уходит вглубь и к оси z. Точки полупространства, прилегающие к контуру штампа, являются особыми, так как при переходе через линию контура давление на поверхность меняется скачком от максимума до нуля (см. рисунок 4.20, б), и образуют первую экстремальную зону, в которой действуют наибольшие касательные напряжения.
На оси симметрии 0z максимальные касательные напряжения tmax / p в начале возрастают и достигают максимума на глубине zm:
|
|
|
,
а затем монотонно уменьшаются по мере увеличения расстояния от поверхности горной породы. Область в окрестности точки с координатами z = zm, r = 0 образует вторую экстремальную зону. На рисунке 4.21 ордината второй экстремальной зоны zm = 0,65a .
Из рисунка видно, что линии равных τmax / p замыкаются на контуре штампа, где возникают наибольшие напряжения. Далее зона максимума максимальных касательных напряжений в виде языка уходит вглубь и к оси z. Точки полупространства, прилегающие к контуру штампа, являются особыми, так как при переходе через линию контура давление на поверхность меняется скачком от максимума до нуля (см. рис. 4.20 б), и образуют первую экстремальную зону, в которой действуют наибольшие касательные напряжения.
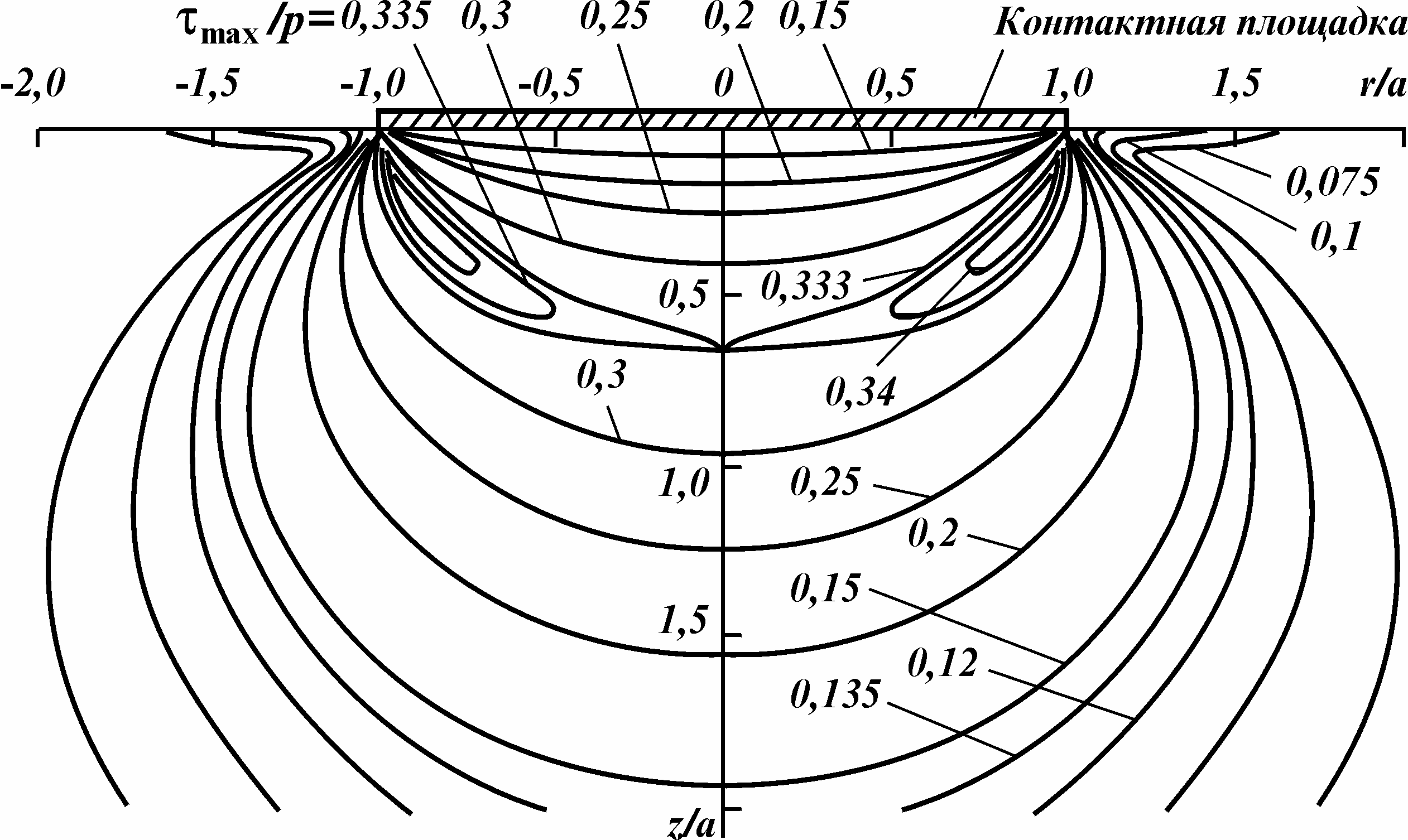
Рис. 4.21. Распределение τmax / p = f (z/a; r/a) в полупространстве под штампом
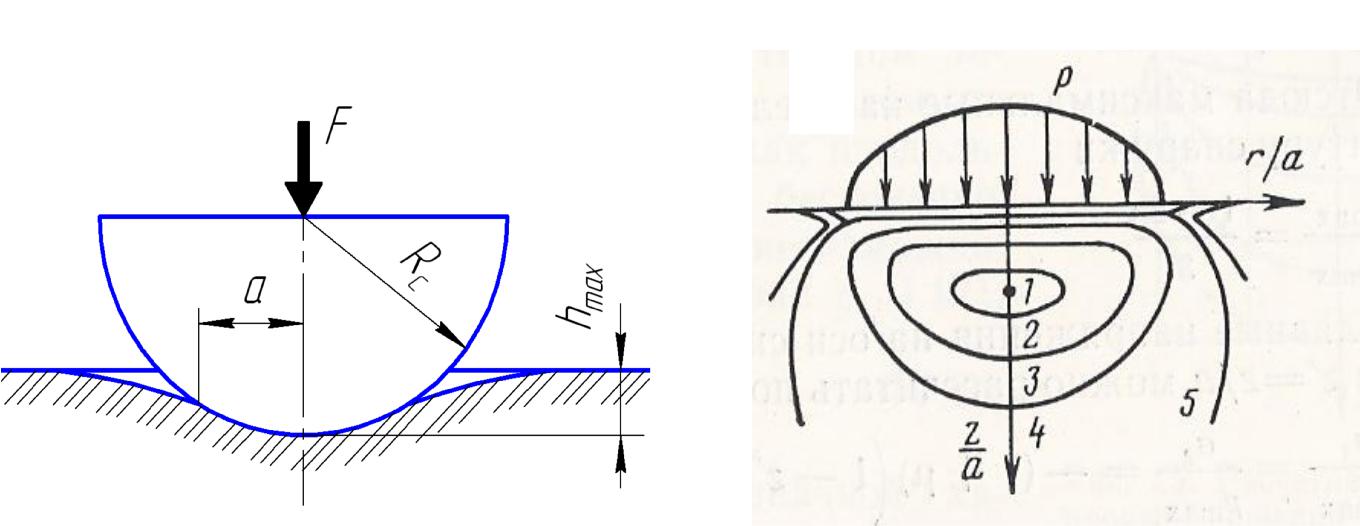
Вдавливание жесткой сферы. Схема вдавливания индентора со сферической рабочей поверхностью приведена на рис. 4.22 а.
а б
Рис. 4.22. Схема вдавливания сферы (а), распределение давления и линии равных значений τmax / pmax под сферой (б): значения τmax pmax: 1 – 0,31; 2 – 0,30; 3 – 0,25; 4 – 0,20; 5 – 0,10
|
|
|
При отсутствии нагрузки сфера контактирует с поверхностью твердого тела в точке. По мере увеличения нагрузки F на сферу формируется круговая площадка контакта радиусом а, который рассчитывается по формуле Герца:
| а = 3 | 3FRс , | (4.53) |
| 4С |
где Rс–радиус сферы; С – модуль деформации(упругости)горной породы привдавливании.
Распределение давления (рис. 4.22 б) по диаметральному сечению площадки контакта описывается уравнением эллипса
р =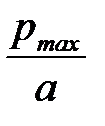 
,
где pmax – максимальное контактное давление в центре площадки
pmax =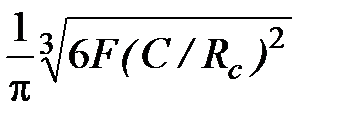 
. (4.54)
Анализ напряженного состояния в твердом теле, проведенный Р.М. Эйгелесом, показал, что структура поля напряжений под сферой такая же, как и под цилиндрическим штампом, но область всестороннего сжатия при вдавливании сферы значительно меньше, чем при вдавливании штампа.
Распределение максимальных касательных напряжений под сферой приведено на рис. 4.22 б, из которого видно, что наибольшее значение максимальных касательных напряжений отмечается на оси симметрии на некоторой глубине от поверхности контакта (около 0,5 а).
Вдавливание индентора с цилиндрической рабочей поверхностью.
Схема вдавливания приведена на рис. 4.23. При отсутствии нагрузки индентор имеет линейный контакт с поверхностью горной породы, касаясь ее своей образующей. По мере увеличения нагрузки появляется и увеличивается площадка контакта шириной 2b. Как правило, ширина формируемой в процессе вдавливания площадки контакта значительно меньше ее длины. Поэтому c целью упрощения аналитического решения задачи Герц принял длину контакта бесконечной. В качестве характеристики нагружения принята равномерно распределенная по длине сила на единицу длины рабочей поверхности индентора F i (интенсивность силы).Решение для половины ширины площадки контактаследующее
b = 2 F i R ц ,
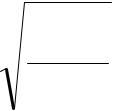πС
где R ц – радиус цилиндрической рабочей поверхности.
Распределение давления по ширине контакта следует эллиптическому закону, как и в случае вдавливания сферы, и рассчитывается по формуле
|
| р max | b2− х2, | |
| b | |||
р =где рmax – максимальное нормальное давление на площадке контакта,
|
| F i С | . | (4.55) |
| πR | |||
| ц |
р max =
В заключение следует подчеркнуть, что величина p max является основной характеристикой нагружения при вдавливании инденторов с криволинейной рабочей поверхностью.
Рис. 4.23. Схема вдавливания индентора с цилиндрической рабочей поверхностью
Дата добавления: 2019-02-22; просмотров: 840; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!