Особенности деформирования и разрушения горных пород в условиях всестороннего сжатия
 а б
а б
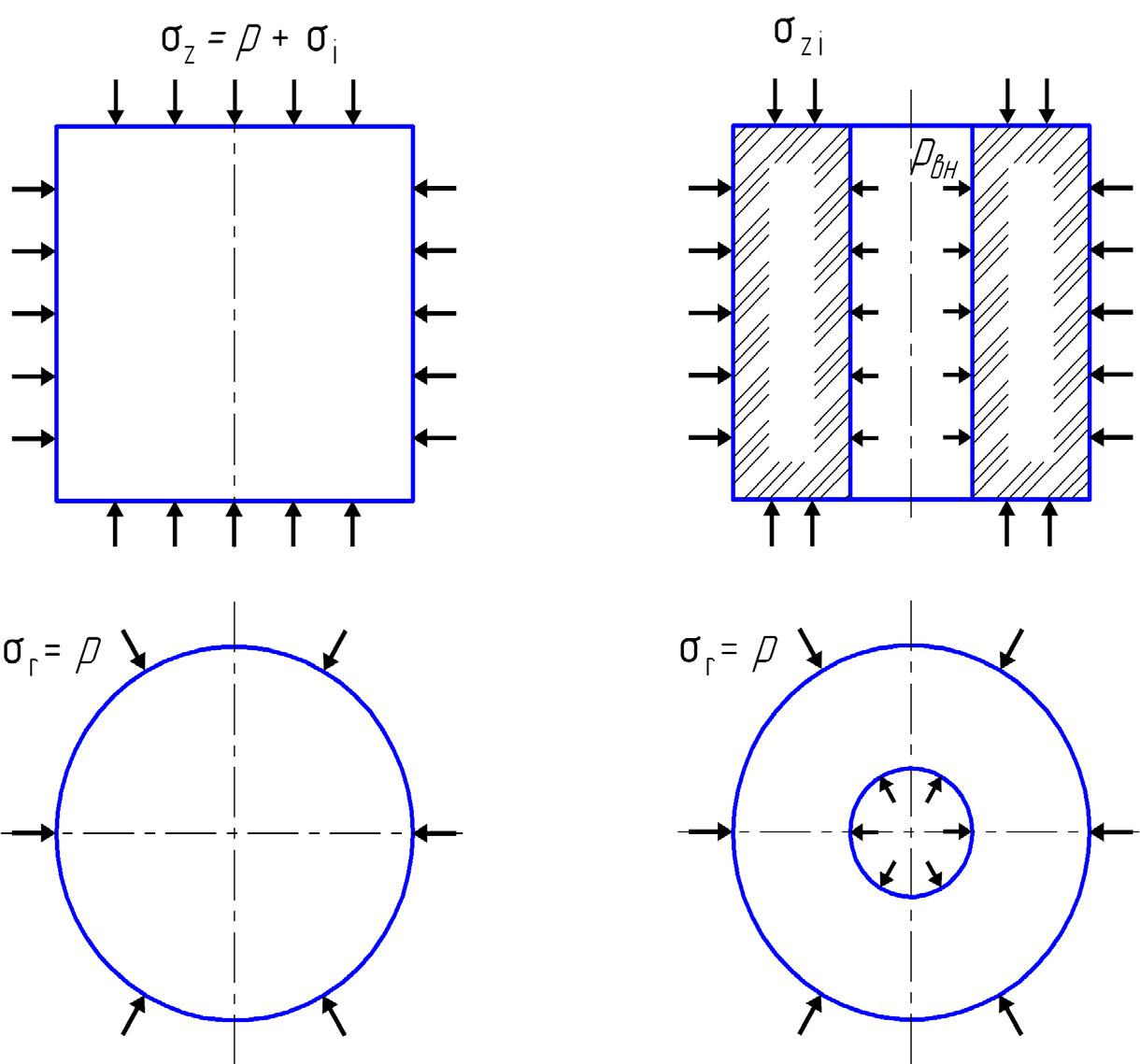
Рис. 4.14. Схемы испытаний горных пород при всестороннем сжатии:
а –схема Кармана; б –схема испытания полого цилиндра
Горные породы в земной коре находятся в условиях всестороннего сжатия в результате действия горного давления. Всестороннее сжатие может быть равномерным, когда
| σ1 = σ2 = σ3, | (4.44) |
и неравномерным, когда хотя бы одно главное напряжение не равно двум другим. В общем случае при неравномерном напряженном состоянии
| σ1 ≠ σ2 ≠ σ3. | (4.45) |
Лабораторные испытания горных пород в условиях всестороннего сжатия выполняют на специальных стендах высокого давления. Применительно к бурению скважин используют две схемы испытаний: схему Кармана и схему испытания полого цилиндра (рис. 4.16).
Схемы испытаний осесимметричные и рассматриваются в цилиндрической системе координат, что упрощает решения аналитических и экспериментальных задач. Например, подстановкой значений компонент напряжений в формулу (4.2) нетрудно показать, что величина приращения Δσz вертикального напряжения при р = const равна интенсивности касательных напряжений σi.
По схеме Кармана испытываются цилиндрические образцы горных пород, аналогичные испытываемым при одноосном сжатии, при разных начальных значениях избыточного давления р. Схема Кармана используется при изучении общих закономерностей деформирования и разрушения горных пород в усло-виях всестороннего сжатия. Схема полых цилиндров используется при модели-ровании этих процессов в горных породах стенки скважины.
Рассмотрим порядок проведения опытов на примере схемы Кармана. Предварительно нагруженный давлением р образец нагревается до заданной температуры и выдерживается в течение суток. Затем проводится нагружение образца до его разрушения. В процессе нагружения увеличивается только вертикальное напряжение σz:
σz = σ3 = р + Δσz = р + σi,
где Δσz – приращение напряжения, равное интенсивности касательных
напряжений σi. Радиальные напряжения в опыте остаются постоянными:
σ1 = σ2 = р.
В процессе испытания ведется запись зависимости величины вертикаль-ной нагрузки от величины изменения длины образца. Полученные зависимости перестраиваются в координатах σi от ε, где ε – вертикальная деформация образца. Характерные графики зависимостей σi от ε, полученные при разных значениях начального давления р (р1 < р2 < р3 < р4) на образцах одной и той же горной породы, приведены на рис. 4.17 а.

Рис. 4.17. Зависимости σ i от ε (а) при испытаниях в условиях всестороннего сжатия и соответствующая зависимость σ iс от σ 0 (б)
Отрезок 0 а1 соответствует одноосному сжатию, т.е. величина р1 была рана атмосферному давлению. В точках а1, а2, а3 и а4 был достигнут предел текучести образцов породы σis. На отрезках 0 а1, 0а2, 0а3 и 0а4 соблюдался закон Гука (упругое деформирование), на отрезках кривых a2b2, a3b3, a4b4 либо имело место нелинейное пластическое деформирование, которое заканчивалось хрупким разрушением, либо наблюдалась пластическая деформация с разупрочнением (отрезок b2с2), либо пластическим течением (отрезок b3с3) с последующим раз-рушением, либо пластической деформацией с упрочнением (отрезок b4с4). Последнее заканчивалось переходной нелинейной деформацией (отрезок c4d4) и далее разрушением (точка f4). Максимальные значения σi соответствуют пре-делу прочности горной породы σiс в конкретных условиях испытания. При атмосферном давлении σis = σs, а σiс = σсж, т.е. равны пределу текучести и пределу прочности породы при одноосном сжатии. Расчетом может быть определено среднее нормальное напряжение σ0:
| σ0 = р + σis /3. | (4.46) |
Конкретные значения величин σis и σi с по данным Л. А. Шрейнера приведены в табл. 4.3. Величина всестороннего сжатия соответствовала глубине за-легания пород около 4000 м. Из табл. 4.4 видно, что предел текучести каменной соли вырос незначительно, тогда как предел прочности горных пород, в том числе и каменной соли, увеличился в 3-4 раза.
| Результаты испытаний горных пород | Таблица 4.4 | ||
| в условиях всестороннего сжатия | |||
| Горная порода | р,МПа | σis, МПа | σiс, МПа |
| Каменная соль | 0 | – | 26 |
| 90 | 36 | 115 | |
| Доломит | 0 | – | 102 |
| 98 | – | 358 | |
| Песчаник | 0 | – | 53 |
| 97 | – | 232 | |
Получаемые при испытаниях данные позволяют построить предельные зависимости σis от σ0 и σiс от σ0 (паспорт прочности породы) в соответствии с обобщенным условием прочности Мора и теории прочности Мора–Кулона.
Построение зависимости σis от σ0 (паспорта прочности по обобщенному условию прочности Мора).Для каждого опыта определить величинуσis.
По формуле (4.46) рассчитать соответствующие значения σ0. Полученные зна-чения нанести на график (рис. 4.17 б). По найденным точкам рассчитать уравнение регрессии σ0 на σis и построить график зависимости σis от σ0, как показа-но на рисунке 4.17 б, который является графическим изображением паспорта прочности породы, а уравнение регрессии – его аналитическим выражением.
Построение зависимости τs от σср ( паспорта прочности по теории прочности Мора–Кулона).Из рис. 4.16аследует,что в момент достижения предельного состояния
σ1 = σ2 = р;
| Тогда | σ3 | = р + σis. | ||||||
| σ 3 − σ 1 | ( р + σis ) − p | =σis ; | ||||||
| τмах | = | = | (4.47) | |||||
| 2 | 2 | 2 | ||||||
| σср = | σ 3 + σ 1 | = | ( р + σis ) + p | = | σis + p . | (4.48) | ||
| 2 | 2 | 2 | ||||||
Для каждого опыта по формулам (4.47) и (4.48) рассчитать пары значений τмах и σ ср, нанести их на график, рассчитать уравнение регрессии σср на τмах и провести линию графика зависимости τмах от σср, как показано на рис. 4.18.
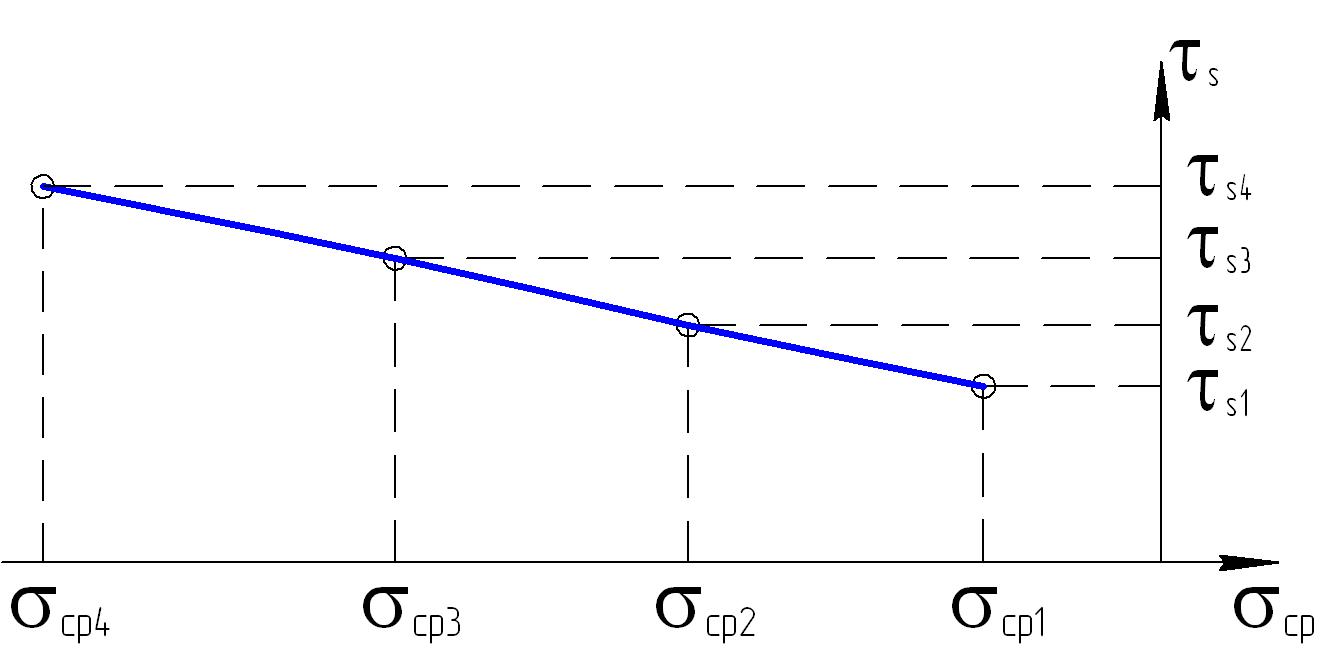
Рис. 4.18. Построение паспорта прочности горной породы по теории прочности Мора–Кулона
В результате:
1) с ростом величины всестороннего сжатия увеличиваются значения предела текучести и предела прочности горной породы;
2) хрупкая горная порода в атмосферных условиях становится пластично-хрупкой в условиях всестороннего сжатия, причем пластичность растет с увеличением всестороннего сжатия;
3) графики зависимостей предельных напряжений от средних нормальных напряжений в горной породе представляют собой монотонно возрастаю-щие прямые или выпуклые кривые линии.
Дата добавления: 2019-02-22; просмотров: 964; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
