Виды разрушения твердых тел. Классы твердых тел

⇐ ПредыдущаяСтр 10 из 97Следующая ⇒

Разрушение называется хрупким, если необратимая (пластическая) деформация, предшествующая разрушению, практически отсутствует, но четко выражены поверхности разрушения. Разрыв – второй вид разрушения, при котором отсутствует поверхность разрушения, например, в результате пластической деформации растяжения сечение твердого тела уменьшается до исчезающе малых размеров. Хрупкое разрушение и разрыв являются предельными видами разрушения.

Пластическое разрушение–это промежуточный вид,который характеризуется значительной пластической деформацией, предшествующей разрушению, и явно выраженной поверхностью разрушения.

В зависимости от ориентации поверхностей разрушения относительно главных напряжений выделяют два вида разрушений:

1) разрушение отрывом, при котором поверхность разрушения перпендикулярна первому главному нормальному напряжению σ₁, при этом необходимо, чтобы хотя бы эта компонента главных напряжений была растягивающей;

2) разрушение срезом (сдвигом) – поверхность разрушения совпадает с поверхностью действия одного из главных касательных напряжений.

Л. А. Шрейнер на основании изучения деформирования и разрушения твердых тел применительно к горным породам выделил три класса по характеру деформирования до разрушения.

На рис. 4.6 приведены характерные зависимости касательных напряжений τ от деформаций сдвига γ для различных классов твердых тел.

а б в

Рис. 4.4. Зависимости τ от γ для хрупких (а), пластично-хрупких (б) и пластичных твердых тел

Хрупкие твердые тела отнесены к первому классу(см.рис. 4.6а).Онидеформируются линейно до момента их разрушения. На графиках зависимости τ от γ выделяется только одна область I упругого деформирования. Прочность твердого тела характеризуется величиной τс, называемой пределом прочности. Хрупко-пластичные твердые тела отнесены ко второму классу(см.рис. 4.6 б). Графики их деформирования содержат две (I и II) или три (I, II и III ) области. Вторая область характеризуется пластическим деформированием при увеличивающемся напряжении ( упрочнении). Третья область характеризуется пластическим деформированием при уменьшающемся напряжении (разупрочнении). Говорят, что имеет место разупрочнение материала. Прочность твердо-

го тела в этом случае описывают двумя показателями: пределом прочности τ_си пределом текучести τ_s.

Пластичные твердые тела(см.рис. 4.6в)деформируются сначала упруго(I область), затем пластически (II область), а разрушение не происходит. Такие горные породы отнесены к третьему классу, и их прочность характеризуется только пределом текучести τ_s.

Теории прочности, применяемые при расчете разрушения горных пород

Прочностные расчеты при проектировании технологии бурения выполняются для стенок скважин с целью предупреждения их пластического деформирования и разрушения и для забоя скважины с целью обеспечения разрушения горной породы породоразрушающими инструментами.

Расчеты выполняются с использованием двух теорий прочности: теории прочности Мора–Кулона и обобщенного условия прочности Мора.

Теория прочности Мора–Кулона.В основе теории лежит гипотеза Морао зависимости предельных касательных напряжений от среднего нормального напряжения и гипотеза Кулона о том, что названная зависимость обусловлена внутренним трением в твердом теле.

Рассмотрим испытание образца твердого тела при сжатии. Схема испытания приведена на рисунке 4.7.

Под действием силы F при достижении предельного состояния формируются поверхности сдвига 1 (показаны пунктиром на рис. 4.7 а), по которым при дальнейшем увеличении нагрузки произойдет разрушение образца. Отбросим верхнюю часть образца и его действие на нижнюю часть заменим нормальным напряжением σN и касательным τп (рис. 4.7 б). Индекс «п» означает, что образец твердого тела находится в предельном состоянии.

Рис. 4.7. Схема разрушения твердого тела при сжатии:

1 –образец; 2 –поверхность разрушения

Предельной характеристикой материала твердого тела по теории прочности Мора–Кулона является зависимость τп от σN. Для определения этой зависимости проводится ряд независимых испытаний, например:

1) растяжение σ₁ = σ_п > 0, σ₂ = σ₃= 0;

2)	сдвиг σ₂ = –σ₃ = σ_п, σ₂ = 0;
3)	сжатие σ₁ = σ₂ = 0, σ₃ = σ_п < 0.	от			по результатам
	При графическом определении зависимости τ_п			σ_N
испытаний строятся соответствующие круги Мора		1,		2 и	3,как показано
на рис. 4.8. Огибающая 4 к кругам Мора является графическим изображением зависимости τ_п от σ_N. На рис. 4.8 представлен случай			линейной зависимости
τ_п от σ_N, которая описывается уравнением
τ_п = τ_с0 + σ_N ⋅ tgϕ,			(4.18)

где τ_c0 – коэффициент сцепления, соответствующий величине предельного ка-сательного напряжения при σ_N = 0; ϕ – угол внутреннего трения.

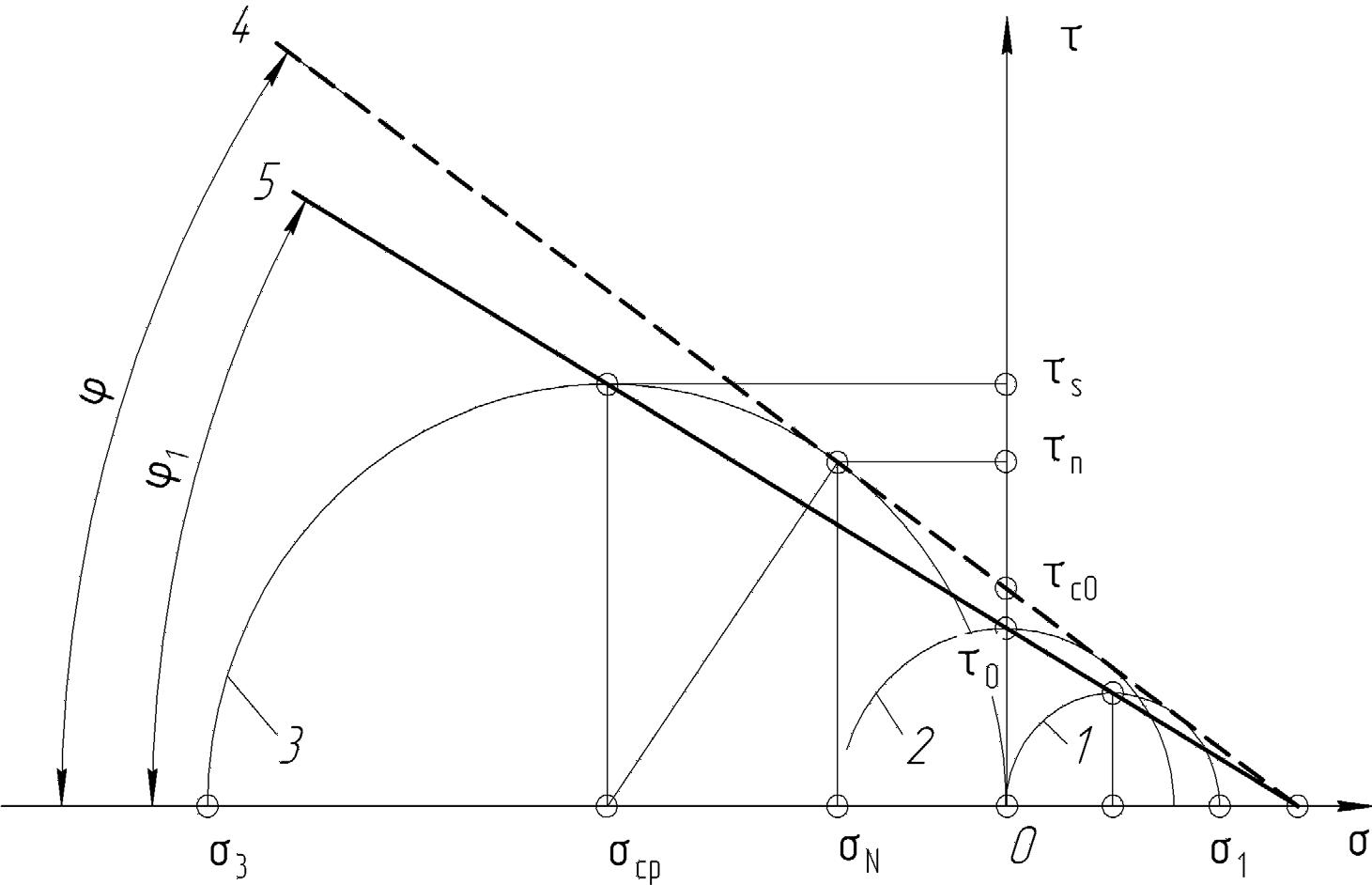
Рис. 4.8. Круги Мора при растяжении (1), сдвиге (2), сжатии (3) и предельные зависимости τ _п от σ _N (4) и τ _s от σ _ср (5)

Рассмотрим координаты т. М, соответствующей испытанию на одноосное сжатие. Величина нормального напряжения σ_N равна

σ_N = σ_ср – ₂tgϕ, (4.19)

где s_{ср -} среднее нормальное напряжение, равное

; (4.20)

t₂ – второе главное ( максимальное) касательное напряжение:

(4.21)

где τ_s – предел текучести материала образца твердого тела.

Величина предельного касательного напряжения t_п равна

t_п . (4.22)

При применении теории прочности Мора–Кулона для ожидаемой по-верхности сдвига следует определить действующие (расчетные) σ_Nр и _р путем подстановки в формулы (4.19) и (4.22) расчетных значений σ_1р и σ_3р.

Далее, подставив в формулу (4.8) σ_N = σ_Nр, определить _п, сопоставить полученное значение _п с _р. и принять решение:

если _п > _р – твердое тело находится в упругом состоянии;

если _п < _р – твердое тело может деформироваться пластически или разрушиться;

при _п > _р делением _п на _р определить запас прочности.

Расчеты с использованием тригонометрических функций угла внутреннего трения целесообразно проводить при известной ориентации поверхностей сдвига. В случае же, когда ориентация не известна или не имеет значения, расчеты могут быть упрощены и проведены непосредственно относительно величин максимальных касательных напряжений и предела текучести материала твердого тела _{s .} В этом случае применяется упрощенная предельная зависимость s от σср, построенная по точкам с координатами, определяемыми по формулам (4.20) и (4.21) (прямая 5 на рис. 4.8).

Линейная зависимость _s от σ_ср имеет вид
_s = _o + Aσ_c_р,	(4.23)

где _o – начальная ордината, равная предельному сопротивлению сдвигу;

А –угловой коэффициент А = tg 1.

Зависимость (4.23) не имеет такой строгий физический смысл, как зависимость (4.18), но упрощает расчеты.

		(4.23) по расчетным данным σ_1р и σ_3р
При применении	зависимости
в опасном сечении твердого тела определяются расчетные значения

и предел текучести материала _s по формуле (4.23), в которую подставляется σ_ср = σ _ср.р. Далее сравниваются непосредственно полученные значения _s

и _max.р и принимается решение.
Параметры зависимостей (4.18) и (4.23) функционально связаны между
собой:
₁ = arctg (sin );	( 4.24)
_о= _с0соs .	(4.25)

Следовательно, зависимости (4.18) и (4.23) при необходимости могут быть получены одна из другой. В случае, когда _n, и _s не зависят от соответст-вующих нормальных напряжений, т.е. = 1 = 0, теория прочности совпадает с теорией максимальных касательных напряжений. Другими словами, третья классическая теория прочности является частным случаем теории прочности Мора–Кулона.

Теория прочности Мора–Кулона широко используется в строительстве и в горном деле применительно к рыхлым несвязным и связным горным породам (грунтам), а также применительно к обломочным сцементированным горным породам, для которых зависимости (4.18) и (4.23) линейные. Причем для рыхлых горных пород

_с0= ₀ = 0.

Для кристаллических горных и для некоторых обломочных горных пород зависимости (4.18) и (4.23) нелинейные выпуклые, что создает некоторые трудности.

При практическом использовании нелинейные зависимости _n от σ_N или s от σср в расчетном диапазоне изменения σN или σср заменяются условными линейными зависимостями. При этом ошибка расчета не выходит за пределы ошибки, получаемой при прочностных испытаниях горных пород.

Обобщенное условие прочности Мора в отличие от теории Мора–Кулона учитывает все три главные напряжения, и предельная характеристика породы определяется как зависимость

σ_iп = f (σ_о),

(4.26)

где σiп – предельная интенсивность касательных напряжений, определяемая по формуле по величинам главных нормальных напряжений в момент достижения в твердом теле предельного состояния:

(4.27)

σ_о – среднее напряжение, рассчитываемое по формуле (4.3).
Зависимость (4.26)	определяется экспериментально путем проведения ря-
да независимых испытаний. Если σ_iп не зависит от		σ_о, то обобщенное условие

прочности Мора совпадает с четвертой (энергетической) теорией прочности. Следовательно, четвертая теория прочности – частный случай обобщенного условия прочности Мора.

Общими принципами расчетов с использованием теорий прочности являются следующие. Для сохранения твердого тела в упругом состоянии необходимо выполнить условие _max ≤ _s или σ_{i max} ≤ σ _is ; _max и σ_{i max} определяются по расчетным напряжением, действующим в опасном сечении

твердого тела в рабочих условиях;

_s = f (σ_cр) или

σ _is = f (σ_о) – определяются

по формулам или графикам предельных зависимостей (4.23) или (4.26),

в которых _п = _s и σ_iп = σ_is – пределы текучести материалов, определенные в стандартных условиях, а аргументы σ_cр или σ_о определяются по тем же расчетным напряжениям, что и величины max или σi max.

Для обеспечения разрушения твердого тела необходимо выполнить условия _max > _с или σ_{i max} > σ_ic , в которых _п, = _с и σ_iп = σ_iс – пределы прочно-сти материалов, определенные в стандартных условиях, а аргументы σcр или σо определяются по расчетным напряжениям, действующим в опасном сечении (области) твердого тела в рабочих условиях.

Экспериментальная проверка показала, что теория прочности Мора– Кулона в случае осесимметричных задач лучше согласуется с экспериментальными данными, чем обобщенное условие прочности Мора.

Дата добавления: 2019-02-22; просмотров: 949; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Мы поможем в написании ваших работ!