Модели пористых осадочных горных пород. Уплотнение пород
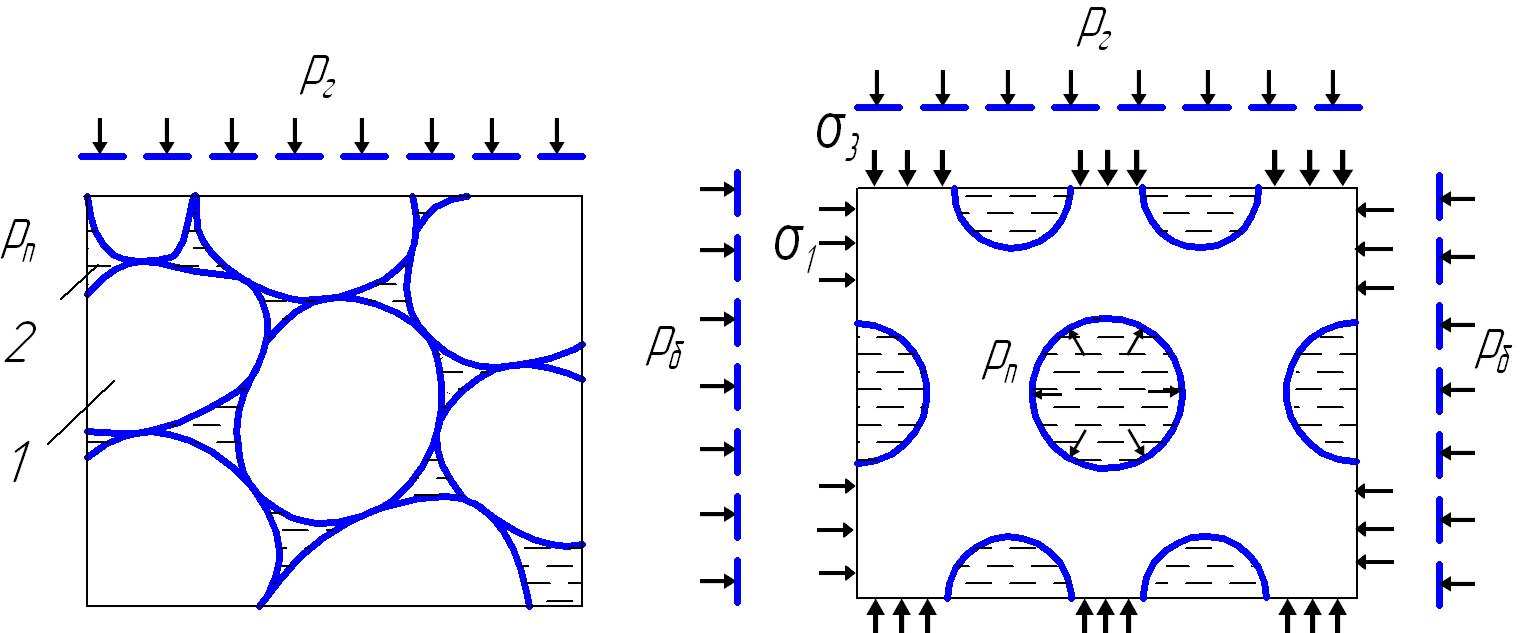
Осадочные горные породы – это двухкомпонентные системы, состоящие из скелета горной породы (твердая часть) и пластового флюида в порах породы. В механике грунтов горные породы рассматриваются как зернистые системы, погруженные в жидкость (рис. 4.12 а).
а б
Рис. 4.12. Схемы зернистой (а) и дырчатой (б) моделей горной породы
Зернистая модель характерна для обломочных несцементированныхгорных пород с точечным контактом обломков друг с другом. Обломки гор-ной породы 1 находятся во флюиде 2 и теряют часть своего веса в соответствии с законом Архимеда. Поэтому для зернистой модели горной породы введено понятие об эффективных напряжениях, равных разности между горным давлением, как в сплошной среде, и пластовым или поровым давлением:
| р эф = р г – р п . | (4.35) |
Действие закона Архимеда возможно, если имеет место как горизонтальная, так и вертикальная проницаемость горных пород на всю глубину. При бурении такие условия выполняются только для поверхностных отложений.
Горные породы представлены как проницаемыми, так и непроницаемыми отложениями. С увеличением глубины уменьшается пористость горных пород, обломочные, особенно глинистые горные породы уплотняются, растет степень их сцементированности. Поэтому допущение о точечном контакте обломков пород с увеличением глубины становится неприемлемым.
|
|
|
Дырчатая модель пористой горной породы(рис. 4.12б).Согласноэтой модели неструктурные элементы горной породы погружены во флюиды, а флюиды находятся внутри горной породы.
Напряжения в скелете горной породы.На выделенный элемент горнойпороды действует геостатическое давление. Если бы все рг воспринималось скелетом породы, то напряжение σ3 было бы максимальным:
| σ3мах = р г /с, | (4.36) |
где с – доля единичной площади, занятая скелетом в рассматриваемом сече-нии. Однако флюид, находящийся в порах, воспринимает на себя часть давления, равного р п(1 – с). Следовательно, вертикальные напряжения σ3 в скелете
| σ3 = | р г − р п (1− с) | = σmax – | р п (1− с) | = | р п + | р г − р п | . | (4.37) | ||
|
| ||||||||||
| с | с | с | ||||||||
| Из формулы | (4.37) следует, что по мере увеличения пластового давления | |||||||||
| наблюдается уменьшение вертикальных напряжений в скелете. Если | рп= рг, | |||||||||
| то σ3 = рг . |
| |||||||||
| Нетрудно показать, что для дырчатой модели горизонтальные напряжения | ||||||||||
| σ1 в скелете равны |
| |||||||||
| σ1 = λр г + р п(1 – с)(1 – λ). | (4.38) | |||||||||
|
|
|
Величины рг и рб как компоненты горного давления характеризуют естественные напряжения в горной породе так, как если бы она была монолитной, а величины σ1 и σ3 – естественные напряжения в скелете модели пористой горной породы.
Очевидно, что доля скелета должна существенно зависеть от пористости горной породы. Для установления вида зависимости доли скелета от пористости в расчетном сечении авторами были проанализированы результаты испытаний горных пород на гидроразрыв, на основании которых для песчано-глинистых пород предложена следующая формула:
| c = exp (–19,16 m2), | (4.39) |
где m – пористость горной породы в долях единицы.
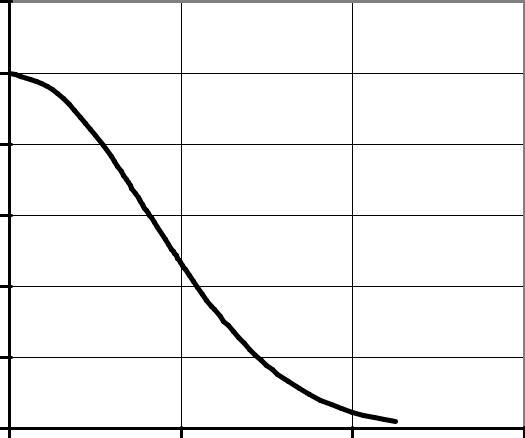
График зависимости (4.39) приведен на рис. 4.13, из которого видно, что при нулевой пористости с = 1, а при увеличении пористости доля скелета быстро уменьшается и асимптотически приближается к нулю.
| 1,2 | |||
| 1,0 | ||||
| скелета | 0,8 | |||
| 0,6 | ||||
| Доля | 0,4 | |||
| 0,2 | ||||
| 0,0 | ||||
| 0 | 0,2 | 0,4 | 0,6 |
Рис. 4.13 Зависимость с от т в расчетном сечении горной породы
|
|
|
Уплотнение пород по мере увеличения глубины их залегания характерно для всех подгрупп горных пород. Но особенно оно велико у глинистых горных пород. По мере уплотнения снижается пористость пород и растет их плотность. В качестве иллюстрации этого явления на рис. 4.14 приведены данные Ю. А. Мельникова.
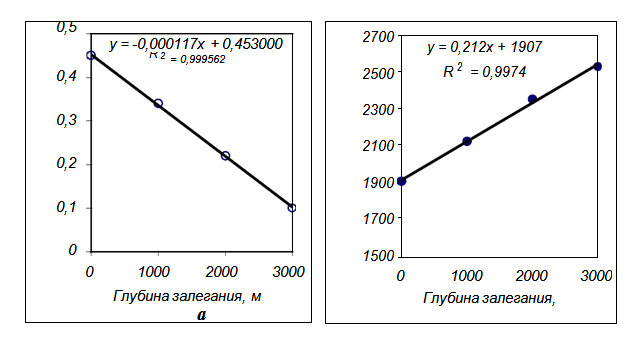
Рис. 4.14. Зависимости пористости (а) и плотности (б) глин от глубины их залегания в Притеречном прогибе
Из рисунка видно, что по мере увеличения глубины залегания пористость глин монотонно уменьшается (в рассматриваем случае в 4,5 раза), а плотность глины растет. Уравнения регрессии глубины залегания на названные показатели приведены на самих графиках. Такое уплотнение является нормальным и характерно для случаев,когда пластовое давление изменяется мо-нотонно. Наличие в отдельных пластах аномального пластового давления приводит к нарушению этих закономерностей. Например, при АВПД степень уплотнения горной породы будет существенно ниже, чем при нормальном давлении. Это явление используется на практике для прогнозирования АВПД в ниже лежащих пористых проницаемых горных породах, вскрытие которых скважиной без обеспечения соответствующего противодавления со ее стороны может привести к притоку в скважину пластового флюида и даже к ее открытому фонтанированию.
|
|
|
Дата добавления: 2019-02-22; просмотров: 793; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
