РЕШЕНИЕ ПРИМЕРНОГО ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ
Задача 1. По каналу связи передаются три сообщения. Вероятность того, что первое сообщение будет искажено равна 0,1, второе – 0,2, третье – 0,3. Найти вероятности следующих событий: 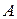 – все три сообщения переданы без искажения;
– все три сообщения переданы без искажения; 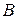 – ровно одно сообщение передано без искажения;
– ровно одно сообщение передано без искажения; 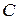 – хотя бы одно сообщение искажено.
– хотя бы одно сообщение искажено.
Решение.
Введем в рассмотрение вспомогательные события 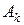 – k-ое сообщение передано без искажений,
– k-ое сообщение передано без искажений, 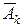 – k-ое сообщение искажено,
– k-ое сообщение искажено, 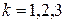 . Согласно условию
. Согласно условию 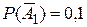 , тогда
, тогда 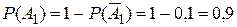 . Аналогично,
. Аналогично, 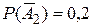 и
и 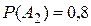 ,
, 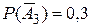 и
и 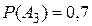 .
.
Так как событие 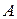 можно представить в виде
можно представить в виде  и события
и события 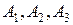 независимы, то вероятность события
независимы, то вероятность события 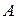 можно найти по теореме умножения вероятностей для независимых событий:
можно найти по теореме умножения вероятностей для независимых событий:

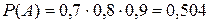 .
.
Событие 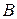 можно представить следующим образом:
можно представить следующим образом:
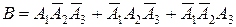 ,
,
причем слагаемые  ,
, 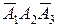 и
и 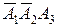 являются попарно несовместными событиями. Поэтому на основании теоремы сложения вероятностей (1) получаем:
являются попарно несовместными событиями. Поэтому на основании теоремы сложения вероятностей (1) получаем:
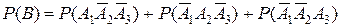 .
.
Для вычисления вероятностей событий 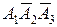 ,
,  и
и 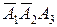 используем теорему умножения вероятностей:
используем теорему умножения вероятностей:
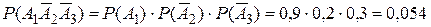 ;
;
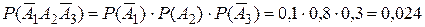 ;
;
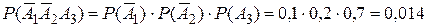 .
.
Таким образом, окончательно получаем:
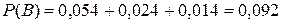 .
.
События  и
и 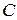 являются противоположными, следовательно,
являются противоположными, следовательно,
 .
.
Ответы: 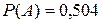 ,
, 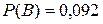 ,
,  .
.
Задача 2. Стрелок ведет стрельбу по цели с вероятностью попадания при каждом выстреле 0,4. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Составить закон распределения случайной величины 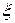 – числа очков, полученных стрелком за 3 выстрела, построить многоугольник распределения, вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
– числа очков, полученных стрелком за 3 выстрела, построить многоугольник распределения, вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
|
|
|
Решение.
Случайная величина 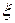 может принимать 4 значения:
может принимать 4 значения:
0 – если стрелок промахнулся 3 раза;
5 – если стрелок попал 1 раз при трех выстрелах;
10 – если стрелок попал 2 раза при трех выстрелах;
15 – если стрелок попал 3 раза.
Так как каждый выстрел можно рассматривать, как независимое испытание, в результате которого возможны только два исхода: попадание («успех») или промах («неудача»), то вероятности, соответствующие каждому значению случайной величины, можно найти по формуле Бернулли (5):
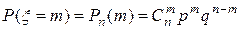 .
.
По условию задачи имеем: число испытаний 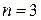 , вероятность успеха
, вероятность успеха 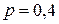 ,
, 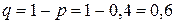 , значения
, значения 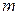 будут изменяться от 0 до 3. Т.о. имеем:
будут изменяться от 0 до 3. Т.о. имеем:
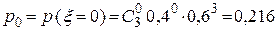 ,
,
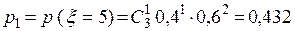 ,
,
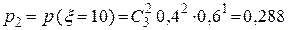 ,
,
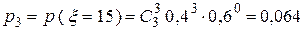 .о
.о
Следовательно, окончательно закон распределения случайной величины 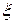 будет иметь вид:
будет иметь вид:
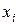
| 0 | 5 | 10 | 15 |
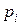
| 0,216 | 0,432 | 0,288 | 0,064 |
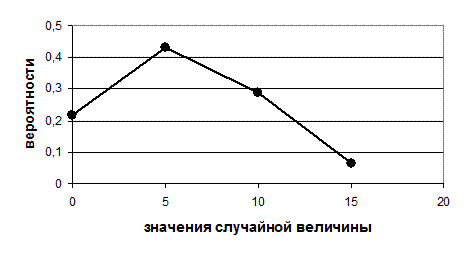
Построим многоугольник распределения. Для этого по оси абсцисс отложим возможные значения случайной величины, а по оси ординат – соответствующие им вероятности и соединяем точки (xi, pi) отрезками прямых. Полученная при этом ломаная линия и есть многоугольникраспределения вероятностей случайной величины 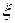 .
.
|
|
|
|
| Рис. 1. Многоугольник распределения вероятностей |
Рассчитаем числовые характеристики случайной величины 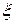 .
.
1. Математическое ожидание вычисляем по формуле (7)
 .
.
2. Дисперсия вычисляется по формуле (9):
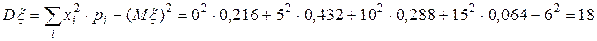 .
.
3. Среднее квадратическое отклонение
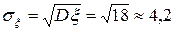 .
.
Ответ. Закон распределения случайной величины 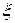 :
:

| 0 | 5 | 10 | 15 |
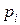
| 0,216 | 0,432 | 0,288 | 0,064 |
многоугольник распределения – на рисунке 1, 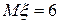 ,
,  ,
, 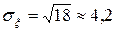 .
.
Задача 3. Случайная величина 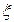 распределена по нормальному закону с математическим ожиданием
распределена по нормальному закону с математическим ожиданием 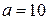 и дисперсией
и дисперсией 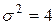 . Найти вероятность того, что в результате испытания
. Найти вероятность того, что в результате испытания 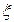 примет значение, заключенное в интервале
примет значение, заключенное в интервале 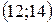 .
.
Решение.
Так как случайная величина 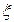 имеет нормальное распределение, то вероятность ее попадания в интервал можно найти по формуле (11). Учитывая, что по условию имеем:
имеет нормальное распределение, то вероятность ее попадания в интервал можно найти по формуле (11). Учитывая, что по условию имеем:  ,
, 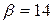 ,
, 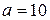 ,
,  , то получим:
, то получим:
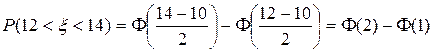 .
.
По таблице значений функции Лапласа 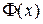 находим: F(2)=0,4772, F(1)=0,3413. Значит, получаем:
находим: F(2)=0,4772, F(1)=0,3413. Значит, получаем: 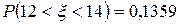 .
.
Ответ: 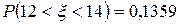
Задача 4. По выборке из генеральной совокупности нормально распределенного количественного признака X найти: 1) числовые характеристики выборки – выборочную среднюю, выборочную дисперсию, среднее квадратическое отклонение; 2) несмещенные оценки для генеральной средней и генеральной дисперсии; 3) доверительный интервал для оценки генеральной средней с надежностью 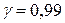 .
.
|
|
|

| 33,2 | 38,2 | 43,2 | 48,2 | 53,2 |
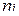
| 2 | 4 | 10 | 3 | 1 |
Решение.
1. Сначала вычислим числовые характеристики выборки.
Выборочную среднюю найдем по формуле (14).
Учитывая, что объем выборки 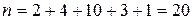 , получаем:
, получаем:
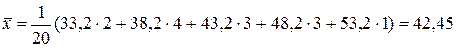 .
.
Выборочную дисперсию удобнее вычислять по формуле (16):
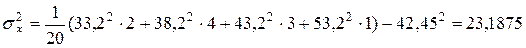 .
.
Выборочное СКО:
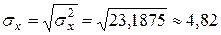 .
.
2. Несмещенной оценкой для генеральной средней 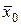 является выборочная средняя
является выборочная средняя 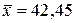 .
.
Несмещенной оценкой дисперсии  генеральной совокупности является исправленная выборочная дисперсия
генеральной совокупности является исправленная выборочная дисперсия 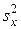 , которая вычисляется по формуле (17):
, которая вычисляется по формуле (17):
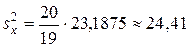 .
.
3. Так как генеральная дисперсия 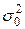 неизвестна, а известна лишь ее оценка – исправленная выборочная дисперсия
неизвестна, а известна лишь ее оценка – исправленная выборочная дисперсия  и данная выборка имеет небольшой объем (
и данная выборка имеет небольшой объем ( 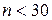 ), то доверительный интервал для генеральной средней можно найти, используя формулы (19) и (21).
), то доверительный интервал для генеральной средней можно найти, используя формулы (19) и (21).
Значение 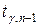 находим по таблице распределения Стьюдента, где
находим по таблице распределения Стьюдента, где  – доверительная вероятность,
– доверительная вероятность, 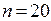 – объем выборки,
– объем выборки, 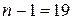 - число степеней свободы.
- число степеней свободы.
Учитывая, что 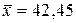 ,
, 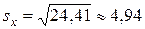 ,
, 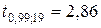 , находим сначала точность оценки по формуле (21):
, находим сначала точность оценки по формуле (21):
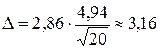 .
.
Теперь искомый доверительный интервал определяем по формуле (19):
|
|
|
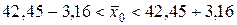
или 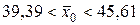 .
.
Ответы: 1. 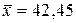 ,
, 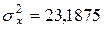 ,
, 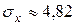 ; 2.
; 2. 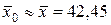 ,
, 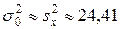 ; 3.
; 3. 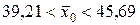 .
.
Задача 5. Массовую долю (%) оксида меди в минерале определили методом иодометрии и методом комплексометрии. По первому методу получили результаты: 38,20; 38,00; 37,66, а по второму: 37,70; 37,65; 37,55. Проверить, различаются ли средние результаты данных методов на уровне значимости  , если известно, что результаты измерений имеют нормальный закон распределения с неизвестными, но равными дисперсиями.
, если известно, что результаты измерений имеют нормальный закон распределения с неизвестными, но равными дисперсиями.
Решение.
Вычисляем для каждого метода числовые характеристики, учитывая, что объем каждой выборки равен  :
:
· выборочные средние значения по формуле (14):
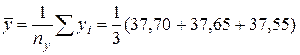 =37,63;
=37,63;
· исправленные выборочные дисперсии по формуле (18):
 ,
, 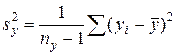
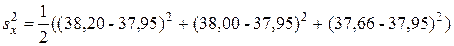 =0,07453;
=0,07453;
 =0,00583.
=0,00583.
Теперь проверим гипотезу о равенстве средних двух совокупностей.
1. Нулевая гипотеза: 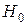 :
: 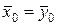 .
.
Альтернативная гипотеза:  :
: 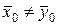
2. Уровень значимости 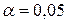 .
.
3. Проверку гипотезы будем проводить с помощью 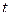 -критерия, так как выборки маленькие и по условию дисперсии генеральных совокупностей неизвестны, но равны. По таблице значений
-критерия, так как выборки маленькие и по условию дисперсии генеральных совокупностей неизвестны, но равны. По таблице значений 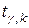 распределения Стьюдента при
распределения Стьюдента при  и числе степеней свободы
и числе степеней свободы 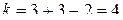 находим критическое значение:
находим критическое значение: 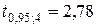 .
.
4. Рассчитаем эмпирическое значение 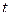 -критерия, используя формулу (22):
-критерия, используя формулу (22):
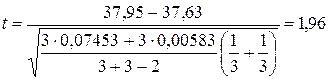 .
.
Сравним полученное значение 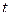 с табличным значением
с табличным значением 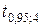 . Так как
. Так как  , то гипотеза
, то гипотеза 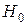 принимается.
принимается.
5. Гипотеза о равенстве средних значений двух методов проверена на уровне значимости 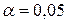 с помощью
с помощью 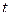 -критерия и принята. Следовательно, результаты обоих методов отражают истинное содержание
-критерия и принята. Следовательно, результаты обоих методов отражают истинное содержание 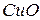 в минерале.
в минерале.
Ответ: гипотеза 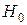 о равенстве средних проверена на уровне значимости
о равенстве средних проверена на уровне значимости 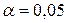 с помощью
с помощью 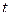 -критерия и принята.
-критерия и принята.
Задача 6. Имеются следующие данные об уровне механизации работ  (%) и производительности труда
(%) и производительности труда 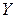 (т/чел.) для 14 однотипных предприятий:
(т/чел.) для 14 однотипных предприятий:
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

| 30 | 32 | 36 | 40 | 41 | 47 | 54 |

| 24 | 20 | 28 | 30 | 31 | 33 | 37 |
| № п/п | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

| 55 | 56 | 60 | 61 | 67 | 69 | 76 |
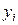
| 40 | 34 | 38 | 41 | 43 | 45 | 48 |
Требуется: 1) оценить тесноту и направление связи между признаками с помощью коэффициента корреляции и оценить значимость коэффициента корреляции на уровне значимости 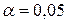 ; 2) найти уравнение линейной регрессии
; 2) найти уравнение линейной регрессии  на
на 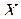 ; 3) в одной системе координат построить эмпирическую и теоретическую линии регрессии.
; 3) в одной системе координат построить эмпирическую и теоретическую линии регрессии.
Решение.
1. Для удобства проведем все необходимые предварительные расчеты в таблице.
Таблица 1
Расчетная таблица
| № п/п | 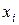
| 
| 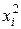
| 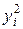
| 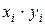
|
| 1 | 30 | 24 | 900 | 576 | 720 |
| 2 | 32 | 20 | 1024 | 400 | 640 |
| 3 | 36 | 28 | 1296 | 784 | 1008 |
| 4 | 40 | 30 | 1600 | 900 | 1200 |
| 5 | 41 | 31 | 1681 | 961 | 1271 |
| 6 | 47 | 33 | 2209 | 1089 | 1551 |
| 7 | 54 | 37 | 2916 | 1369 | 1998 |
| 8 | 55 | 40 | 3025 | 1600 | 2200 |
| 9 | 56 | 34 | 3136 | 1156 | 1904 |
| 10 | 60 | 38 | 3600 | 1444 | 2280 |
| 11 | 61 | 41 | 3721 | 1681 | 2501 |
| 12 | 67 | 43 | 4489 | 1849 | 2881 |
| 13 | 69 | 45 | 4761 | 2025 | 3105 |
| 14 | 76 | 48 | 5776 | 2304 | 3648 |
| Всего | 724 | 492 | 40134 | 18138 | 26907 |
Рассчитаем числовые характеристики выборки, используя итоговую строку расчетной таблицы и учитывая, что объем выборки 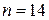 :
:
· выборочные средние:
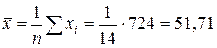 ;
;
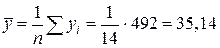 ;
;
· средние по квадратам:
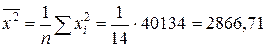 ;
;
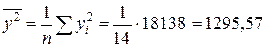 ;
;
· средняя по произведениям:
 ;
;
· выборочные средние квадратические отклонения:
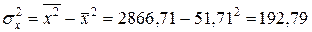 ;
;  ;
;
 ;
; 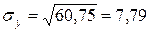 .
.
Вычислим выборочный коэффициент корреляции по формуле (26):
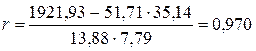 .
.
Т.к. 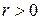 и
и 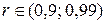 , то, следовательно, линейная связь между изучаемыми признаками является прямой и весьма тесной.
, то, следовательно, линейная связь между изучаемыми признаками является прямой и весьма тесной.
Оценим значимость выборочного коэффициента корреляции. Для этого рассчитаем эмпирическое значение 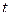 -критерия по формуле (26):
-критерия по формуле (26):
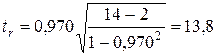 .
.
Для уровня значимости 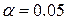 и числа степеней свободы
и числа степеней свободы 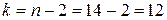 находим критическое значение
находим критическое значение 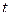 -критерия:
-критерия:  по таблице значений
по таблице значений 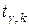 распределения Стьюдента. Поскольку
распределения Стьюдента. Поскольку 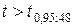 , то коэффициент корреляции между признаками
, то коэффициент корреляции между признаками 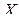 и
и  является значимым (или значимо отличается от нуля).
является значимым (или значимо отличается от нуля).
2. Найдем уравнение линейной регрессии  на
на 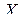 :
: 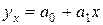 , вычислив параметры уравнения регрессии по формулам (23) и (24):
, вычислив параметры уравнения регрессии по формулам (23) и (24):
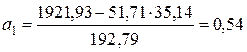 ;
;
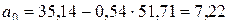 .
.
Следовательно, уравнение прямой регрессии имеет вид:
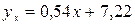 .
.
3) Построим в одной системе координат эмпирическую и теоретическую линии регрессии. Эмпирическая линия – это ломаная, соединяющая точки с координатами 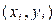 , а теоретическая – это график прямой регрессии, уравнение которой было получено в п. 2. Теоретическую линию регрессии можно построить по двум точкам, абсциссы которых выбираются произвольно, а ординаты находятся по построенному уравнению регрессии. Найдем координаты точек для построения теоретической линии регрессии:
, а теоретическая – это график прямой регрессии, уравнение которой было получено в п. 2. Теоретическую линию регрессии можно построить по двум точкам, абсциссы которых выбираются произвольно, а ординаты находятся по построенному уравнению регрессии. Найдем координаты точек для построения теоретической линии регрессии: 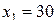 , тогда
, тогда 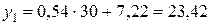 ;
; 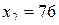 ,
, 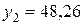 . Значит, теоретическую линию регрессии будем строить по двум точкам с координатами
. Значит, теоретическую линию регрессии будем строить по двум точкам с координатами 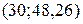 и
и 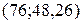 .
.
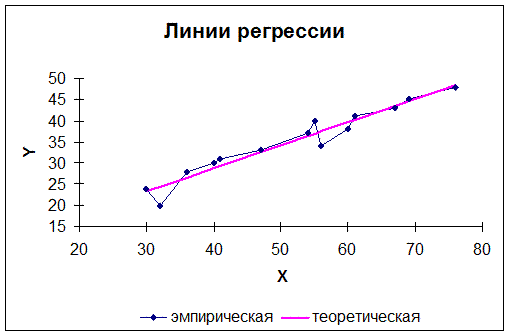
|
| Рис. 2. Эмпирическая и теоретическая линии регрессии |
Ответ: 1)  , линейная связь прямая, весьма тесная, коэффициент корреляции значим на уровне значимости
, линейная связь прямая, весьма тесная, коэффициент корреляции значим на уровне значимости 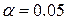 ; 2) выборочное уравнение прямой регрессии
; 2) выборочное уравнение прямой регрессии 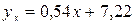 ; 3) линии регрессии представлены на рис. 2.
; 3) линии регрессии представлены на рис. 2.
Задача 7. Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно 3. Найти вероятность того, что за 2 минуты поступит: 1) четыре вызова; 2) менее четырех вызовов; 3) не менее четырех вызовов.
Решение.
Случайные события – заказы такси – представляют собой процесс Пуассона  .
.
По условию имеем: интенсивность потока – среднее число заказов в единицу времени –  , промежуток времени
, промежуток времени 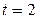 .
.
1) Искомая вероятность того, что за 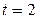 минуты поступит ровно
минуты поступит ровно 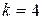 вызова можно вычислить по формуле (28). Имеем:
вызова можно вычислить по формуле (28). Имеем:
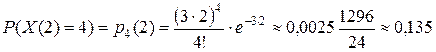 .
.
2) Событие "поступило менее четырех вызовов" произойдет, если за время 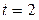 мин. наступит одно из следующих несовместных событий: «поступило три вызова» –
мин. наступит одно из следующих несовместных событий: «поступило три вызова» – 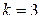 , «поступило два вызова» –
, «поступило два вызова» – 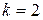 , «поступил один вызов» –
, «поступил один вызов» – 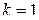 , «не поступило ни одного вызова» –
, «не поступило ни одного вызова» –  . Таким образом, искомую вероятность находим с помощью теоремы сложения вероятностей (1):
. Таким образом, искомую вероятность находим с помощью теоремы сложения вероятностей (1):
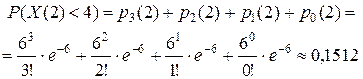
3) События "поступило не менее четырех вызовов" и "поступило менее четырех вызовов" противоположны, поэтому искомую вероятность того, что за две минуты поступит не менее 4 вызовов, можно найти по формуле (3):
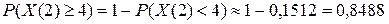 .
.
Ответы: 1) 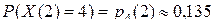 ; 2)
; 2)  ; 3)
; 3) 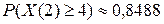
СПИСОК ЛИТЕРАТУРЫ
1. Кремер, Н. Ш. Теория вероятностей и математическая статистика : учеб. для вузов / Н. Ш. Кремер. – М. : ЮНИТИ-ДАНА, 2002. – 543 с.
2. Письменный, Д. Т. Конспект лекций по теории вероятностей и математической статистике / Д.Т. Письменный. – М. : Айрис-пресс, 2004. – 256 с. – (Высшее образование).
3. Гмурман, В. Е. Теория вероятностей и математическая статистика : учеб. пособие для вузов / В. Е. Гмурман. – М. : Высш. шк., 1997. – 479 с. : ил.
4. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике / В. Е. Гмурман. – М. : Высш. шк., 1998. – 400 с. : ил.
5. Данко, П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2 : учеб. пособие для вузов. / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. – М. : Оникс : Мир и образование, 2005. – 416 с.
[1] Понятия “элементарное событие” и “происходит” являются первоначальными неопределяемыми понятиями, подобно геометрическим понятиям “точка” и “лежит”. При общих рассуждениях полезно иметь в виду какой-либо простой конкретный эксперимент типа общепонятного бросания монеты, игральной кости, извлечения карты из колоды и т.п.
[2] Построение интервальных вариационных рядов целесообразно не только при непрерывной вариации признака, но и если дискретная вариация проявляется в широких пределах, т.е. число вариантов дискретного признака достаточно велико.
Дата добавления: 2019-02-22; просмотров: 246; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
