Приведение сил инерции для различных видов движения
В случае поступательного движения тела силы инерции, действующие на его точки, образуют систему параллельных сил, так как ускорения всех точек тела равны по величине и направлению, например, ускорению центра масс тела -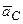 
. Система параллельных сил эквивалентна одной силе (равнодействующей), которая равна сумме всех сил системы и приложена в центре масс тела. В случае поступательного движения силы инерции приводятся к одной силе:
.
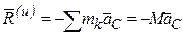В случае вращательного движения тела, обладающего плоскостью материальной симметрии, вокруг оси, перпендикулярной этой плоскости и проходящей через центр масс тела, силы инерции могут быть приведены к паре сил с моментом, равным главному моменту сил инерции относительно оси вращения:
.
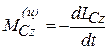Учитывая, что: 
, находим, что в этом случае силы инерции могут быть приведены к паре сил, с моментом, равным главному моменту сил инерции относительно оси вращения:
.
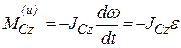В случае когда ось вращения Oz не проходит через центр масс тела, силы инерции приводятся к силе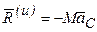 
, приложенной в точке О, и паре сил с моментом 
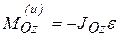, лежащей в плоскости симметрии тела.
При плоском движении тела, имеющего плоскость симметрии и движущегося параллельно этой плоскости, силы инерции приводятся к силе, приложенной в центре масс тела и равной главному вектору сил инерции 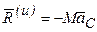, и паре сил с моментом, равным главному моменту сил инерции относительно оси, проходящей через центр масс:
|
|
|
.
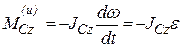Принцип возможных перемещений
Определение: возможным называется бесконечно малое перемещение системы, которое допускают наложенные на нее связи. На рис. 27 показано возможное перемещение системы.
Направление возможных перемещений совпадает с направлением скоростей точек и угловых скоростей звеньев механизма. Перемещение из положения ОАВ в положение ОА1В1 не является возможным, так как оно конечное.
Определение: связь называется идеальной, если работа ее реакции на любом возможном перемещении равна нулю (например, гладкая поверхность).
Для равновесия системы с идеальными двухсторонними связями необходимо и достаточно, чтобы сумма работ активных сил, действующих на нее, на любом возможном перемещении равнялась нулю:
. (53)
Общее уравнение динамики
Если к активным силам, действующим на систему с идеальными связями добавить силы инерции, то сумма работ этих сил на любом возможном перемещении будет равна нулю:
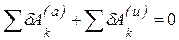. (54)
Общее уравнение динамики является суммой двух принципов: принципа Даламбера и принципа возможных перемещений. Действительно, если к неуравновешенной системе сил, действующей на механическую систему, добавить силы инерции, то согласно принципу Даламбера такая система сил будет уравновешенной и, следовательно, согласно принципу возможных перемещений
|
|
|
. (55)
Но, поскольку связи, наложенные на систему, являются идеальными, то сумма работ их реакций на любом возможном перемещении равна нулю: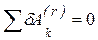 
. С учетом этого формула (55) примет вид (54).
Уравнение Лагранжа II рода
Уравнение Лагранжа II рода имеет вид:
, i = 1,…, n . (57)
Здесь обозначено: T – кинетическая энергия системы;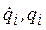 
– соответственно обобщенная скорость и обобщенная координата. Скорость и координата называются обобщенными, поскольку могут быть как линейными, так и угловыми. 
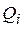- обобщенная сила ( может быть как силой, так и моментом); n – число степеней свободы системы. число степеней свободы системы с геометрическими связями (геометрическими называют связи, которые налагают ограничения на положение точек системы) равно числу независимых координат, с помощью которых можно однозначно определить положение системы. В общем случае точка системы может иметь бесконечное число возможных перемещений, но всегда найдется несколько возможных перемещений, через которые можно линейно выразить все остальные. Именно они и называются независимыми. Например, любое перемещение точки на плоскости можно выразить через два перемещения, соответствующие координатам x и y. Таким образом, точка на плоскости имеет две степени свободы. Вращающееся тело имеет одну степень свободы, так как его положение можно однозначно определить, задав всего одно перемещение – угол поворота. Обобщенную силу находят по формуле:
|
|
|
,
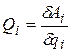где 
- работа сил, действующих на систему на возможном перемещении, при котором изменяется только обобщенная координата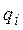 
.
Например, для точки на рис. 28 обобщенные силы, соответствующие координатам x и y можно найти по формулам:
,
.
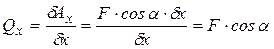Дата добавления: 2019-02-12; просмотров: 173; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!