Момент инерции однородного стержня

Найдем момент инерции однородного стержня длиной 2l относительно оси z, проходящей через его центр масс (рис. 21).

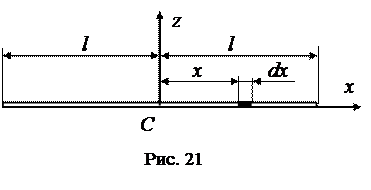
Пусть γ – линейная плотность стержня (масса единицы его длины, кг/м). Выделим на расстоянии х от оси Сz элементарный отрезок длиной dx . Момент инерции этого элементарного отрезка относительно оси

Сz: .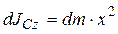

Но 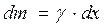, тогда 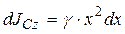. Проинтегрировав это выражение, получаем

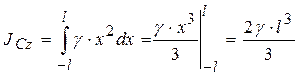Но γ ∙2 l = m – масса стержня.

Окончательно момент инерции однородного стержня длиной 2l относительно центральной оси

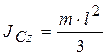Момент инерции однородного кольца

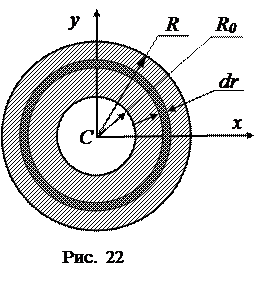
Найдем момент инерции однородного кольца относительно оси Сz ,, проходящей через его центр масс (рис. 22).

Пусть γ – поверхностная плотность кольца (масса единицы его площади), кг/м². Выделим на расстоянии r от оси Сz элементарное кольцо толщиной dr . Момент инерции этого элементарного кольца относительно оси Сz: .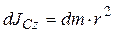

Но 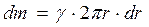, тогда .

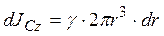Проинтегрировав это выражение, получаем

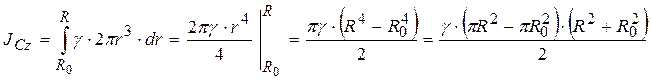
Но 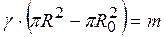– масса кольца.

Окончательно момент инерции однородного кольца относительно центральной оси

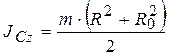. (35)

Для однородного диска радиуса R (R₀=0) из (35) имеем: .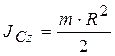

В случае, когда масса распределена по ободу, R₀= R и .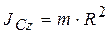

Теорема Гюйгенса

Для системы точек, показанной на рис. 23, момент инерции относительно оси О z можно найти по формуле (34).

Выберем ось Ox так, что бы она проходила через центр масс системы (т. С). Пусть расстояние между осями z и z ОС = d. Свяжем с т. С новую систему координат С x ₁ y ₁ z ₁ . Очевидно, что координаты точек в системах Oxyz и С x ₁ y ₁ z ₁ связаны между собой соотношениями

x_k = x_1k+d, y_k = y_1k, z_k = z_1k,.

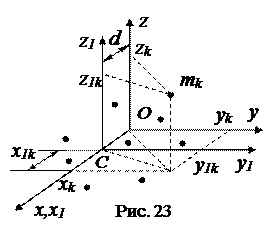
Тогда .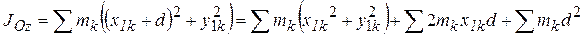

Но 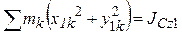; 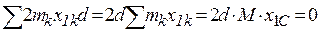(см. (33′)), 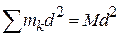. С учетом этого

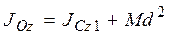. (36)

Формула (36) связывает моменты инерции относительно параллельных осей и выражает теорему Гюйгенса: момент инерции системы точек относительно произвольной оси, параллельной центральной, складывается из центрального момента инерции и произведения массы системы на квадрат расстояния между осями.

Теорема о движении центра масс

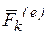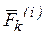Пусть имеется система точек, на каждую из которых действуют внешние и внутренние силы. Обозначим равнодействующие этих сил, приложенных к точке с номером k, соответственно и . Запишем основное уравнение динамики для точки с номером k: 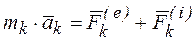. Записывая подобные уравнения для каждой точки системы, и суммируя их, получим

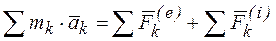. (37)

По свойствам внутренних сил (32) 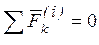. Кроме того, взяв вторую производную от равенства (33) , получим

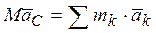С учетом этого формула (37) примет вид:

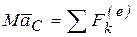. (38)

Формула (38) выражает теорему о движении центра масс: центр масс системы двигается как материальная точка, в которой сосредоточена масса всей системы и к которой приложены все внешние силы, действующие на ее точки.

Теорема об изменении количества движения системы

Определение: количеством движения системы точек называется вектор 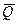, равный геометрической сумме количеств движения всех точек системы:

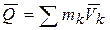Запишем теорему об изменении количества движения для точки с номером k:

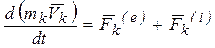. Здесь, как и ранее, 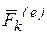и 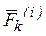– соответственно равнодействующие внешних и внутренних сил, приложенных к точке с номером k. Записывая подобные уравнения для каждой точки системы и, суммируя их, получим

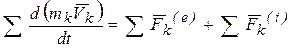учитывая, что 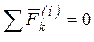, получим, поменяв местами, знаки суммирования и дифференцирования в левой части равенства:

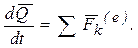(39)

Формула (39) выражает теорему об изменении количества движения системы точек в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме внешних сил, действующих на ее точки.

Умножив равенство (39) на dt и проинтегрировав, получим теорему об изменении количества движения системы точек в интегральной форме:

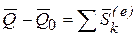, (40)

где 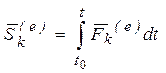– импульс силы .

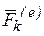Дата добавления: 2019-02-12; просмотров: 270; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!