Кинетический момент твердого тела, вращающегося вокруг
Неподвижной оси
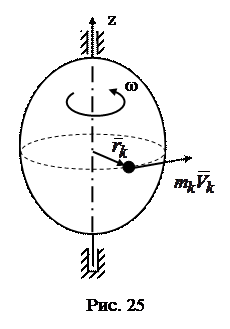
Твердое тело, вращающееся вокруг неподвижной оси z (рис. 25), можно рассматривать как систему точек. Момент количества движения этой системы относительно оси z называют кинетическим моментом твердого тела относительно оси вращения:
.
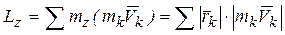Учитывая, что при вращательном движении:
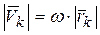, а 
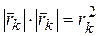, получим
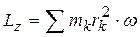. По формуле (34) получим
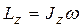(45)
– кинетический момент твердого тела вращающегося вокруг неподвижной оси равен произведению момента инерции тела относительно оси вращения на его угловую скорость.
Теорема об изменении кинетической энергии системы
Определение: кинетической энергией системы точек называется скалярная
величина равная сумме кинетических энергий всех точек системы:
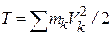
Запишем теорему об изменении кинетической энергии для точки с номером k:
,
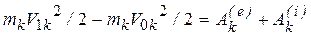где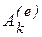 
и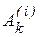 
- соответственно работа внешних и внутренних сил действующих на точку с номером k. Записывая подобные уравнения для каждой точки системы, и суммируя их, получим
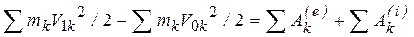. (46)
По определению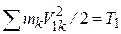 
, а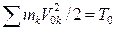 
. Тогда (45) примет вид:
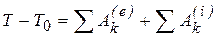. (47)
Формула (47) выражает теорему об изменении кинетической энергии системы: изменение кинетической энергии системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на точки системы на том же перемещении.
|
|
|
Аналогично можно получить теорему об изменении кинетической энергии системы в дифференциальной форме:
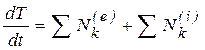
– производная по времени от кинетической энергии системы равна сумме мощностей внешних и внутренних сил, действующих на ее точки.
Кинетическая энергия твердого тела в различных случаях движения.
Поступательное движение.
В этом случае скорости всех точек тела одинаковы. Тогда: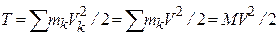 
– кинетическая энергия тела при поступательном движении равна половине произведения массы тела на его скорость.
Вращательное движение
В этом случае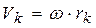 
. Тогда
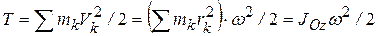
– кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.
Плоское движение
Плоское движение в данный момент можно рассматривать, как вращательное вокруг мгновенного центра скоростей (т. Р, рис. 26).
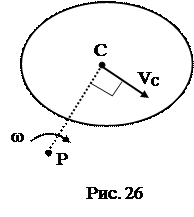
Тогда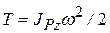 
. Но по теореме Гюйгенса (36)
.
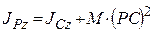Тогда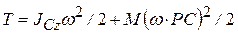 
. Но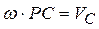 
.
Окончательно получаем
.
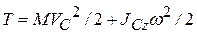Из этой формулы видно, что кинетическая энергия при плоском движении состоит из двух слагаемых, первое из которых соответствует поступательному движению тела вместе с центром масс, а второе – вращательному движению вокруг оси, проходящей через центр масс.
|
|
|
Дифференциальные уравнения поступательного
И вращательного движения твердого тела
При поступательном движении все точки тела двигаются одинаково, поэтому для описания поступательного движения твердого тела достаточно описать движение хотя бы одной его точки. Если в качестве этой точки выбрать центр масс тела (т. С), то для этого можно использовать теорему о движении центра масс (38) или в проекции на оси координат:
; 
; 
.
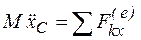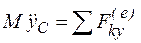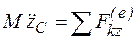Для описания вращательного движения воспользуемся теоремой об изменении момента количества движения системы (44) в проекции на ось z (ось вращения):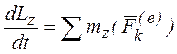 
. Кинетический момент твердого тела относительно оси вращения найдем по формуле (45). В результате получим: 
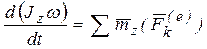. Поскольку момент инерции тела – величина постоянная: Jz = const, то, вынеся его за знак производной, получим 
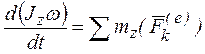или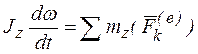 
– это и есть дифференциальное уравнение вращательного движения твердого тела. Поскольку 
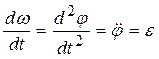- угловое ускорение, то это уравнение можно записать в виде: 
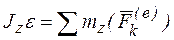или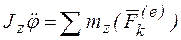 
. Можно заметить, что это уравнение по своей структуре аналогично основному уравнению динамики (1). При его решении могут возникнуть две задачи динамики: прямая и обратная.
|
|
|
Дата добавления: 2019-02-12; просмотров: 472; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!