Изменение количества движения системы точек за некоторый промежуток времени равно сумме импульсов внешних сил, действующих на её точки за тот же промежуток времени.
Теоремы (39) и (40) – векторные, их можно записать в проекции на оси координат. Закон сохранения количества движения системы вытекает из формул (39) и (40): если в течение некоторого промежутка времени, сумма внешних сил, действующих на точки системы, равна нулю, то ее количество движения все это время остается неизменным.
Связь между количеством движения системы, массой системы
И скоростью ее центра масс
взяв производную по времени от равенства (33) получим, учитывая, что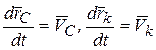 
: 
.
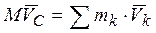Но по определению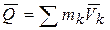 
, тогда
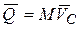. (41)
Количество движения системы равно произведению массы системы на скорость ее центра масс.
Применение теоремы об изменении количества движения системы
К сплошным средам
Рассмотрим стационарный поток жидкости, т.е. такой, у которого в каждой точке скорость, давление и плотность остаются неизменными с течением времени. В случае ламинарного течения (жидкость перемещается слоями, без перемешивания) траектории частиц жидкости являются линиями тока.
Выделим в потоке жидкости (рис. 24) объем, ограниченный линиями тока и двумя сечениями 1 и 2.
Пусть за малое время dt этот объем переместился из положения 1-2 в положение 3-4. Тогда изменение его количества движения: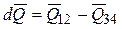 
. Но 
.
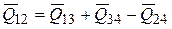С учетом этого
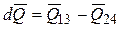. (42)
|
|
|
Обозначим секундный массовый расход жидкости МС (масса жидкости, протекающая через сечение трубки тока за одну секунду), кг/м. Учитывая, что при ламинарном потоке ни одна частица жидкости не выходит за границы трубки тока, то по закону сохранения вещества расход жидкости в любом сечении трубки тока одинаков: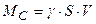 
, где
γ – объемная плотность жидкости, кг/м3; S и V – соответственно площадь произвольного сечения трубки тока и скорость жидкости в этом сечении.
тогда: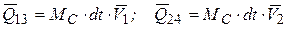 
и формула (42) принимает вид: 
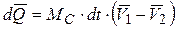. Подставив это выражение в теорему об изменении количества движения системы в дифференциальной форме (39), получим
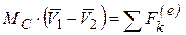. (43)
Произведение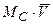 
- называют секундным количеством движения. Тогда разность секундных количеств движения жидкости в двух сечениях трубки тока равна сумме объемных и поверхностных сил, действующих на ее частицы, заключенные между этими сечениями.
Теорема об изменении момента количества движения системы
Моментом количества движения системы точек относительно центра О называется вектор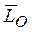 
, равный геометрической сумме векторов моментов количества движения всех точек системы относительно того же центра:
|
|
|
.
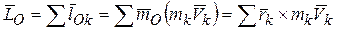Теорема: Производная по времени от момента количества движения системы точек относительно центра О равна сумме моментов внешних сил, действующих на точки системы относительно того же центра.
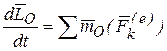(44)
Доказательство. Запишем теорему об изменении момента количества движения для точки с номером k: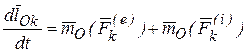 
.
Записывая подобные уравнения для каждой точки системы, и суммируя их, получим: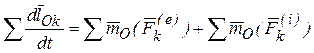 
.
Учитывая, что по свойствам внутренних сил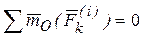 
, получим, поменяв местами знаки суммирования и дифференцирования в левой части уравнения: 
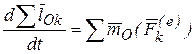, или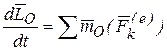 
. Что и требовалось доказать.
Теорема об изменении момента количества движения точки векторная, поэтому её можно записать в проекциях на оси координат:
; 
; 
.
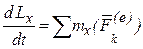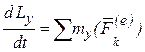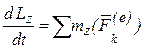Закон сохранения: Если в течение некоторого времени сумма моментов внешних сил, действующих на точки системы, относительно центра О равна нулю, то момент количества движения системы относительно этого центра все это время остается неизменным.
Дата добавления: 2019-02-12; просмотров: 178; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!