Методика вивчення степеневої функцii.
Степенева функція. З окремими випадками степеневої функції учні ознайомлювалися в 7 і 8 класах (у = х , у = х , у = у/х). Однак на тому етапі навчання термін «степенева функція» та відповідне означення не вводились, оскільки поняття степеня не розширювалось до степеня з дійсним показником.
Запровадивши степінь з дійсним показником хр, виявляємо, що за заданого дійсного значення р кожному додатному х можна поставити у відповідність числове значення степеня хр. Отже, за сталого дійсного показника р і змінного додатного х матимемо функцію у = хр, яку називають степеневою.
Властивості степеневої функції залежать від заданого значення р.
Доцільно розглянути різні можливі множини значень р.
І. Нехай р - натуральне число.
Наведемо властивості функції.
1. Областю визначення функції є множина R всіх дійсних чисел. Область значень залежить від парності чи непарності р. Якщо р парне, то область значень у = хрє множиною невід'ємних чисел, якщо непарне, то - множиною R всіх дійсних чисел.
2. Функція парна за парного р і непарна за непарного р.
3. За х = 0 у = 0, за х = 1 у = 1, тобто всі графіки степеневих функцій проходять через початок координат і точку (1; 1).
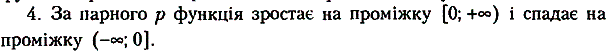
За непарного р функція зростає на всій області визначення.
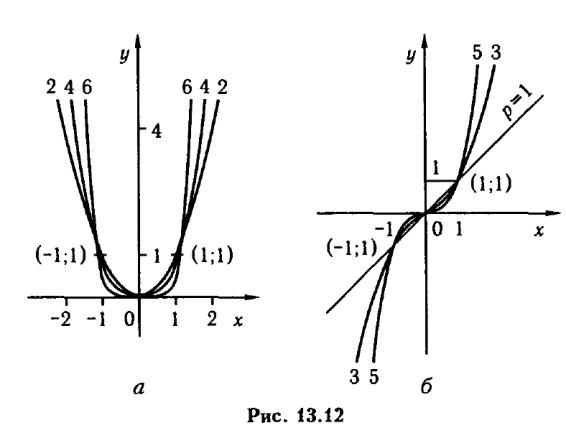
5. За парного р графіки степеневих функцій подібні до графіка функції у = х2 (рис. 13.12, а), а за непарного - до графіка функції у = х3 (рис. 13.12, б).
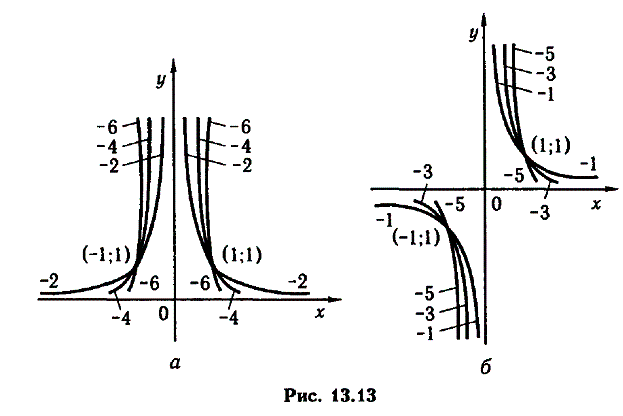
II. Нехай р - ціле від'ємне число.
|
|
|
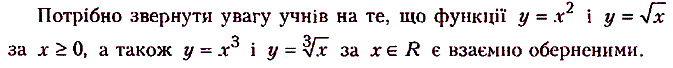
Методика введення поняття пох i дної.
У вузівських курсах математичного аналізу для підведення студентів до означення похідної здебільшого розв'язують обидві задачі Лейбніца і Ньютона. У шкільному курсі через обмеженість часу найчастіше докладно розглядають одну з цих задач. Перевагу слід віддати задачі про миттєву швидкість, оскільки з нею учні вже ознайомились в курсі фізики, а на цьому етапі навчання доцільно оформити її розв'язання в термінах і символах математичного аналізу (приріст аргументу, приріст функції, границя функції). При цьому варто в процесі розв'язування чітко виділити чотири кроки, які розкривають зміст похідної і які доцільно виконувати надалі при виведенні формул і доведенні основних теорем про похідні. Розглядаючи задачу про миттєву швидкість, треба звернути увагу учнів на те, що середня швидкість нерівномірного прямолінійного руху певною мірою характеризує його, проте вона часто не задовольняє потреб практики. Отже, виникає потреба вміти визначати швидкість у певний момент часу t0.
Щоб учні неформально сприйняли означення миттєвої швидкості, варто на прикладі конкретної задачі з числовими даними показати, що значення середньої швидкості прямує до певної границі, яку природно вважати числовим значенням швидкості в даний момент часу t0, тобто значенням миттєвої швидкості.
|
|
|
Означення. Похідною функції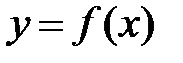 
в точці х0 називається границя відношення приросту 
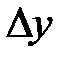функції до приросту 
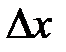аргументу за умови, що приріст 
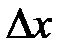аргументу прямує до нуля, а границя існує, тобто
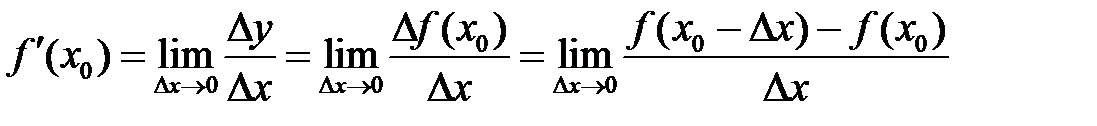
Зауважимо, що перш ніж вводити поняття похідної, варто привчити учнів до трьох різних символів, що стосуються приросту функції і відношень її до приросту аргументу. Після введення означення доцільно знайти за його допомогою похідні деяких функцій. Однак перед цим важливо наголосити, що коли похідну шукають у певній точці х0, то вона як границя є певним числом. Коли ж функція 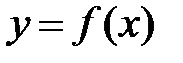має похідну в кожній точці х інтервалу (а;b),то кожному значенню х відповідає певне значення похідної. Отже, в такому разі похідна функції 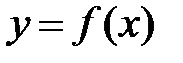на інтервалі (а;b) єтеж функцією, яку позначають символом 
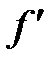або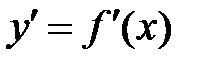 
Коли функцію задано формулою, наприклад, 
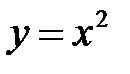, то похідну позначають символом 
.
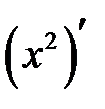Для більш глибокого усвідомлення учнями означення похідної доцільно зразу ж з'ясувати її механічний і геометричний зміст. Механічний зміст похідної випливає з розглянутої задачі Про миттєву швидкість. Учні самі здатні зробити висновок, що похідна дорівнює миттєвій швидкості нерівномірного руху. Цим самим з'ясовується механічний зміст похідної.
|
|
|
Геометричний зміст похідної випливає із задачі про дотичну до кривої у певній точці: похідна в точці х0 дорівнює тангенсу кута нахилу дотичної до кривої з додатним напрямком осі х у точці з абсцисою х0.
З метою закріплення означення і алгоритму відшукання похідної за означенням (послідовним виконанням чотирьох кроків) корисно запропонувати учням у класі і як домашнє завдання обчислити похідні функцій.
Основні правила диференціювання функції:
1) якщо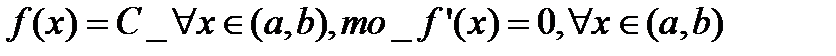 
, тобто похідна від сталої функції дорівнює нулю ( 
);
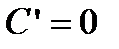2) похідна незалежної змінної х дорівнює 1: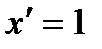 
;
3) якщо функція f(x) диференційована в т. х, то і функція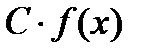 
, де С-стале, також диференційовна в т. х, причому 
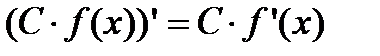, тобто сталий множник можна виносити за знак похідної;
4) якщо функції f(x) і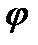 
(x) диференційовні в точці х, то і їх сума, різниця, добуток і частка також будуть диференційовні в точці х, причому
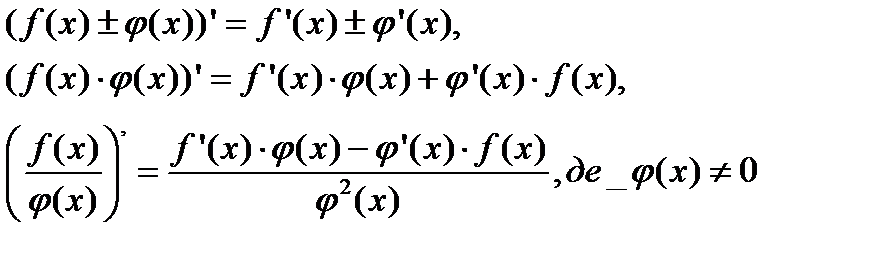
Основні теореми про похідні.
До таких слід віднести теореми: 1) про неперервність диференційованої в точці функції2) про похідну суми функцій; 3) про похідну добутку функцій; 4) про похідну частки двох функцій; 5) про похідну степеневої функції; 6) про похідну складної функції.
|
|
|
Дата добавления: 2019-02-12; просмотров: 387; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!