Зв’язок між географічною і першою екваторіальною системами координат.
Для встановлення зв’язку між географічною широтою  точки спостереження і схилянням
точки спостереження і схилянням  розглянемо рисунок 2.7. На ньому Земля представлена однорідною кулею, так що всі прямовисні лінії проходять через її центр
розглянемо рисунок 2.7. На ньому Земля представлена однорідною кулею, так що всі прямовисні лінії проходять через її центр  . Нехай в точці спостереження
. Нехай в точці спостереження  встановлено напрям прямовисної лінії
встановлено напрям прямовисної лінії 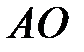 і продовжено його до перетину з топоцентричною небесною сферою в точці
і продовжено його до перетину з топоцентричною небесною сферою в точці  , яка буде точкою зеніту. Для точки спостереження
, яка буде точкою зеніту. Для точки спостереження  , гострий кут, утворений прямовисною лінією
, гострий кут, утворений прямовисною лінією  з площиною земного екватора
з площиною земного екватора  буде географічною широтою точки
буде географічною широтою точки  .
.
 Рисунок 2.7 – Зв’язок між
Рисунок 2.7 – Зв’язок між  і і 
| Оскільки вісь обертання Землі  паралельна до осі світу паралельна до осі світу  , то площина земного екватора , то площина земного екватора 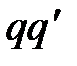 буде паралельною до площини небесного екватора буде паралельною до площини небесного екватора  і, таким чином, і, таким чином,  як кути між двома прямими, що перетинаються третьою. Але мірою як кути між двома прямими, що перетинаються третьою. Але мірою 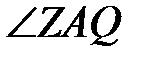 є сферична дуга є сферична дуга  , що дорівнює схиленню точки зеніту , що дорівнює схиленню точки зеніту  . .
|
Тому маємо
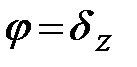 (2.3)
(2.3)
Формулюється ця теорема так.
Географічна широта точки спостереження дорівнює схиленню точки зеніту цієї точки.
Таким чином, якщо за допомогою тих чи інших методів для довільної точки місцевості встановити положення точки зеніту на небесній сфері і визначити схилення точки зеніту, то, тим самим, визначається географічна широта цієї точки місцевості. На основі рисунка 2.7 можна довести, що буде справедлива і така теорема про географічну широту.
Географічна широта точки спостереження  дорівнює висоті полюса світу над горизонтом
дорівнює висоті полюса світу над горизонтом  , тобто
, тобто
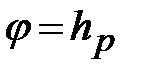 . (2.4)
. (2.4)
Ця теорема доводиться на основі положення геометрії про взаємно перпендикулярні прямі.
12.Класифікація зірок за добовим рухом .
Видимий добовий рух зір по небесній сфері є відображенням обертання Землі навколо своєї осі. Тому цей рух відбувається по колах, центри яких паралельні площині екватора. Вони дістали назву добових паралелей. Перетин добових паралелей з меридіаном точки спостереження утворює на небесній сфері точки кульмінації світил.
Для розгляду питань класифікації зір за їх видимим добовим рухом, побудуємо зображення топоцентричної сфери у вигляді ортогональної проекції її (збоку точки заходу) на площину небесного меридіана точки спостереження (рис. 3.1)
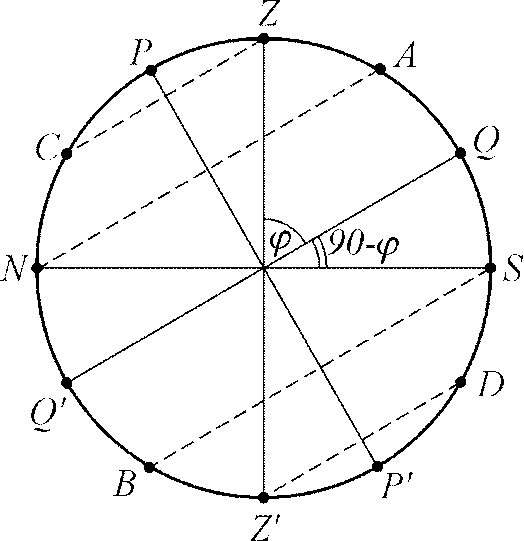
| Небесний екватор 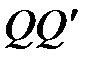 і небесний горизонт і небесний горизонт  на цьому рисунку відобразяться прямими лініями, кут між якими у відповідності з (2.3) дорівнює на цьому рисунку відобразяться прямими лініями, кут між якими у відповідності з (2.3) дорівнює  . Добові паралелі будуть прямими паралельними до екватора, а зображення першого вертикала співпадає з зображенням прямовисної лінії . Добові паралелі будуть прямими паралельними до екватора, а зображення першого вертикала співпадає з зображенням прямовисної лінії  .
Покладемо в основу класифікації зір умову перетину площини небесного горизонту добового паралеллю зірки. Якщо через точки .
Покладемо в основу класифікації зір умову перетину площини небесного горизонту добового паралеллю зірки. Якщо через точки
|
півдня  і півночі
і півночі  небесної сфери провести площини
небесної сфери провести площини  і
і 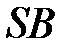 , паралельні до площини екватора
, паралельні до площини екватора 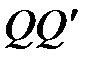 , то на небесній сфері виділяються три зони щодо видимого добового руху зір:
, то на небесній сфері виділяються три зони щодо видимого добового руху зір:
– зона, в якій знаходяться добові паралелі зір, що ніколи не заходять;
– зона, в якій знаходяться добові паралелі зір, що ніколи не сходять,
– зона, в якій знаходяться добові паралелі зір, що сходять і заходять.
На основі теореми сферичної астрономії про зв’язок географічної широти точки спостереження зі схиленням світил встановимо математичні критерії віднесення світил до тої чи іншої класифікаційної групи. Для того, щоб зірка була віднесена до групи тих, що в своєму добовому русі по небесній сфері ніколи не заходять, необхідне виконання умови
 (3.1)
(3.1)
Виконання умови (3.1) означає, що в такої зірки добова паралель буде розміщена вище граничної добової паралелі  (рис. 3.1) оскільки схилення таких зірок буде більшим від кута
(рис. 3.1) оскільки схилення таких зірок буде більшим від кута  .
.
За аналогією встановимо, що добові паралелі зір, які ніколи не сходять повинні розміщуватись нижче граничної добової паралелі  (рис. 17), що приводить до умови
(рис. 17), що приводить до умови
 , (3.2)
, (3.2)
оскільки для таких зір схилення повинно бути меншим від величини кута  .
.
Очевидно, що для зір, які входять в класифікаційну групу тих, що сходять і заходять повинна задовольнятись умова
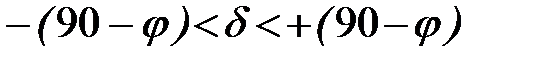 , (3.3)
, (3.3)
оскільки їх добові паралелі повинні знаходитись між граничними добовими паралелями  і
і 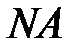 .
.
Іншою класифікаційною ознакою може стати умова перетину чи неперетину добовою паралеллю зірки площини першого вертикала. За цією ознакою зірки відносять до двох класифікаційних груп:
– зірки, що в своєму видимому добовому русі перетинають перший вертикал;
– зірки, що в своєму видимому добовому русі не перетинають перший вертикал.
Світила будуть відноситись до першої класифікаційної групи у випадку, коли їх схилення за абсолютною величиною не буде перевищувати величину дуги 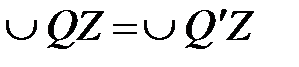 , тобто
, тобто
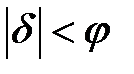 . (3.5)
. (3.5)
Світило не буде перетинати площину першого вертикала (світило буде мати елонгацію) у випадку виконання умови
 .
.
Дата добавления: 2019-02-12; просмотров: 155; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
