Определение фронтальной насыщенности.
Фронтальную насыщенность можно определять графически, используя графики функции Леверетта, либо аналитически, если известны функции относительных фазовых проницаемостей пористой среды для воды и нефти соответственно. Воспользуемся аналитическим методом, задав относительные фазовые проницаемости для воды 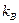 и нефти
и нефти  в наиболее простом виде:
в наиболее простом виде:
|
|  , (54) , (54)
|
|
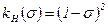 , (55) , (55)
|
|
где  – коэффициент водонасыщенности.
– коэффициент водонасыщенности.
Этим фазовым проницаемостям (54) и (55) отвечает следующая функция Леверетта  :
:
 , (56) , (56)
|
|
где  – относительный коэффициент вязкости.
– относительный коэффициент вязкости.
Производная функции Леверетта, исходя из выражения (56), будет определяться по формуле:
 . (57) . (57)
|
|
Формула для определения фронтальной насыщенности 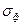 имеет вид:
имеет вид:
 , (58) , (58)
|
|
где 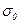 – коэффициент начальной водонасыщенности.
– коэффициент начальной водонасыщенности.
Численное решение уравнения (58) с учётом (56), (57) и того, что начальная водонасыщенность по условию составляет  , позволяет получить значение фронтальной насыщенности, которая составила
, позволяет получить значение фронтальной насыщенности, которая составила  (рисунок 11).
(рисунок 11).

|
Рисунок 12 – Графики функции Леверетта 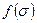 и вспомогательной функции и вспомогательной функции  , полученной из уравнения касательной к , полученной из уравнения касательной к 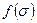
|
Следует отметить, что с ростом коэффициента относительной вязкости  происходит рост фронтальной насыщенности, а, следовательно, и эффективности вытеснения, так как доля воды в суммарном потоке уменьшается, поэтому на практике часто применяют пены и загустители, повышающие вязкость воды [10, с.63-64].
происходит рост фронтальной насыщенности, а, следовательно, и эффективности вытеснения, так как доля воды в суммарном потоке уменьшается, поэтому на практике часто применяют пены и загустители, повышающие вязкость воды [10, с.63-64].
|
|
|
Неустановившаяся фильтрация упругой жидкости в упругой пористой среде
Подсчёт упругого запаса жидкости в пласте
Под упругим запасом жидкости в пласте понимается количество жидкости, которое можно извлечь из пласта при снижении давления в нем за счёт объёмной упругости пласта и насыщающих его жидкостей. Величина упругого запаса жидкости  при снижении давления во всех точках пласта на величину
при снижении давления во всех точках пласта на величину  складывается из приращения объёма жидкости ввиду её расширения
складывается из приращения объёма жидкости ввиду её расширения  и сокращения объёма порового пространства
и сокращения объёма порового пространства  за счёт расширения материала пласта:
за счёт расширения материала пласта:
 . (59) . (59)
|
|
Все эти факторы способствует вытеснению жидкости из пласта в скважину.
Приращение объёма жидкости 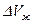 складывается из приращения объёмов нефти и воды соответственно, то есть
складывается из приращения объёмов нефти и воды соответственно, то есть
 , (60) , (60)
|
|
которые, в свою очередь, определяются по формулам:
|
|  , (61) , (61)
|
|
 , (62) , (62)
|
|
где  ,
,  – коэффициенты объёмной упругости нефти и воды соответственно, характеризующие их податливость к изменению объёма,
– коэффициенты объёмной упругости нефти и воды соответственно, характеризующие их податливость к изменению объёма,  ;
;
|
|
|
 ,
, 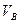 – объёмы нефти и воды соответственно, насыщающие некоторый элемент пласта
– объёмы нефти и воды соответственно, насыщающие некоторый элемент пласта  при начальном давлении,
при начальном давлении,  .
.
Учитывая, что начальный объем жидкости 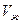 , насыщающей пласт объёмом
, насыщающей пласт объёмом 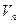 , равен начальному объёму пор пласта
, равен начальному объёму пор пласта  , имеем:
, имеем:
 , (63) , (63)
|
|
где  – коэффициент пористости [5, с.64-65].
– коэффициент пористости [5, с.64-65].
Для дальнейших рассуждений введём понятие коэффициента водонасыщенности  , который определяется как отношение общего объёма воды в поровом пространстве к объёму пор пласта [11, с.18]:
, который определяется как отношение общего объёма воды в поровом пространстве к объёму пор пласта [11, с.18]:
 . (64) . (64)
|
|
На основании формул (63) и (64) выразим объёмы нефти и воды через объём пласта:
|
|  , (65) , (65)
|
|
 . (66) . (66)
|
|
Окончательно, формула для подсчёта  может быть записана в следующем виде:
может быть записана в следующем виде:
 . (67) . (67)
|
|
Сокращение объёма порового пространства определяется по формуле
 , (68) , (68)
|
|
где  – коэффициент сжимаемости пористой среды [5, с.64].
– коэффициент сжимаемости пористой среды [5, с.64].
Из формул (59), (67) и (68) получим конечную формулу для расчёта упругого запаса жидкости в пласте:
|
|
|
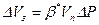 , (69) , (69)
|
|
где  – коэффициент упругоёмкости пласта:
– коэффициент упругоёмкости пласта:
 . (70) . (70)
|
|
По формуле (70) рассчитаем коэффициент упругоёмкости пласта:
 .
.
С учётом того, что объём пласта
 , (71) , (71)
|
|
упругий запас жидкости определим по формуле (69) следующим образом:
 .
.
Из расчёта видно, что наряду с малостью коэффициентов объемной упругой деформации жидкости и пласта, упругий запас жидкости в пласте оказался весьма существенным. Этот факт объясняется большими объёмами пласта.
Объём нефти, который можно отобрать из пласта за счёт упругого расширения жидкости и породы, также рассчитаем по формуле (69), но с поправкой на коэффициент водонасыщенности:
 .
.
Полный запас нефти определим по формуле (65) с учётом (71):
 .
.
Таким образом, за счёт энергии упругой деформации жидкостей и материала пласта из него можно извлечь меньше одного процента нефти.
Дата добавления: 2019-01-14; просмотров: 532; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
