Приток жидкости к скважине, эксцентрично расположенной в круговом пласте
Для определения дебита эксцентрично расположенной скважины в круговом пласте вводится функция  , называемая потенциалом скорости фильтрации. Потенциалом скорости фильтрации называется функция, производная которой с обратным знаком вдоль линии тока равна скорости фильтрации:
, называемая потенциалом скорости фильтрации. Потенциалом скорости фильтрации называется функция, производная которой с обратным знаком вдоль линии тока равна скорости фильтрации:
|
|  ; ;
| (7 |
 . .
| (8 |
Для расчёта введём также понятия точечного источника и стока.
Под точечным стоком понимается точка на плоскости, поглощающая жидкость, которую можно рассматривать как модель гидродинамически совершенной эксплуатационной скважины бесконечно малого радиуса в пласте единичной мощности.
Под точечным источником понимается точка, выделяющая жидкость, которую можно рассматривать как модель нагнетательной скважины.
Дебиты стоков принято считать положительными, дебиты источников – отрицательными.
Итак, найдём потенциал точечного стока на плоскости, вокруг которого будет наблюдаться плоскорадиальное движение:
 ,
,
 ,
,
где  – площадь фильтрации.
– площадь фильтрации.
После интегрирования получим выражение потенциала для точечного стока на плоскости:
 , ,
| (9 |
где  – расстояние от точки, в которой определяется потенциал, до точечного стока;
– расстояние от точки, в которой определяется потенциал, до точечного стока;
 – постоянная интегрирования [5, с.47-48].
– постоянная интегрирования [5, с.47-48].
Итак, если скважина находится в пласте с круговым контуром питания, но расположена на расстоянии 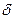 от его центра
от его центра 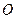 , то для расчета дебита такой скважины прибегают к методу отображения источников и стоков, который заключается в отображении реальной скважины-стока
, то для расчета дебита такой скважины прибегают к методу отображения источников и стоков, который заключается в отображении реальной скважины-стока  в фиктивную скважину-источник
в фиктивную скважину-источник  , расположенную от первой на некотором расстоянии
, расположенную от первой на некотором расстоянии  и лежащую на продолжении линии
и лежащую на продолжении линии  , что проиллюстрировано на рисунке 1.
, что проиллюстрировано на рисунке 1.
|
|
|

|
| Рисунок 1 – Схема притока жидкости к скважине, эксцентрично расположенной в круговом пласте |
Расстояние  определим из условия постоянства потенциалов на контуре и, следовательно, в точках
определим из условия постоянства потенциалов на контуре и, следовательно, в точках  и
и  , которые согласно принципу суперпозиции и формуле (9) будут определяться следующим образом:
, которые согласно принципу суперпозиции и формуле (9) будут определяться следующим образом:
|
|  (10 (10
|
|
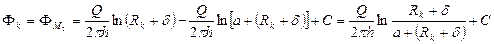 (11) (11)
|
|
 ,
,
откуда
 . (12) . (12)
|
|
Для того чтобы определить дебит скважины  , определим потенциал на её забое:
, определим потенциал на её забое:
 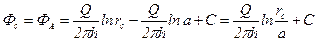 . (13) . (13)
|
|
Вычитая из равенства (10) соотношение (13) с учётом выражения (12), получим
 .(14) .(14)
|
|
Из выражений (7) и (14) получим окончательную формулу для расчёта дебита скважины, эксцентрично расположенной в круговом пласте, для случая плоского установившегося фильтрационного потока, то есть при  :
:
 . (15) . (15)
|
|
Следует заметить, что при эксцентриситете, равном нулю, выражение (15) обращается в формулу Дюпюи (5) [6, с.468-469].
Используя формулу (15), рассчитаем дебиты одиночной скважины для различных вариантов её расположения в круговом пласте. Результаты расчётов представим в численной и графической форме (рисунок 2):





| Рисунок 2 – График зависимости дебита скважины, эксцентрично расположенной в круговом пласте, от эксцентриситета, то есть расстояния от центра скважины до центра кругового пласта для случая гидродинамически совершенной скважины |
С поправкой на гидродинамическое несовершенство скважины рассчитаем её фактический дебит по формуле (1):
 ;
;
 ;
;
 ;
;
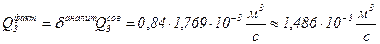 .
.
Для определения фильтрационных характеристик пласта определим коэффициент продуктивности скважины  , представляющий отношение дебита скважины
, представляющий отношение дебита скважины 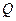 к перепаду давления
к перепаду давления  , то есть депрессии на пласт [4, с.9]:
, то есть депрессии на пласт [4, с.9]:
|
|
|
 , (16) , (16)
|
|
 ;
;
 ;
;
 ;
;
 .
.
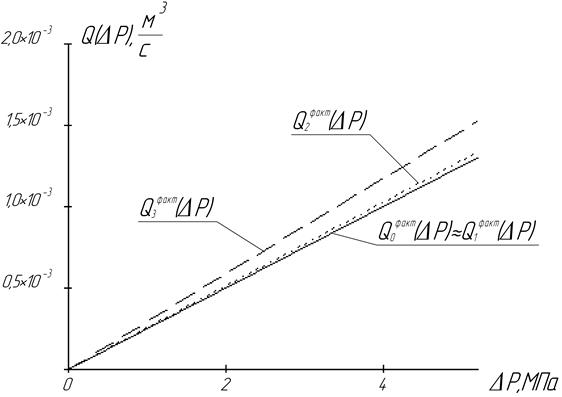
По результатам расчёта коэффициентов продуктивности построим индикаторные линии, то есть графики зависимостей расхода от разности давлений на контуре питания и галерее для различных вариантов расположения скважины в пласте, которые в пределах закона Дарси представляют прямые линии (рисунок 3).
|
| Рисунок 3 – Индикаторные линии плоскорадиального потока несжимаемой жидкости по закону Дарси |
2.2 Проверка применимости закона Дарси.
В ряде случаев линейность связи между скоростью фильтрации и градиентом давления нарушается, что наблюдается как при высоких скоростях, то есть турбулентном режиме фильтрации, так и при низких скоростях, то есть структурном режиме. Таким образом, можно выделить верхнюю и нижнюю границы применимости закона Дарси и соответствующие им две основные группы причин. Верхняя граница определяется группой причин, связанных с проявлением инерционных сил при достаточно высоких скоростях фильтрации, и связывается с некоторым критическим значением числа Рейнольдса, определяемого по следующей формуле:
|
|
|
 , (17) , (17)
|
|
где 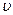 – скорость фильтрации,
– скорость фильтрации,  ;
;
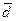 – некоторый характерный линейный размер поровых каналов;
– некоторый характерный линейный размер поровых каналов;
 – динамический коэффициент вязкости флюида,
– динамический коэффициент вязкости флюида,  .
.
Линейный параметр поровых каналов может быть определён одним из следующих способов:
§ по В.Н. Щелкачёву:
 ; (18) ; (18)
|
|
§ по М.Д. Миллионщикову:
 ; (19) ; (19)
|
|
где  – коэффициент проницаемости пористой среды,
– коэффициент проницаемости пористой среды,  ;
;
 – коэффициент пористости;
– коэффициент пористости;
 – критическое значение числа Рейнольдса, за пределами верхней границы которого фильтрация становится неламинарной и линейный закон фильтрации Дарси становится неприменим.
– критическое значение числа Рейнольдса, за пределами верхней границы которого фильтрация становится неламинарной и линейный закон фильтрации Дарси становится неприменим.
Нижняя граница определяется проявлением неньютоновских реологических свойств жидкости: её взаимодействием с твердым скелетом пористой среды при достаточно малых скоростях фильтрации [3, с.18-19, 22].
На основе вышеизложенного по формулам (17), (18) и (19) определим применимость закона Дарси для фильтрации нефти в скважину при её расположении, обеспечивающем максимальный дебит:
 ;
;
§ по В.Н. Щелкачёву:
 ;
;
 ;
;
§ по М.Д. Миллионщикову:
 ;
;
 .
.
Рассчитанные значения чисел Рейнольдса не выходят за верхнюю границу критического значения для такого эксцентричного расположения скважины, которое обеспечивает максимальную скорость фильтрации, следовательно, закон Дарси будет выполняться и для других вариантов расположения скважины в круговом пласте, рассмотренных выше.
Дата добавления: 2019-01-14; просмотров: 844; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
