Приближенный динамический расчет упругих систем с распределенными параметрами
Суть приближенных способов динамического расчета упругих систем заключается в том, чтобы систему с распределенными массами или систему с большим количеством сосредоточенных масс заменить эквивалентной одномассовой системой, а затем использовать формулу динамического коэффициента
 (12.3)
(12.3)
при колебаниях, или
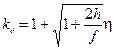 (12.4)
(12.4)
при ударе.
Известны различные методы приближенного вычисления частоты основного тона колебаний систем с распределенными параметрами, но ограничимся лишь наиболее популярным способом приведения масс.
 В этом способе заданная система с распределенной по любому закону массой m(z) (рис.12.2а) заменяется условной системой с одной приведенной массой Мп при условии, чтобы частота колебаний условной системы была равна частоте первого тона колебаний заданной системы. Две системы считаются динамически эквивалентными, если их кинетические энергии одинаковы.
В этом способе заданная система с распределенной по любому закону массой m(z) (рис.12.2а) заменяется условной системой с одной приведенной массой Мп при условии, чтобы частота колебаний условной системы была равна частоте первого тона колебаний заданной системы. Две системы считаются динамически эквивалентными, если их кинетические энергии одинаковы.
Для вычисления кинетической энергии нужно знать скорость движения сечений v(z,t)=dy(z,t)/dt. Так как при колебаниях упругих систем с распределенными параметрами функцию перемещений можно представить в виде произведения двух функций y(z,t)=y(z)T(t), то скорость движения сечений будет определяться уравнением.
 .
.
Кинетическая энергия заданной системы
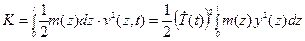 .
.
Кинетическая энергия эквивалентной системы (рис. 12.2, б)
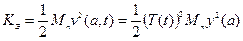 .
.
Из равенства этих энергий К=КЭ находим приведенную массу
 . (12.5)
. (12.5)
При наличии сосредоточенных масс эта формула примет вид
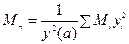 . (12.6)
. (12.6)
В этом способе уравнением изогнутой оси балки (или уравнением осевых перемещений при продольных колебаниях, и уравнением углов закручивания при крутильных колебаниях) нужно задаваться так, чтобы оно соответствовала условиям закрепления балки (стержня) на опорах. Это значит, что в случае поперечных колебаний уравнения перемещений y(z), углов поворота 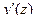 и кривизна
и кривизна 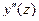 должны соответствовать типу опорных устройств.
должны соответствовать типу опорных устройств.
Собственные колебания упругих систем
Вычислив по формулам (12.5) и (12.6) или используя их совместно, получим приведенную массу, после чего определяется частота собственных колебаний невесомой системы с массой Мп,
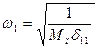 , (12.7)
, (12.7)
которая приближённо равна частоте первого тона колебаний заданной системы.
 Пример 12.2. Найти приближенно частоту первого тона колебаний жестко защемленной балки (рис. 12.3).
Пример 12.2. Найти приближенно частоту первого тона колебаний жестко защемленной балки (рис. 12.3).
Решение.
Вариант 1. Уравнения изогнутой оси балки и углов поворота найдем с помощью метода начальных параметров, приложив к невесомой балке силу P посередине пролёта (рис. 12.3, а).
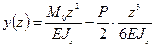 ,
, 
Из условия 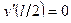 находим М0=Pl/8. Следовательно, уравнение изогнутой оси балки примет вид:
находим М0=Pl/8. Следовательно, уравнение изогнутой оси балки примет вид:

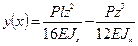 .
.
Так как при z=l/2 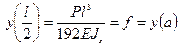 , то уравнение изогнутой оси можно записать так
, то уравнение изогнутой оси можно записать так
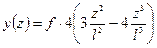 .
.
Приводим массу к середине пролёта балки, где 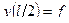 . Согласно (12.5) находим приведенную массу.
. Согласно (12.5) находим приведенную массу.
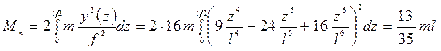 .
.
Частоту первого тона колебаний находим по формуле (12.7):
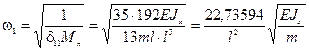 ,
,
что отличается от точного значения  на 1,62%.
на 1,62%.
Чтобы получить точное значение первой частоты, коэффициент приведения массы должен быть равен:
 .
.
Вариант 2. Для получения уравнения y(z) используем метод начальных параметров при продольно-поперечном изгибе (рис. 12.3б), приложив к балке критическую силу N. Учитывая, что 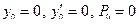 , это уравнение будет выглядеть так:
, это уравнение будет выглядеть так:
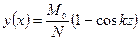 .
.
Из условия 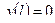 получим трансцендентное уравнение
получим трансцендентное уравнение  откуда
откуда 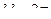 и уравнение изогнутой оси приобретает вид:
и уравнение изогнутой оси приобретает вид:
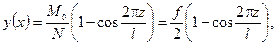
По формуле (12.6) получаем приведенную массу
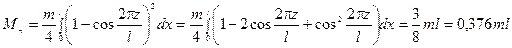 .
.
Частота собственных колебаний условной балки (12.7)
 отличается от точной всего на 1,14%.
отличается от точной всего на 1,14%.
 Пример 12.3. Найти приближенное значение частоты первого тона свободных колебаний балки с упруго-податливой заделкой с жесткостью c (рис. 12.4).
Пример 12.3. Найти приближенное значение частоты первого тона свободных колебаний балки с упруго-податливой заделкой с жесткостью c (рис. 12.4).
Решение.
Для получения уравнения y(z) приложим силу P на конце консоли и запишем уравнения метода начальных параметров (при М0=0 и Р0=Р):
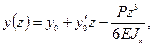
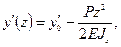
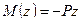 .
.
Из условий y(l)=0,  находим
находим 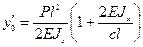 ,
, 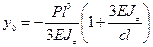 .
.
Уравнение изогнутой оси балки принимает вид:
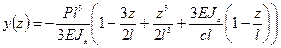 .
.
Рассмотрим случай, когда 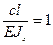 , тогда
, тогда 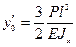 ,
, 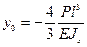 и уравнение изогнутой оси будет таким:
и уравнение изогнутой оси будет таким:

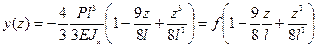 .
.
Подставляя это уравнение в (12.5), находим приведённую массу:
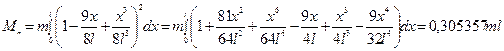 .
.
Приближенное значение частоты первого тона колебаний 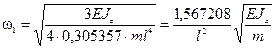 , что с погрешностью 0,64% отличается от точного значения.
, что с погрешностью 0,64% отличается от точного значения.
Дата добавления: 2018-11-24; просмотров: 268; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
