Модуль 10. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Общие понятия
Под сложным сопротивлением обычно понимают различные комбинации уже известных нам простых видов загружений (растяжения-сжатия, изгиба, кручения и т.д.), в результате чего в поперечном сечении элемента одновременно действует несколько силовых факторов.
Использование принципа независимости действия сил, позволяет получить для этого случая результирующие напряжения, перемещения, определяемые путем суммирования напряжений, перемещений, возникающих от внутренних усилий (N, Qx, Qy, Mкр, Mx, My), соответствующих простым деформациям растяжения (сжатия), сдвига, кручения, изгиба, возникающих при загружении стержня произвольной нагрузкой.
Следует заметить, что подобный подход, основанный на использовании принципа суперпозиции применим при рассмотрении достаточно жестких стержней, для которых справедливы линейные зависимости между деформациями и напряжениями
Наиболее распространенными комбинациями сложного сопротивления являются косой (неплоский) изгиб, изгиб с растяжением (сжатием), внецентренное растяжение (сжатие), изгиб с кручением, которые мы и рассмотрим ниже.
Сложный (неплоский) изгиб
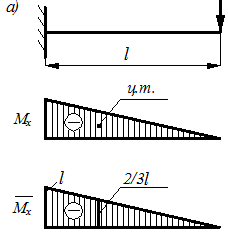
Сложный или неплоский изгиб возникает в том случае, когда равнодействующая внешних сил (т.е. результат действия внешних сил, располагающихся в различных плоскостях и проходящих через продольную ось балки), действует под углом к главным осям инерции сечения (рис. 10.1.а). В отличие от плоского изгиба, изогнутая ось балки в этом случае является не плоской кривой.
|
|
|
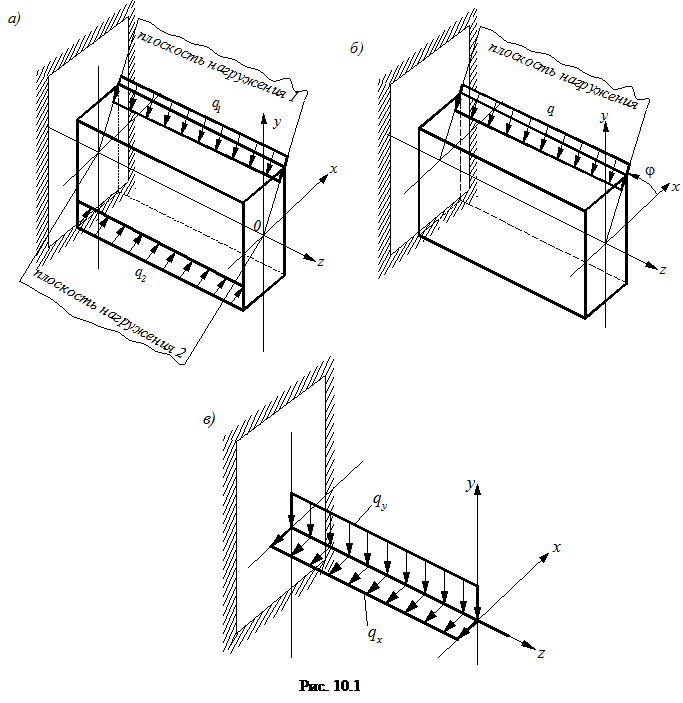
Частным случаем сложного изгиба является косой изгиб (рис. 10.1б), при котором все нагрузки, вызывающие изгиб, действуют в одной плоскости, не совпадающей ни с одной из главных плоскостей.
Примером конструкций, подвергающихся косому изгибу, могут служить кровельные прогоны (обрешетка кровли), когда вертикальная нагрузка от веса кровли и собственного веса прогона действует под углом к главной оси сечения.
Так же косой изгиб могут испытывать несимметричные сечения. В качестве примера может служить балочный элемент, выполненный из уголкового профиля, у которого одна из полок расположена параллельно основанию. Поскольку для него вертикальная нагрузка от собственного веса будет действовать под углом к главным осям инерции сечения, то этот элемент также будет испытывать косой изгиб.
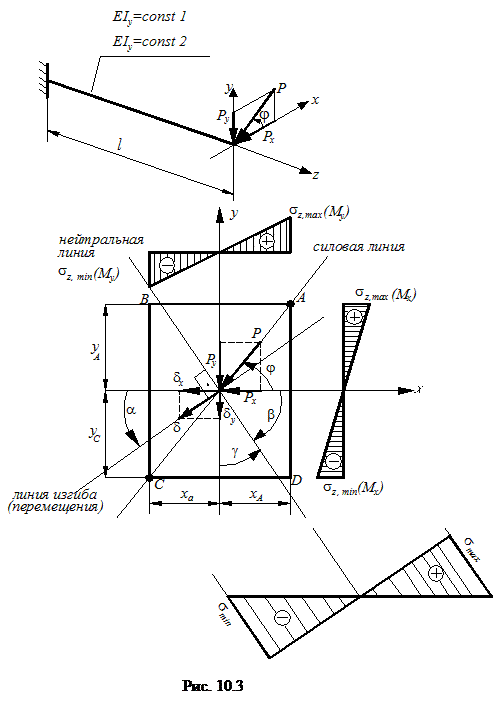
Использование указанных выше общих гипотез позволяет рассмотреть сложный (косой) изгиб как сумму двух плоских изгибов, действующих в плоскостях zoy и zox. В связи с этим нагрузки, действующие в произвольных плоскостях, раскладываются на две составляющие, лежащие в главных плоскостях zoy и zox (рис. 10.3)
|
|
|
Px = P cos φ, Py = P sin φ
Возникающие в поперечном сечении стержня соответствующие изгибающие моменты
Mx = Py·z = P·z sin φ
My = P·z cos φ
действуют одновременно и вызывают в произвольной точке любого сечения результирующие напряжения (см. рис.10.2а).
σz =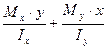 
(10.1)
Примечание: за положительные принимаются изгибающие моменты Mx и My, вызывающие растяжение в любой точке, располагающейся в 1-м квадранте системы координат xoy (рис. 10.2а).
Обозначим соотношение величин изгибающих моментов Mx и My, возникающих в сечении, через ctg φ
ctg φ =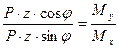 
(10.2)
 |
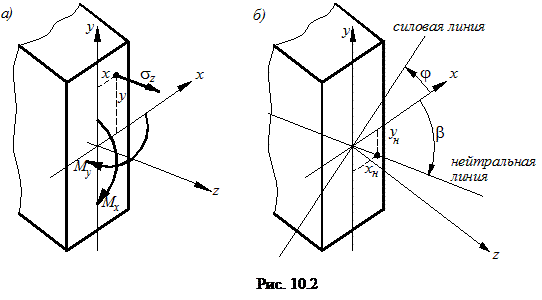При этом следует четко различать определения, часто используемые при рассмотрении данного раздела, а именно:
- силовой линии - след плоскости действия нагрузки при косом изгибе на поперечном сечении стержня;
- нейтральной линии- геометрическое место точек, в которых действующие напряжения σz=0.
Поскольку результатом действия обоих внутренних усилий Mx и My являются нормальные напряжения σz, появляется возможность суммировать эти величины
|
|
|
σ =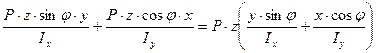 
(10.3)
Для точек, находящихся на нейтральной линии, нормальные напряжения σ, вычисляемые по формуле (10.3) будут равны нулю. Но, так как по условию задачи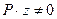 
, то нулю для выполнения этого условия нулю должно равняться выражение в скобках, то есть
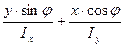= 0 (10.4)
Положение нейтральной линии определяется тангенсом угла наклона этой прямой, проходящей через начало осей координат (рис. 10.2б). Разрешив уравнение (10.4) относительно отношения yн/xн (здесь yн и xн – координаты точки, лежащей на нейтральной оси), получим
tg β =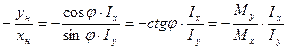 
tg β =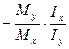 
- уравнение нейтральной линии (10.5)
Из рис. 10.3 видно, что tg β = ctg γ. Так как углы φ и γ откладываются от взаимно перпендикулярных осей х и у, то равными они могут быть лишь при выполнении условия Ix = Iy. Анализируя выражение (10.5) и приведенное утверждение можно прийти к 2-м важным выводам:
1. В общем случае при Ix ≠ Iy β + φ ≠ 900,то есть силовая линия и нейтральная линия не ортогональны.
2. Так как при косом изгибе отношение My / Mx = ctg φ постоянно по всей длине стержня, то и угол наклона нейтральной линии β также постоянен по всей длине стержня, а упругая линия деформированного стержня располагается в одной плоскости – плоскости изгиба.
|
|
|
Проверка прочности при сложном (косом) изгибе осуществляется на основе использования формулы (10.1). При этом максимальные напряжения возникают в точках А и С, наиболее удаленных от нейтральной линии (рис. 10.3, где эпюры σz(Mx) и σz(My) построены по граням сечения).
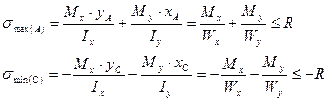(10.6)
где Wx = Ix / yA = Ix / yC , Wy = Iy / xA = Iy / xC , - максимальные значения моментов сопротивления сечения, вычисленные для наиболее растянутой (А) и наиболее сжатой (С) точек сечения, вычисленные относительно главных осей сечения х и у соответственно.
Перемещения, как и напряжения, определяются на основе использования принципа независимости действия сил. В любом сечении величина полного прогиба определяется суммированием его проекций
δ =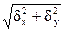 
(10.7)
где δx и δy – проекции полного прогиба d, определяемые на основе использования методов теории перемещения.
 |
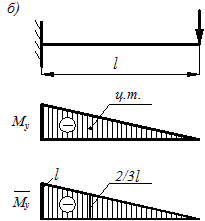
Направление полного перемещения найдем из рассмотрения примера №1 (рис. 10.4), где перемещения определяются на основе использования правила Верещагина.
Пример №10.1. Определить полное перемещение точки В от илы Р, приложенной под углом к горизонтали.
Разложим силу Р на две составляющих в вертикальной горизонтальной плоскости. Построив соответствующие грузовые и единичные эпюры, найдем перемещения по вертикали и горизонтали.
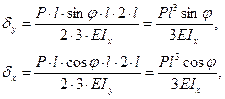(10.8)
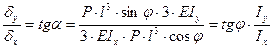(10.9)
Если принять во внимание, что
tg α·tg β =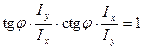 
,
то α + β = 900 (рис.10.3). Следовательно, нейтральная линия и направление перемещения ортогональны, а направление действия нагрузки не совпадает с направлением перемещения, что является весьма важной особенностью и определяет само название явления - косой изгиб.
| Py = P·sin φ
Mx,max = Pl·sin φ
| |||
|
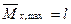
Px = P·cos φ
My,max = Pl·cosφ
|
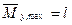
Рис. 10.4.
Дата добавления: 2018-11-24; просмотров: 489; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!