Формула О. Мора по определению перемещений в плоских упругих системах

 

Рассмотрим два состояния упругой системы. В первом состоянии действует заданная нагрузка. Это состояние называется действительным или грузовым (рис. 9.13а). В этом состоянии некоторая точка «к» получила перемещение Δ₂₁. Во втором состоянии действует по направлению перемещения Δ₂₁ единичная сила. Это состояние называется единичным (рис. 9.13б). Воспользуемся теоремой о взаимности работ Бетти (9.7), согласно которой:

                                                          Р₂Δ₂₁=Р₁Δ₁₂.                                              (а)

 

В нашем случае сила во втором состоянии Р₂=1. Тогда левая часть равенства (а) представляет собой возможную работу силы второго состояния на перемещении, вызванном силами первого состояния: Р₂Δ₂₁=1ּΔ₂₁=Δ_21, то есть равна перемещению точки упругой системы Δ₂₁ по направлению единичной силы от действия заданной нагрузки. Правую часть равенства (а), представляющую собой возможную работу сил первого состояния на перемещениях по их направлению, вызванных действием сил второго (единичного) состояния, выразим через соответствующие внутренние усилия. С этой целью в грузовом и единичном состояниях выделим элементарный отрезок ds упругой системы (рис. 9.14а, б) и покажем внутренние усилия, действующие на него. Внутренние усилия (рис. 9.14а) грузового состояния, снабжены индексом р (Nр, Mр, Qр) совершают работу на перемещениях, вызванных внутренними усилиями единичного состояния снабжены черточкой , , .

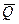Работа продольных сил Nр на перемещении Δds будет: . С учетом закона Гука можно записать

 

Работа продольных сил N_p на некотором участке упругой системы длиной l_i составит:

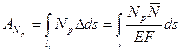                                                                                (б)

Работа изгибающего момента Мр на перемещении dφ будет: . С учетом закона Гука можно записать

                                                                                 (в)

Работа изгибающих моментов М_p на некотором участке упругой системы длиной l_i составит:

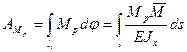                                                                              (г)

Поскольку поперечные силы Qр по высоте сечения распределены неравномерно, то работа на перемещении γds будет: . С учетом закона Гука . Но по формуле Журавского касательные напряжения

                                                                           (д)

С учетом формул (д) получаем:

                                                                          (е)

Введем обозначение:

                                                                                      (ж)

Формулу (е) можно переписать так:

                                                                                                 (з)

Тогда работа поперечных сил Q_p на некотором участке l_i составит:

                                                                                                (и)

Учитывая, что упругая система может состоять из нескольких участков, с учетом формул (б), (г), (и), а также равенства (а) запишем формулу Морав окончательном виде:

                                     (9.10)

Формула О. Мора в виде (9.10) применяется редко. В элементах конструкций, работающих преимущественно на растяжение или сжатие (например, элементы ферм), используется формула из одного слагаемого:

                                                                                  (9.11)

В конструктивных элементах типа балок, рам также применяется одночленная формула:

                                                                                 (9.12)

Следует заметить, что величины Nр, Mр, Qр, , , .представляют собой внутренние усилия текущих сечениях одноименных участков упругой системы, то есть являются функциями координаты s.

Последний интеграл формулы (9.10) из-за незначительного влияния поперечных сил на величины перемещений в практических расчетах не используется.

Рассмотрим примеры определения перемещений в некоторых упругих системах.

Пример № 9.5.Определить прогиб и угол поворота сечения «к» балки, постоянной изгибной жесткости EJ_x (рис. 9.15).

1). Реакции опор: А=⅜ql, B=⅛ ql.

2) Чтобы воспользоваться формулой О. Мора вида (9.12) для определения прогиба в точке «к» выберем единичное состояние, в котором в точке «к» по направлению искомого прогиба приложим силу равную единице (рис. 9.15б).

3) Запишем уравнения изгибающих моментов для каждого участка балки для грузового и единичного состояний:

 

, ;                              (а)

, .                                         (б)

Подставляя значения изгибающих моментов (а) и (б) в формулу (9.12), получаем:

.

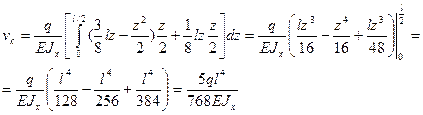4) Чтобы воспользоваться формулой О. Мора вида (9.12) для определения угла поворота сечения «к» выберем новое единичное состояние, в котором в точке «к» по направлению искомого угла поворота приложим момент равный единице (рис.9.15в). Уравнения моментов для каждого участка балки в этом единичном состоянии будут такими:

;                                            (в)

.

Таким образом:

,          .

Пример №9.6.Определить вертикальное, горизонтальное перемещения и угол поворота свободного конца консоли в виде четверти циркульной кривой (рис. 9.16) постоянной жесткости. При расчете влиянием продольных и поперечных сил пренебречь.

Для решения задачи по формуле Мора (9.12) воспользуемся полярными координатами.

1. Определение вертикального перемещения точки «к». По грузовому состоянию (рис. 9.16а) находим изгибающий момент:

 

;        .

Единичное состояние для определения вертикального перемещения показано на рис. 9.16б. Записываем уравнение изгибающего момента:

По формуле Мора получаем

.

 

После подстановке пределов интегрирования получаем:

Из единичного состояния для определения угла поворота сечения «к» (рис. 9.16в) изгибающий момент: .

.

Угол поворота

Аналогично можно получить горизонтальное перемещение Δ_гор, используя единичное состояние (рис. 9.16г):

 

---

Дата добавления: 2018-11-24; просмотров: 370; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!