ТЕМА 5. Информационные системы моделирования логистических бизнес-процессов, математический аппарат анализа и моделирования в логистике
1. Моделирование логистических информационных потоков, аналитические и имитационные модели в логистике
Одним из факторов, значительно повышающих эффективность работы ЛС является использование компьютерного моделирования, расчётной основой которого являются, как правило, именно математические, чаще всего разрешаемые при помощи численных, модели.
Метод моделирования основывается на принципе аналогии – возможности изучения реального объекта не непосредственно, а через рассмотрение подобного ему и более доступного объекта, его модели.
При этом под моделью будем понимать образ реальной логистической системы (ЛС) или процесса в материальной или абстрактной форме (т.е. описанный знаковыми средствами), отражающий существенные свойства моделируемого объекта (процесса) и замещающий его в ходе исследования и управления.
Моделирование даёт возможность проведения исследования без вмешательства в функционирование ЛС, например, определение предельно допустимых значений объемов материальных потоков и других параметров ЛС без риска разрушения моделируемой системы и соответствующих материальных последствий.
Поэтому практическими задачами моделирования ЛС являются: анализ логистических процессов (ЛП); прогнозирование; управление информационными потоками и выработка управленческих решений на всех уровнях иерархии ЛС.
Соответственно, важнейшими понятиями при моделировании являются
─ адекватность модели,
─ полезность модели,
─ точность отражения характерных черт объекта моделирования.
В современных экономических условиях часто эффективнее всего оказывается для выработки рациональных решений использовать численные модели, построенные на базе математических при поддержке вычислительных, коммуникационных и графических средств ИКТ.
Напомним, что математическое моделирование бывает
─ аналитическое и
─ имитационное.
Сущность аналитического моделирования
При аналитическом моделированиипроцессы функционирования элементов системы записываются в виде алгебраических, интегральных, дифференциальных, конечно-разностных и иных соотношений и логических условий. Результаты исследования аналитической модели могут быть:
─ качественными (устанавливаются такие свойства решения, как существование, единственность, устойчивость в большом и малом, характер зависимости выходных параметров от входных и т.п.);
─ аналитическими (устанавливаются явные зависимости для искомых характеристик);
─ численными (определяются числовые значения выходных величин для заданных входных данных, например, среднее время ожидания в очереди в модели СМО).
Существует класс объектов, для которых по различным причинам не разработаны аналитические модели, либо не разработаны методы решения полученной модели. В этом случае математическая модель заменяется имитатором или имитационной моделью.
Сущность имитационного моделирования
Имитационное моделирование – это метод исследования, при котором изучаемая система заменяется моделью, с достаточной точностью, описывающей реальную систему и с ней проводятся эксперименты с целью получения информации об исследуемой логистической системе.
Подобно физическому эксперименту, результаты каждого шага моделирования могут интерпретироваться как состояние системы в определенный момент времени, а метод моделирования может быть определен как наблюдение за динамикой изменения характеристик системы.
Имитационная модель – логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.
Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между ее элементами – разработке симулятора исследуемой предметной области для проведения различных экспериментов.
Естественно к имитационным моделям при их построении предъявляется и целый требований, одними из основных требований и универсальными относительно типа модели и объекта моделирования являются следующие: модель должна
─ учитывать все важные факторы, от которых существенно зависит исход операции;
─ быть достаточно простой для установления зависимостей между входящими в неё параметрами (не должна быть «засорена» множеством мелких, второстепенных факторов, учёт которых усложняет математический анализ и не оказывает значимого влияния на исследуемое явление.
Кроме того, при анализе сущности информации важно избежать двух крайних точек зрения:
1. Информация, как объективное свойство ЛС, рассматриваются в отрыве от других свойств этой системы (от организации, управления и т.п.).
2. Информация напрямую отождествляется со знанием, опытом, сведениями субъекта.
С одной стороны, информация осознана современным обществом как необходимое условие прогресса и наибольший экономический успех сегодня, как правило, сопутствует тем предприятиям, которые активно используют современные средства коммуникаций, ИТ и их приложения.
Однако, с другой стороны, разнородные информационные потоки необходимо упорядочить и проанализировать, для того чтобы на основе полученных данных принять рациональное решение.
Соответственно, очевидно, что разработка современного симулятора не представляется возможной без использования средств информационно-коммуникационных технологий и информационных систем.
В логистике используются два метода моделирования:
─ метод Монте-Карло (метод статистических испытаний);
─ метод имитационного моделирования (статистическое моделирование).
К имитационному моделированию прибегают, когда: дорого или невозможно экспериментировать на реальном объекте; невозможно построить аналитическую модель: в системе есть время, причинные связи, последствия, нелинейности, стохастические (случайные) переменные; необходимо имитировать поведение системы во времени.
Области применения: логистика; бизнес процессы; производство; сервисные центры; цепочки поставок; рынок и конкуренция; управление проектами; ВПК; дорожное движение; ИТ-инфраструктура; динамика населения; уличное движение; экосистемы и т.д.
Применение имитационного моделирования в логистике: перевозка товаров от поставщиков до «первого» склада; перевозка товаров между складами системы распределения; перевозка товаров со складов системы распределения в пункты продажи; погрузка, разгрузка транспортного средства; отбор товара в зоне хранения склада и др.
Примеры систем имитационного моделирования: AnyLogic; Aimsun; Arena; eM-Plant; Powersim; GPSS; NS-2; Transyt.
2. Математический аппарат анализа и моделирования логистических информационных потоков. Классификация математических моделей и методов
Для того чтобы эффективно использовать существующие модели в управлении ИП и разрабатывать новые, необходима их классификация.
Модели делятся на два класса:

Рисунок 1
Изоморфные модели представляют собой почти полный эквивалент моделируемой системы и способны полностью заменить ее.
Гомоморфные модели представляют собой модели, подобные отображаемому объекту лишь в отношениях, характерных и важных для процесса моделирования (практически все модели, используемые в логистике, являются гомоморфными).
Модели, используемые в логистике, могут быть классифицированы по различным признакам, ограничимся одной из наиболее распространённых классификаций.

Рисунок 2
Материальные (физические) – это модели, воспроизводящие основные геометрические, физические, динамические и функциональные характеристики изучаемого объекта (макеты). Используются чаще всего при исследовании технических систем или систем управления. Основные недостатки: трудность построения и дороговизна.
В логистике преимущественно используются абстрактно-концептуальные модели, которые подразделяют на символьные и математические.
Символьные модели построены на основе различных, определенным образом организованных знаков, символов, кодов, слов или массивов чисел, изображающих исследуемый оригинал (характерная черта: используются специальным образом построенные словари (тезаурусы), в которых каждое слово имеет только одно определенное значение). Недостаток: информацию, полученную с помощью использования символьных моделей, неудобно обрабатывать для дальнейшего использования в системах логистического управления.
Наибольшее распространение в процессе создания и эксплуатации систем логистического управления получили математические модели. Математическое моделирование бывает аналитическое и имитационное.
Особенностью аналитических моделей является то, что закономерности строения и поведения объекта моделирования описываются точными аналитическими соотношениями.
Имитационная модель – это виртуальное (компьютерное) воспроизведение функционирования системы: ее перехода из одного состояния в другое, осуществляемое в соответствии с однозначно определенными операционными правилами (математическими зависимостями (уравнениями), алгоритмами и т.п.). На ЭВМ, как правило, имитируется течение управляемого процесса с последующим анализом результатов моделирования.
Имитационные модели широко применяются
─ для прогнозирования поведения ЛС,
─ при проектировании и размещении предприятий,
─ для обучения и тренировки персонала и т.д.
Составление математических моделей логистических и экономических процессов производится часто на основе экономико-математических методов, поэтому далее рассмотрим их классификацию.
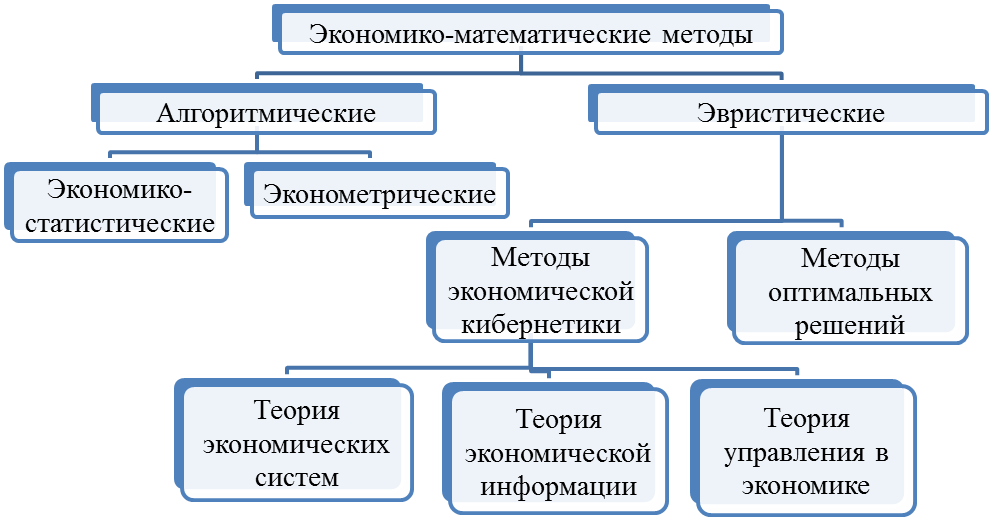
Рисунок 3
Алгоритмические методы позволяют реализовать модели, в которых устанавливают связи между входными и выходными параметрами описываемого компонента, скоростями их изменения и т.п.; в свою очередь эти методы разделяют на экономико-статистические и эконометрические.
Экономико-статистические используют описания характерных элементов, основанные на математической и экономической статистике.
Эконометрические базируются на математическом описании происходящих экономических процессов (например, общий фонд заработной платы однозначно математически связан с числом работающих и их распределением по разрядам).
Эвристические методы – набор типовых решений, обеспечивающих пусть и не оптимальную, по вполне работоспособную процедуру получения описаний, пригодных для дальнейшего построения моделей. Эвристические методы делятся на методы исследования операций и методы экономической кибернетики. Методы экономической кибернетики, в свою очередь, подразделяются на методы теории экономических систем и моделей, методы теории экономической информации и методы теории управляющих систем.
Визуализация результата модели производится при помощи специальных графических модулей и опций графической оболочки системы.
На рисунке 4 представлены объекты моделирования, для исследования которых применимы перечисленные методы моделирования (здесь детализация только для ЛС).

Рисунок 4 – Объекты моделирования
3. Этапы моделирования логистических процессов
Процесс моделирования, в том числе и моделирования процессов управления ИП, включает в себя три структурных элемента (см. рисунок 5): объект исследования; субъект (исследователь); модель, опосредующую отношения между познающим субъектом и познаваемым объектом (поэтому на схеме «модель» находится между первым и вторым элементами).
Проанализируем детально последовательность и содержание основных этапов моделирования, выделив следующие шесть этапов:
1. постановка экономико-логистической проблемы, ее качественный анализ;
2. построение математической модели;
3. математический анализ модели;
4. подготовка исходной информации;
5. численное решение;
6. анализ численных результатов и их применение.

Рисунок 5
Далее рассмотрим каждый из этапов более подробно.
1. Постановка экономико-логистической проблемы и ее качественный анализ. На этом этапе требуется сформулировать сущность проблемы, принимаемые предпосылки и допущения. Необходимо выделить важнейшие черты и свойства моделируемого объекта, изучить его структуру и взаимосвязь его элементов, хотя бы предварительно сформулировать гипотезы, объясняющие поведение и развитие объекта.
2. Построение математической модели. Это этап формализации экономической проблемы, т.е. выражения ее в виде конкретных математических зависимостей (функций, уравнений, неравенств и т.п.).
3. Математический анализ модели. На этом этапе чисто математическими приемами исследования выявляются общие свойства модели и ее решений. Однако модели сложных экономических объектов с большим трудом поддаются аналитическому исследованию; в таких случаях переходят к численным методам исследования.
4. Подготовка исходной информации. В реальных задачах это, как правило, наиболее трудоемкий этап моделирования.
5. Численное решение. Этот этап включает
─ разработку алгоритмов численного решения задачи,
─ подготовку программ на ЭВМ и
─ непосредственное проведение расчетов.
Численное решение существенно дополняет результаты аналитического исследования, а для многих моделей является единственно возможным.
6. Анализ численных результатов и их применение. На этом этапе, прежде всего, решается важнейший вопрос о правильности и полноте результатов моделирования и применимости их как в практической деятельности, так и в целях усовершенствования модели. Поэтому, в первую очередь, должна быть проведена проверка адекватности модели по тем свойствам, которые выбраны в качестве существенных. То есть необходима проверка правильности структуры (логики модели), и проверка соответствия данных, полученных на основе модели, реальному процессу.
Этапы моделирования находятся в тесной информационной взаимосвязи, в частности, могут иметь место возвратные информационные связи этапов.
В целом модели и теории, которые формулируются и решаются с помощью численных методов, представляют собой неотъемлемую составляющую диалога между теорией и практикой. В условиях быстро меняющихся постановок проблем, когда сегодняшние решения завтра уже не пригодны, требуются не только готовые к непосредственному использованию знания, но и умственная динамика, кругозор, компетентность, а также готовность постоянно критически оценивать свои знания.
Дата добавления: 2018-11-24; просмотров: 547; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
