Получение математических моделей в приложениях Mathcad и Excel

В приложении Mathcadможно записать формулы приведенного выше алгоритма и вычислить коэффициенты функциональной зависимости.

Существуют также и встроенные функции для определения математических моделей. Например, пусть имеются значения х и у, полученные в результате проведения опытов. Надо найти математическую модель в виде полинома второй степени:

y = a0 + a1 × x + a2 × x²

 Можно использовать для решения задачи встроенную функцию linfit. На листе Mathcadтогда нужно записать:

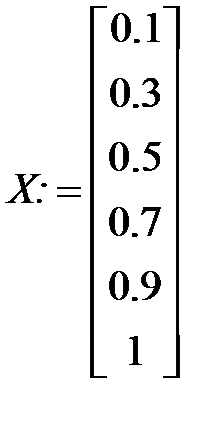
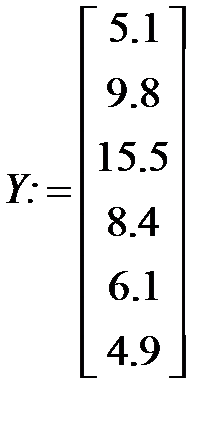
А:= linfit(Х, Y, F)

Вычисленные значения a 0, a 1, a 2 будут записаны в векторе А, который появится после ввода текста: A =

Для построения графика теперь можно определить значения:

         i :=0..5         t := 0, 0.01..1      Z(t) := F(t)*A

Здесь Z(t) − искомая математическая модель. Если  построить на одном графике зависимость Z(t) от t и зависимость Y _i от X _i, то можно сравнить, насколько хорошо полученный полином описывает данные опытов.

В приложении Excel предоставляется интересная возможность получения математических моделей через построение графиков функций.

Пусть имеются значения x ₁, x ₂, …, x_n и соответствующие им значения y ₁, y ₂, …, y _n. Надо для этих данных построить точечный график и выполнить команду Диаграмма/Добавить линию тренда. В появившемся окне на вкладке Тип определить вид математической модели, а на вкладке Параметры отметить флажок Показывать уравнение на диаграмме. После нажатия <О K > искомое уравнение появится на графике.

Модель многомерного объекта

Предположим, что технологический процесс можно описать математической моделью вида

y = b₀ + b₁×x₁ +…+ b_n×x_n + b₁₂×x₁×x₂ +…+ b_n–1,n×x_n–1×x_n,

где y – выходной параметр процесса; b ₀, b ₁, …, b_{n – 1, n} – искомые неизвестные коэффициенты процесса; x ₁, …, x_n – входные параметры процесса.

Соотношения такого вида называются уравнениями регрессии.

Например, для процесса (рис. 21.2), имеющего три входных параметра (фактора), математическая модель примет вид

y = b₀ + b₁ × x₁ + b₂ × x₂ + b₃ × x₃ + b₁₂ × x₁ × x₂ + b₁₃ × x₁ × x₃ + b₂₃ × x₂ × x₃.

Чтобы определить коэффициенты математической модели процесса необходимо провести эксперимент по соответствующему плану, например по плану полного факторного эксперимента.

Рис. 21.2. Многомерный объект

Количество опытов в эксперименте рассчитывается по формуле N = 2 ⁿ, где n – количество факторов. Входные воздействия принимают минимальные и максимальные значения. Для упрощения вычислений нужно перейти от физических переменных x ₁, …, x_n к кодированным по следующей формуле:

z_i  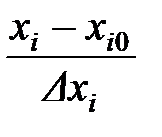= ,     i = 1, 2, 3.

Здесь x_i0 – значение фактора на базовом (нулевом) уровне, равное среднему значению между минимальным и максимальным значениями; ∆x_i  – интервал варьирования по данному фактору.

В случае трех входных параметров план проведения эксперимента имеет вид, представленный на рис. 21.3.

№ п/п z 1 z 2 z 3 уэ 1 –1 –1 –1 уэ1 2 +1 –1 –1 уэ 2 3 –1 +1 –1 уэ 3 4 +1 +1 –1 уэ 4 5 –1 –1 +1 уэ 5 6 +1 –1 +1 уэ 6 7 –1 +1 +1 уэ 7 8 +1 +1 +1 уэ8

Значение –1 соответствует минимальному значению входного параметра, +1 – максимальному значению входного параметра.

В соответствии с методом наименьших квадратов производится вычисление коэффициентов:

Рис. 10.3. План эксперимента

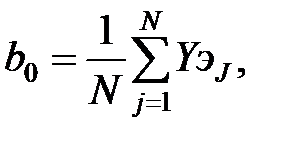
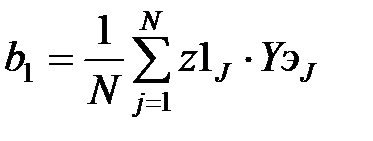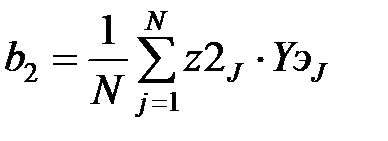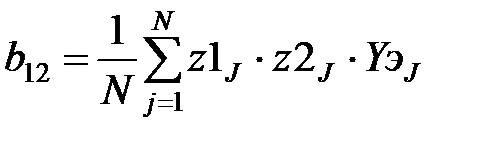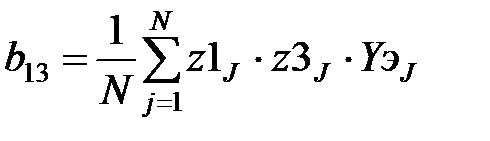, , , , , ,  i =1,2,…, N

Коэффициент регрессии b (b ₀, b ₁, …, b_{n – 1, n}.) считается значимым, если выполняется условие

,   ,

где Sb – среднеквадратичная ошибка в определении коэффициентов регрессии; t _Т – табличное значение критерия Стьюдента, которое выбирается для числа степеней свободы f1 = m – 1.

Для расчета дисперсии воспроизводимости нужно выполнить дополнительно m опытов (m < N) по любой строчке плана, например, при значениях входных факторов на базовом уровне.

В результате получаются дополнительные значения экспериментальных данных yd ₁,yd ₂, …, yd_m.

Тогда

Sy² = 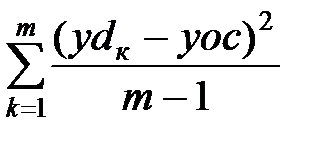 , yoc =  ,  k = 1, …, m.

 

В табл. 10.1 приведены значения критерия Стьюдента.

 

Таблица 10.1

Значения критерия Стьюдента

Число степеней свободы f1	1	2	3	4	5	6	7
Значение коэффициента	12.71	4.30	3.18	2.78	2.57	2.45	2.36

 

Если коэффициент не удовлетворяет критерию Стьюдента, то он считается незначимым и приравнивается к нулю.

Проверка адекватности (соответствия) полученного уравнения регрессии экспериментальным данным проводится с помощью критерия Фишера. Для этого вычисляются

,  F = ,

где 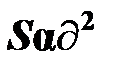– оценка дисперсии адекватности; B – число значимых коэффициентов уравнения регрессии; y э _j, y p_j – экспериментальное и рассчитанное по найденной математической модели значения y в j-м опыте.

Определяется также табличное значение критерия Фишера F _Т из табл. 21.2 по числу степеней свободы f 1 и числу  степеней  свободы  f 2 = N – B.

Если F < F _Т, то уравнение регрессии рассматривается как модель исследуемого процесса.

 

Таблица 10.2

Коэффициенты критерия Фишера

Число степеней свободы f1	Число степеней свободы f2
	1	2	3	4	5	6
1	161.40	199.50	215.70	224.60	320.20	234.00
2	18.51	19.00	19.16	19.25	19.30	19.33
3	10.13	9.55	9.28	9.12	9.01	8.94
4	7.71	6.94	6.59	6.39	6.26	6.16
5	6.61	5.79	5.41	5.19	5.05	4.95
6	5.99	5.14	4.76	4.53	3.39	4.28
7	5.99	4.74	4.35	4.12	3.97	3.97

 

Если полученное уравнение не адекватно процессу, то нужно перейти к более сложному виду математической модели, вновь провести опыты и обработать их результаты.

Если уравнение адекватно процессу, то нужно от кодированных переменных перейти к физическим.

МЕТОДЫ ОПТИМИЗАЦИИ

Задачу оптимизации в общем виде можно сформулировать так: определить значения входных параметров x ₁, x ₂, …, x _n некоторого процесса, которые обеспечивают максимум или минимум целевой функции f ( x ₁, x ₂, …, x_n ), характеризующей показатели процесса, и удовлетворяют ограничениям, если они присутствуют.

Метод сканирования

Рассмотрим использование метода сканирования на примере для оптимизации процесса, имеющего два входных параметра x ₁ , x ₂ и выходной параметр – y . Пусть требуется определить оптимальные значения x ₁ и x ₂, которые обеспечивали бы минимум целевой функции

y = f(x₁, x₂)

и удовлетворяли ограничениям:

a1 <= x₁ <= b1,   a2 <= x₂ <= b2

g(x₁, x₂) > 0

(последнее ограничение может отсутствовать).

Метод сканирования заключается в нахождении значений x ₁из интервала [ a 1, b 1] , начиная с a 1 и до b 1 с шагом h 1 и определении значений x ₂ из интервала [ a 2, b 2], начиная с a 2 и до b 2 с шагом h 2. Для всех значений x ₁ и x ₂, удовлетворяющих ограничениям g(x₁, x₂) > 0, нужно вычислить значения целевой функции y = f(x₁, x₂).

Те значения x ₁ и x ₂, для которых значение целевой функции минимально, являются искомым решением.

Рассмотрим алгоритм метода сканирования:

1. Ввод исходных данных: a 1, b 1, h 1, a 2, b 2, h 2инекоторого числаA, заведомо большего, чем значение целевой функции.

2. Вычисление yopt = A, x1opt = a1, x2opt = a2.

3. x₁ = a1

4. x₂ = a2

5. Проверка ограничения: если ограничение не выполняется, т. е. g(x₁, x₂) <= 0, то переход к п. 8, иначе – переход к следующему пункту.

6. Вычисление целевой функции y = f(x₁, x₂).

7. Если y < yopt, то yopt = y, x1opt = x₁, x2opt = x₂ , иначе – переход к следующему пункту.

8. Вычисление x₂ = x₂ + h2.

9. Если x₂ <= b2, то переход к п. 5, иначе – переход к следующему пункту.

10. Вычисление x₁ = x₁ + h1.

11. Если x₁ <= b1, то переход к п. 4, иначе – переход к следующему пункту.

12. Вывод оптимальных значений x 1 opt,x 2 opt и минимального значения целевой функции yopt.

Метод случайного поиска

Рассмотрим применение метода случайного поиска для оптимизации процесса на примере, приведенном выше. Идея метода основана на многократном (N раз) вычислении целевой функции y для значений x ₁ и x ₂, выбранных из отрезков [ a 1, b 1] и [ a 2, b 2] случайным образом. Те значения x ₁ и x ₂, при которых целевая функция минимальна и удовлетворяются ограничения и являются решением.

Для определения случайного числа x на отрезке [ a, b ] можно использовать встроенную функцию Rnd. Тогда x = ( b – a ) × Rnd(1) + a.

Алгоритм метода случайного поиска:

1. Ввод исходных данных: a 1, b 1, a 2, b 2,количества опытовNичислаA, заведомо большего, чем значение целевой функции.

2. Вычисление yopt = A, x1opt = a1, x2opt = a2.

3. i = 1.

4. Вычисление x₁ = (b1 – a1) × Rnd(1) + a1, x₂ = (b2 – a2) × Rnd(1) + + a2.

5. Проверка ограничения: если g(x₁, x₂) <= 0 , то переход к п. 8, иначе – переход к следующему пункту.

6. Вычисление целевой функции y = f(x₁, x₂).

7. Если y < yopt,то yopt = y, x1opt = x₁, x2opt = x₂, иначе – переход к следующему пункту.

8. i = i + 1.

9. Если i <= N, то переход к п. 4, иначе – переход к п. 10.

10. Вывод оптимальных значений x 1 opt, x 2 opt и минимального значения целевой функции yopt.

---

Дата добавления: 2018-11-24; просмотров: 264; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!