Приближенное вычисление интеграла в приложениях Mathcad и Excel

Чтобы вычислить определенный интеграл в приложении Mathcad нужно записать интеграл, подынтегральную функцию и пределы интегрирования. Например:

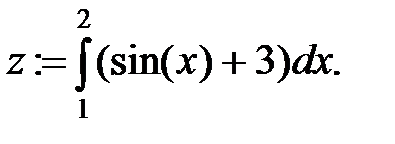
Для получения численного значения записывается выражение:

z =

Численные методы решения уравнений

Пусть имеется уравнение: f ( x ) = 0.                                             

Решение уравнения численными методами состоит из двух этапов:

- отделение корней, т.е. нахождение таких отрезков [ a,b ] на оси OX, внутри которых имеется один корень;

- вычисление корней с заданной точностью.

Одним из способов отделения корней является графический способ. Рассмотрим его на примере.

Пусть требуется отделить корни уравнения 3 – x – ln ( x ) = 0.

y = ln(x)

y = 3 – x

Перепишем исходное уравнение в виде 3 – x = ln ( x )и построим графики функций y = 3 – x и y = ln ( x )(рис. 19.3). Из чертежа видно, что графики пересекаются в единственной точке, абсцисса которой находится внутри отрезка [1, 3]. Знаки функции на концах отрезка разные: f (1) = 3 – 1 – ln (1) > 0, f(3) = 3 – 3 – ln (3) < 0. Значит, данное уравнение имеет один дей-ствительный корень, лежащий внутри отрезка [1, 3],т. е.a = 1, b = 3.

Можно также отделить корни, построив график функции f ( x )в приложении Mathcad или в приложении Excel.

После того, как определен отрезок (или отрезки), внутри которого имеется один корень, можно вычислить его с заданной точностью одним из методов.

Метод касательных. При использовании данного метода для вычисления корня уравнения необходимо определить начальное приближение корня x₀: x₀ = a, если знаки f(a) и f ¢¢(a ) совпадают, и x₀ = b, если знаки f(b) и f ¢¢(b) совпадают. Последовательные приближения корня рассчитываются по формуле

x_{n +1} = x_n – 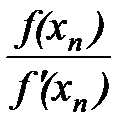, n = 0, 1 ,2, ….

Вычисления продолжаются до тех пор, пока не будет выполнено условие | x_{n + 1}  – x_n | <= e , где e – требуемая точность вычисления корня.

Рассмотрим алгоритм метода касательных:

1. Ввод значений a, b, e.

2. Вычисление начального приближения корня x_{n 1} = a, если

f ( a ) × f ¢¢ ( a ) > 0 или x_{n 1} = b в противном случае.

3. Вычисление x_n= x_{n 1}.

4. Определение очередного приближения корня по формуле

x_{n 1} = x_n –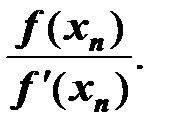

5. Если | x_{n 1}  – x_n | > e, то переход к пункту 3, в противном случае – переход к п. 6.

6. Вывод значения корня x_{n 1}.

Метод дихотомии (деления отрезка пополам).При использовании метода дихотомии отрезок [ a , b ] делится пополам. Из полученных двух отрезков для дальнейших вычислений выбирается тот, на концах которого функция f ( x ) имеет разные знаки. Выбранный отрезок вновь делится пополам. Вычисления продолжаются до тех пор, пока величина последнего из полученных отрезков не станет меньше 2 e.

Рассмотрим алгоритм метода дихотомии:

1. Ввод значений a, b, e.

2. Вычисление .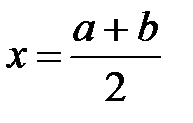

3. Если f ( x ) = 0, то переход к п. 6, иначе – переход к п. 4.

4. Если f ( x ) × f ( a ) <= 0,то b = x, иначе– a = x.

5. Если | a –b | > 2 e, то переход к п. 2, иначе – переход к следующему пункту.

6. Вывод значения корня x.

---

Дата добавления: 2018-11-24; просмотров: 204; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!