ФАКТОР ГРУППА ГРУППЫ ПО НОРМАЛЬНОМУ ДЕЛИТЕЛЮ.
Пусть дана для определенности мультипликативная группа G. И пусть подгруппа А её нормальный делитель.
Понятие нормального делителя группы дает возможность привести новый пример группы, а именно фактор - группы группы G по нормальному делителю А.
Рассмотрим разложение группы G по нормальному делителю А и запишем множество состоящее из различных смежных классов группы G по подгруппе А.
Обозначим это множество следующим образом G/А.
G/А={xА, yА,…}.
Покажем, что это множество само образует группу относительно операции определенной в G. Для этого нужно ввести операцию умножения классов и показать, что она является бинарной алгебраической операцией на данном множестве.
1.) "xА, yАÎG/А, xА⋅yА=xА⋅Аy=xАy=x⋅yА, где x⋅yÎG, «⋅» - Б.А.О.
Таким образом, чтобы перемножить 2 смежных класса нужно перемножить их образующие элементы.
2.) "xА, yА, zАÎG/А, (xА⋅yА)⋅zА= xyА⋅zА=xyzА.
xА⋅(yА⋅zА)= xА⋅yzА=xyzА⇨ «⋅» - ассоциативна.
3.) Так как еÎG, то еАÎ G/А, "xАÎG/А, xА⋅еА=x⋅еА=xА, еА=А.
4.) $ 
ÎG ⇨ $ АÎG/А, xА⋅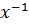 
А=(x⋅ 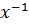)⋅А=еА=А, значит 
А обратный элемент для xА.
Таким образом, множество различных смежных классов группы G по нормальному делителю А само образует группу относительно заданной в G операции.
Её называют фактор группой группы G по нормальному делителю А.
ЯДРО ГОМОМОРФИЗМА ГРУПП.
Пусть дана для определенности мультипликативная группа G, и пусть она гомоморфна группе G¢, которая также для определенности мультипликативная.
|
|
|
Обозначим гомоморфизм групп G и G¢ через j.
Определение. Ядром гомоморфизма j группы G на группу G¢ называется множество всех тех элементов из G которые отображаются на нейтральный элемент группы G¢.
Обозначим kerj={x/xÎG, j(x)=1¢, 1¢ÎG¢}.
Теорема.
Ядро гомоморфизма j является нормальным делителем группы G.
Доказательство:
Пусть дан гомоморфизм j группы G на группу G¢ и пусть kerj - ядро гомоморфизма, чтобы доказать, что kerj - нормальный делитель группы G нужно сначала доказать, что kerj подгруппа группы G, а затем, используя критерий нормального делителя доказать, что kerj - нормальный делитель группы G.
I. Чтобы доказать, что kerj - подгруппа группы G воспользуемся критерием подгруппы:
1. "x, yÎkerj, j(x)=1¢, j(y)=1¢, где 1¢ÎG¢.
j(x⋅y)= j(x)⋅ j(y)= 1¢⋅1¢=1¢⇨так как j гомоморфизм⇨ x⋅yÎkerj.
2. "xÎkerj, j(x)=1¢, так как G – группа $ 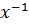ÎG, j( )= 
= 
=1¢⇨ Îkerj.
Выполнились оба требования критерия подгруппы⇨ kerj - подгруппа группы G.
II. "xÎkerj, j(x)=1¢, 1¢ÎG¢.
"yÎG, и составим элемент сопряженным с x.
⋅x⋅y.
Покажем, что 
⋅x⋅yÎkerj.
|
|
|
Найдем j( ⋅x⋅y)=j( 
)⋅j(x)⋅j(y)= так как j - гомоморфное = 
⋅1¢⋅j(y)= 1¢⋅1¢=1¢⇨ ⋅x⋅yÎkerj.
Таким образом ядро гомоморфизма j является нормальным делителем группы G.
Дата добавления: 2018-11-24; просмотров: 242; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!