СМЕЖНЫЕ КЛАССЫ И ИХ СВОЙСТВА.
Пусть дана для определенности – мультипликативная группа (G,∙), А – подгруппа группы G, А={ 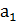 ,
, 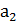 ,…,
,…, 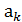 }.
}.
Возьмем "xÎG, и рассмотрим множество элементов вида x∙ 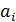 , i=
, i= 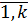 , x∙
, x∙ 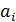 ÎG.
ÎG.
Полученное множество элементов называют смежным классом группы G по подгруппе А порожденным элементом x.
Так как x стоит слева, то это левый смежный класс.
Определение.
Левым смежным классом группы G по подгруппе А, порожденным элементом x называют множество элементов вида.
x∙А={ x∙  | xÎG,
| xÎG, 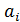 ÎА}.
ÎА}.
Аналогично определяется правый смежный класс.
А∙x={  ∙ x| xÎG,
∙ x| xÎG, 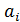 ÎА}.
ÎА}.
Заметим, что если операция в группе сложение, то левый смежный класс порожденный элементом x, имеет вид: x+А={ x+  | xÎG,
| xÎG, 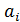 ÎА}.
ÎА}.
Аналогично правый смежный класс: А+x={  +x| xÎG,
+x| xÎG, 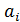 ÎА}.
ÎА}.
СВОЙСТВА СМЕЖНЫХ КЛАССОВ.
Доказательство будем проводить для левых смежных классов, для правых аналогично.
1. Сама подгруппа А является как левым, так и правым смежным классом группы G по подгруппе А.
Доказательство:
Действительно, для доказательства достаточно в качестве порождающего элемента выбрать еÎG, x=е, x∙А=e∙А= А∙е=А.
2. Порождающий элемент x принадлежит смежному классу x∙А.
Доказательство:
Действительно, так как А – подгруппа, значит А – группа, и еÎА, тогда x∙е=xÎА.
3. Любой смежный класс состоит из различных элементов группы G, и число этих элементов равно порядку подгруппы А.
Доказательство:
|
|
|
Пусть составлен смежный класс x∙А={x∙ 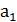 , x∙
, x∙ 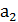 ,…, x∙
,…, x∙ 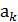 }.
}.
Предположим противное x∙  =x∙
=x∙ 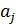 , так как xÎG, то $
, так как xÎG, то $ 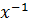 ÎG.
ÎG.
Умножим обе части последнего равенства на 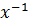 слева.
слева.
Получим, 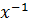 ∙( x∙
∙( x∙  )=
)= 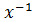 ∙ (x∙
∙ (x∙ 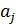 ),
),
( 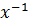 ∙x)∙
∙x)∙  =(
=( 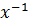 ∙ x)∙
∙ x)∙ 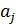 ,
,
1∙  =1∙
=1∙ 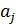 ,
,  =
= 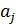 .
.
Пришли к противоречию, так как  ,
, 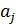 ÎА, а в группе все элементы различны между собой.
ÎА, а в группе все элементы различны между собой.
Противоречие получено в результате неверного предположения.
4. Любой левый смежный класс группы G по подгруппе А, вполне определяется любым из своих элементов, т.е. если:
yÎx⋅A⇨y⋅A=x⋅A.
Доказательство проведем методом включения:
Пусть yÎx⋅A⇨y=x⋅  ,
,  ÎА, возьмем "uÎy⋅A⇨u=y⋅
ÎА, возьмем "uÎy⋅A⇨u=y⋅ 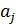 ,
, 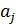 ÎА, так как
ÎА, так как
y= x⋅  ,то u=y⋅
,то u=y⋅ 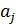 =(x⋅
=(x⋅  )⋅
)⋅ 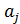 =x⋅(
=x⋅(  ⋅
⋅ 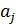 ), где
), где  ⋅
⋅ 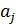 ÎА.
ÎА.
u=x⋅(  ⋅
⋅ 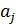 )⇨uÎx⋅A, y⋅AÍx⋅A.
)⇨uÎx⋅A, y⋅AÍx⋅A.
Пусть yÎx⋅A⇨y=x⋅  ,
,  ÎА.
ÎА.
Возьмем "vÎx⋅A⇨v= x⋅ 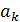 , где
, где 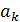 ÎА.
ÎА.
Рассмотрим y= x⋅  , так как
, так как  ÎА, А – группа, то $
ÎА, А – группа, то $ 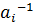 ÎА, умножим обе части последнего равенства на
ÎА, умножим обе части последнего равенства на 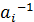 справа, получим
справа, получим
y⋅ 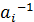 = (x⋅
= (x⋅  )⋅
)⋅ 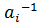 , y⋅
, y⋅ 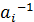 =x.
=x.
Получим, что x= y⋅ 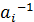 , тогда v= x⋅
, тогда v= x⋅ 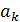 =(y⋅
=(y⋅ 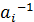 )⋅
)⋅ 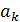 =y⋅(
=y⋅( 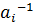 ⋅
⋅ 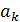 ), где
), где 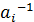 ⋅
⋅ 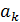 ÎА.
ÎА.
v=y⋅( 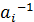 ⋅
⋅ 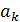 )⇨vÎy⋅A, так как выполнились оба включения, то y⋅A= x⋅A.
)⇨vÎy⋅A, так как выполнились оба включения, то y⋅A= x⋅A.
Ч.т.д.
5. Различные смежные классы не пересекаются между собой.
|
|
|
Доказательство: (метод от противного)
Пусть 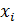 A и
A и 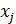 A различные смежные классы и пусть
A различные смежные классы и пусть 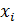 AÇ
AÇ 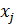 A¹Æ и пусть zÎ
A¹Æ и пусть zÎ 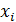 AÇ
AÇ 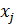 A⇨ zÎ
A⇨ zÎ 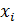 A и zÎ
A и zÎ 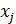 A, так как zÎ
A, так как zÎ 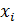 A⇨z⋅А=
A⇨z⋅А= 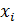 A ⇨
A ⇨ 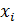 A=
A= 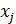 A.
A.
Если два смежных класса имеют хотя бы один общий элемент, то они совпадают, в противном случае классы не пересекаются.
6. Так как смежные классы составлялись с помощью каждого элемента группы G и совпавшие классы считают за один класс, то объединение различных, то есть не пересекающихся левых смежных классов, составляет всю группу G, аналогично для правых смежных классов.
Доказательство: G= 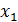 AÈ
AÈ 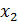 AÈ… - левосторонне разложение группы G по подгруппе А.
AÈ… - левосторонне разложение группы G по подгруппе А.
Если количество различных между собой классов различно, то левосторонне разложение имеет вид:
G= 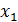 АÈ
АÈ 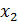 АÈ…È
АÈ…È 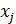 А, тогда индекс j – индекс разложения.
А, тогда индекс j – индекс разложения.
Аналогично, G=А 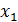 ÈА
ÈА 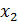 È…ÈА
È…ÈА 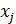 – правосторонние смежные классы.
– правосторонние смежные классы.
Дата добавления: 2018-11-24; просмотров: 578; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
